第三章 线性模型
线性模型目的:学得一个通过属性的线性组合来进行预测的函数。
一、对于回归任务
(一)一元线性回归
目的是学得如下函数:

在参数估计过程中,利用最小二乘估计确定 w 和 b 。(也是性能度量:均方误差最小化原理。)
(二)多元线性回归

这里x是d维向量,代表样本中有d个属性,拟合多元线性回归模型,预测 y 值。参数估计也是利用最小二乘估计思想。
注1:当设计矩阵X 对应的X’X不是满秩矩阵(比如属性个数远多于样本数时),参数w会有多个解满足均方误差最小化,此时常采用引入正则化项的方法来确定输出解。
注2:通过对输出标记 y 的变换,可以将线性回归模型与非线性回归模型相互转换,比如对数线性回归。
注3:在进行回归建模时,要注意各个属性之间是否存在多重复共线性,可以条件数K 来很衡量复共线性的程度 。当存在复共线性时,可以做岭回归,一般地逐步回归可以直接避免多重复共线性。
二、对于分类任务
(一)对数几率回归(又:Logistic 回归)
1.本质: 是通过对数几率函数: y = 1 / ( 1+ exp(-z) ) 将输出标记 y 限制在(0,1)区间中 。 将z = w’x+b 带入,得到的y 可以看作是样本x 作为正例的概率 ,则 1-y 即反例的概率。
2.优点: 无需假定数据分布 ; 可以得到预测的发生比(Odds) 。
3.参数估计方法: 极大似然法,或从信息论角度出发,使得相对熵最小化(等价于使得交叉熵最小化)。 这是理论推导,在具体求参数时,可以使用梯度下降法或牛顿法求解。
(二)线性判别分析(LDA)
1.**思想:**以二分类问题为例。对于给定的训练数据集,将样例投影到一条直线上:y = w’x ,使得正例的投影点之间尽可能近,反例的投影点之间尽可能近;正反例的投影点之间尽可能远。 (注:就是在已知了研究对象为若干组的分类情况下,判别新的观测样本属于哪一类,是一种有监督的学习方法)。
2.**目标:**最大化类间散度矩阵与类内散度矩阵的广义瑞利商。
3.**参数估计方法:**利用Lagrange乘子法 可转换得 w .
注1:由于正例与负例是根据输出值 y 分成的两个组,我们也可以通过度量新样本到两个组的平方马氏距离远近来对新样本进行分类 ,涉及《多元统计分析》中判别分析知识(线性判别分析相当于是其中一种类型,还有如贝叶斯判别,Fisher 判别)。
注2:也可以处理多分类情形 。
(三)多分类学习
1.思想:将多分类任务拆分若干个二分类任务求解,为每一个二分类任务训练一个分类器,再对分类器的结果进行集成,作为多分类任务的结果。
2.拆分策略:
比如N 个类别的多分类问题:
(1)一对一(OvO):N个类别两两配对,拆分为了二分类任务,就可以利用上述对数几率回归、线性判别分析等方法训练得到N(N-1)/2 个分类器,对于新样本,将预测类别最多的类作为新样本的类。
(2)一对其余(OvR)
(3)多对多(MvM):利用“纠错输出码”思想。
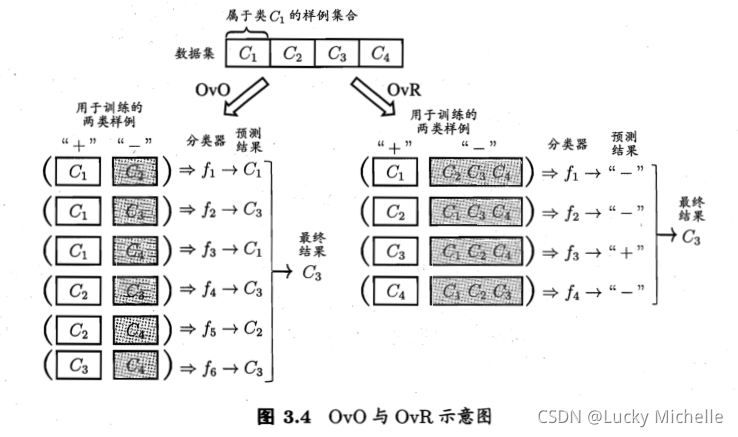
注:对于类别不平衡情形,即不同类别的训练样本数差距大,常见方法为:欠采样、过采样、“再缩放”。
参考书:《机器学习》周志华老师