（一）绘制图像
1、绘制图像用命令plot(x,y)；
但如果想在一幅图上绘制两条曲线，那么绘制完后补充命令hold on;再绘制另一条曲线，还可以用’r’标注这条曲线为红色；
用xlabel标签标注横轴，用ylabel标签标注纵轴；legend命令在右上角标注两种曲线分别代表什么；
用title标注图表标题。
这样绘制出来的图像是这样的：
如果你想把这张图片保存到桌面，可以输入命令：
2、如果你想关闭当前作图，输入close即可；
如果你想使这两个图分开绘制，可以分别给它们命名figure1、figure2绘制。
>>close
>>figure(1):plot(t,y1);
>>figure(2):plot(t,y2);
使用subplot(1,2,1)命令展开图像使之分为12格，现在用第1格作图；
使用subplot(1,2,2)命令展开图像使之分为12格，现在用第2格作图。
3、如果需要调整绘图刻度，使用axis命令。
%调整图的横轴为0.5到1，纵轴为-1到1
>>axis([0.5 1 -1 1])
这里后绘制图2，所以只对图2起作用：
4、使用clf;命令清除画布；
使用imagesc(A)命令将矩阵绘制在画布上，不同的数字对应不同的颜色；
imagesc(A),colorbar,colormap gray;三条命令同时执行，意味着在图右方再绘制一个色彩条，用不同深浅的灰色表示数值大小。
绘制效果：
5、在同一行中：用,分隔的命令可以同时执行，用;分隔的命令可以同时执行而且不输出。
（二）Octave程序中写控制语句
1、for循环：
2、while循环：让v向量中前5个数置为100。（空格不空格不影响结果）
如果再在里面嵌套一个if语句，格式如下：
3、if结构
另外，输入exit或者quit命令是退出Octave软件。
（三）Octave调用其他文件中的函数
1、我在本地桌面上预先定义文件名为squarethisnumber.m的文件，文件内容是一个定义好的函数：（Octave可以同时返回多个值，这非常少见）
function [y1,y2] = squareThisNumber(x)
y1 = x^2;
y2 = x^3;
那么我们如何调用？
>>cd 'C:\Users\chen\Desktop'
>>[a,b] = squareThisNumber(5);
>>a
>>b
即可得到a = 25，b = 125。
2、假设我现在有训练样本集（1,1）（2,2）（3,3），现在我要找到不同C塔值对应的代价函数值J，应该怎么做？
首先，在桌面文件上写下代价函数J的定义：
在Octave中输入矩阵，并定义C塔：
它计算出j=0。那是因为我们C塔0=0，C塔1=1（即theta=[0:1]），这与我们的预期是符合的。
如果设置theta=[0:0]，计算出来的j=2.3333，也就是:
(1^2 + 2^2 + 3^2)/(2*3) = 2.3333
j值不是最小的了。
（四）矢量
1、在使用线性回归时，如果有十个以上的特征（变量数），建议向量化。这可以减少代码实现相同的功能。
例如：下面这个假设函数用两种方法表示，左边这种是将C塔、xj看作两个数字，应用for循环实现遍历（因为在matlab中下标从1开始，C塔0只能用C塔1表示，所以这里是1到n+1）；右边是分别将这些数表示成两个向量时，只要一行代码便能轻松实现。
再举一个例子：线性回归中梯度下降的更新方程。
我们首先展开前面三项，注意：这些式子要实现同步更新，不能异步算值，会影响其他参数。
我们可以分别将左边的C塔0、C塔1、C塔2…组成一个向量C塔（n+1维），右边的阿法是一个实数，剩下的部分也可以组成一个向量。
因为将其展开可以看出相当于一个实数乘以x1、一个实数乘以x2…相当于X向量中的数字变大或变小了，但整体还是可以组成一个向量。
（五）分类
1、当预测的变量是一个离散值时一般认为其是一个分类问题。
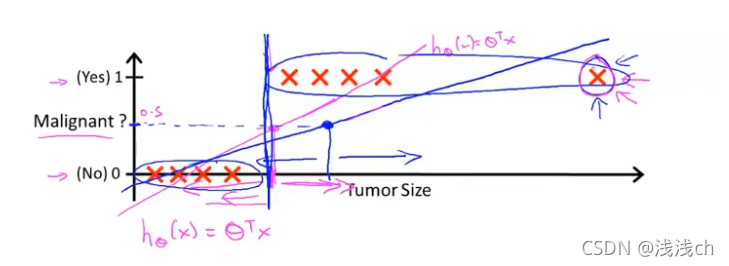
继续使用线性回归的方法处理分类问题，往往得到的预测结果并不准确（以上次讲的判断乳腺癌肿瘤是良性还是恶性的分类问题为例）：
分类问题也称为Logistic回归问题，一般假设函数的输出值会在[0,1]范围内，标签值y一般是0或1。
2、分类问题的假设陈述
分类问题的假设函数hc塔(x)如下，被称为Sigmoid function或Logistic function函数，函数图像如下：
现在需要用参数C塔来拟合我们的数据，那么hc塔(x)的值描述的是：
在给定x（输入x）的条件下y=1的概率。
