深度学习
随机梯度下降(SDG)与批量梯度下降(BDG)
| 方法 | 特点 |
|---|---|
| BDG | 1.采用所有数据进行梯度下降操作 2.在样本较多即数据量较大时训练速度很慢 |
| SDG | 1.SDG使用一个样本进行梯度下降操作; 2.训练速度很快; 3.由于采用一个样本运算,因此有可能得到的不是全局最优解; 4.由于使用一个样本操作导致迭代的方向变化很大,因此不能很快的收敛到局部最优解 |
Bootstrapping
??一种再抽样的统计方法。将“自助统计量”与“观察统计量”的关系≈“观察统计量”与“真值”的关系。
??再抽样的定义:
??①假定观察值便是总体
??②由这一假定的总体抽取样本,即再抽样。
Attention机制
(明天再写,先看几篇论文)
机器学习
交叉熵
(1)信息量
??x为离散型随机变量,其概率分布为p(x),则有信息量定义:
I
(
x
0
)
=
?
l
o
g
(
p
(
x
0
)
)
I(x_0)=-log(p(x_0))
I(x0?)=?log(p(x0?))
(2)熵
??信息量的期望:
H
(
x
)
=
?
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
p
(
x
i
)
)
H(x)=-\sum_{i=1}^{n}p(x_i)log(p(x_i))
H(x)=?i=1∑n?p(xi?)log(p(xi?))
(3)相对熵(KL散度)
??同一个随机变量x,有两个单独的概率分布p、q(如真实值分布与样本值分布),相对熵描述两者等价时所需的信息增量。
D
K
L
(
P
∣
∣
Q
)
=
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
p
(
x
i
)
q
(
x
i
)
)
D_{KL} (P||Q)=\sum_{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)} )
DKL?(P∣∣Q)=i=1∑n?p(xi?)log(q(xi?)p(xi?)?)
(4)交叉熵
D
K
L
(
P
∣
∣
Q
)
=
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
p
(
x
i
)
q
(
x
i
)
)
D_{KL} (P||Q)=\sum_{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)} )
DKL?(P∣∣Q)=i=1∑n?p(xi?)log(q(xi?)p(xi?)?)
=
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
p
(
x
i
)
?
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
q
(
x
i
)
)
=\sum_{i=1}^{n}p(x_i)log(p(x_i)-\sum_{i=1}^{n}p(x_i)log(q(x_i))
=i=1∑n?p(xi?)log(p(xi?)?i=1∑n?p(xi?)log(q(xi?))
=
?
H
(
x
)
+
[
?
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
q
(
x
i
)
)
]
=-H(x)+[-\sum_{i=1}^{n}p(x_i)log(q(x_i))]
=?H(x)+[?i=1∑n?p(xi?)log(q(xi?))]
??其中,前者-H(x)为p的熵,一般为已知常量;后者为交叉熵,记为:
H
(
p
,
q
)
=
?
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
q
(
x
i
)
)
H(p,q)=-\sum_{i=1}^{n}p(x_i)log(q(x_i))
H(p,q)=?i=1∑n?p(xi?)log(q(xi?))
??在机器学习中,通常使用KL散度评估label和predict之间的距离,而-H(y)一般不变,因此,采用交叉熵可以作为loss函数评估模型。故其物理意义是预测输出与期望输出间的度量。
Multi-task Learning
单任务学习与多任务学习的区别
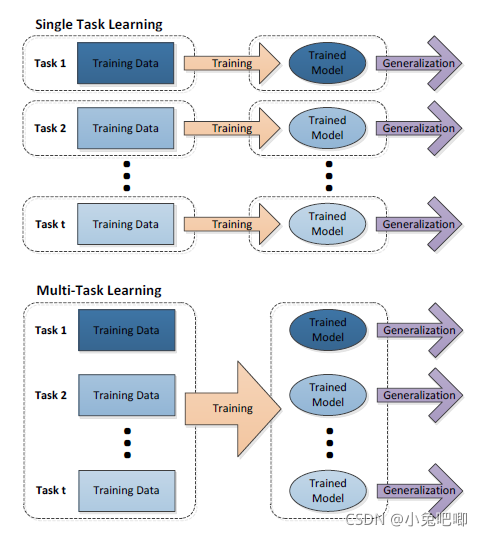
多任务学习的定义:
??基于共享表示,把多个相关的任务放在一起学习的一种机器学习方法。
强化学习
SumTree
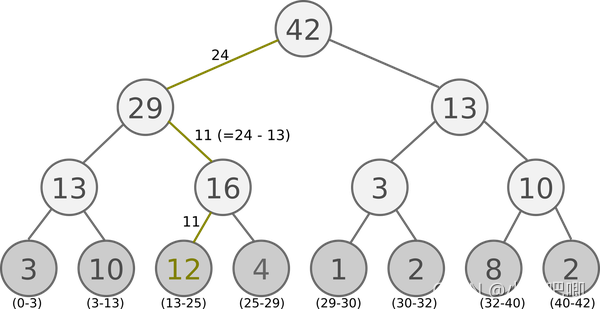
??Sum-Tree类比Binary heap,但每个父节点的优先值是其子节点优先值的和。应用于DQN with Prioritized Experience Reply的优先级取样中。抽样步骤如下:
??①按batch_size分割区间:
n
=
s
u
m
(
p
)
b
a
t
c
h
s
i
z
e
n=\frac{sum(p)}{batchsize}
n=batchsizesum(p)?
??②每个区间中随机选取一个数值,如下图中在[13,25)区间中选择24。
??③按照下列公式向下搜索不断向下搜索,直到找到最后的priority和对应的数据。