目录
一、单目初始化中的特征匹配SearchForInitialization
如何制作、生成BoW? 为什么 BOW一般用 BRIEF描述子?
一、单目初始化中的特征匹配SearchForInitialization
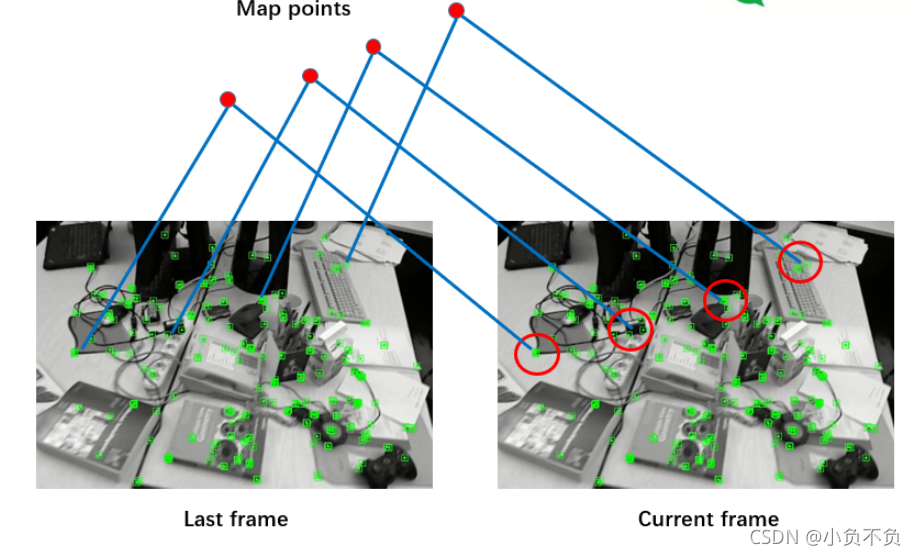
?计算描述子的距离(汉明距离)距离最短则为匹配点
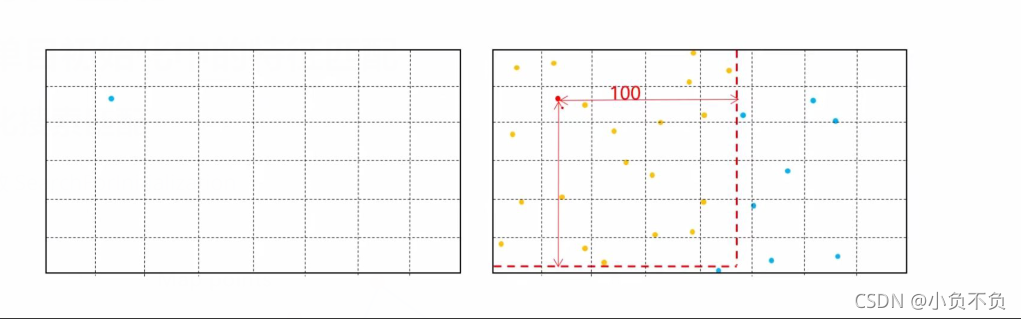
?1、匹配点要大于100才能进行初始化
如上图所示,找出第二张图片中对应第一张图片的特征点,并在特征点周围以100为半径,做一个框框,在这个范围里面找符合要求的特征点。
快速匹配和候选特征点GetFeaturesInArea
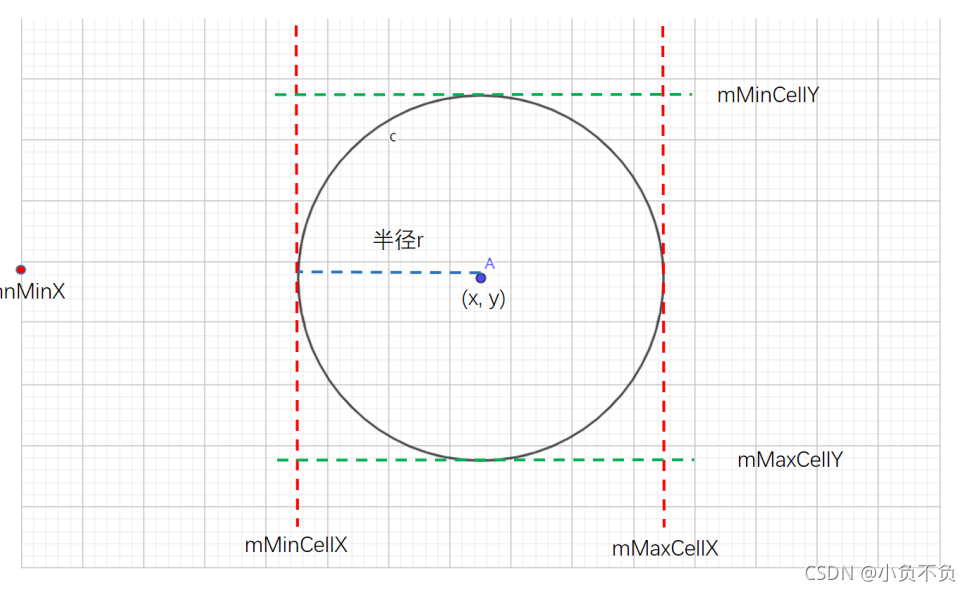
?2、挑选出来的特征点所属金字塔必须为第0层
3、剔除那些在所选格子内但是不在搜索范围内的点
4、最优距离要小于50,计算最优距离和最次距离的比值
5、统计匹配点方向的直方图
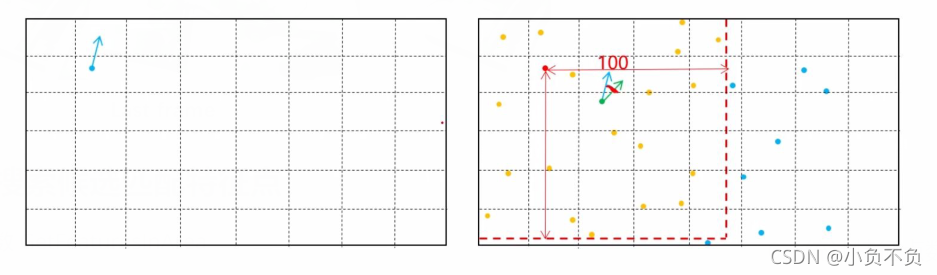
? ? ? ? 计算第一张图片FAST特征点方向和第二张图片FAST特征点方向,并将第一张特征点的方向向量移动到第二张图片上面,计算两个方向向量的角度,做一个直方图。
6、统计特征点数量最多的三个方向
7、判断第二多的数量<0.1第一多的数量。符合则证明第一多为主方向
8、判断第三多的数量<0.1第一多的数量。符合则证明第一多和第二多的主方向
二、跟踪(TrackwithModel)
根据匀速模型来计算初始位姿,然后通过投影的形式搜索匹配点
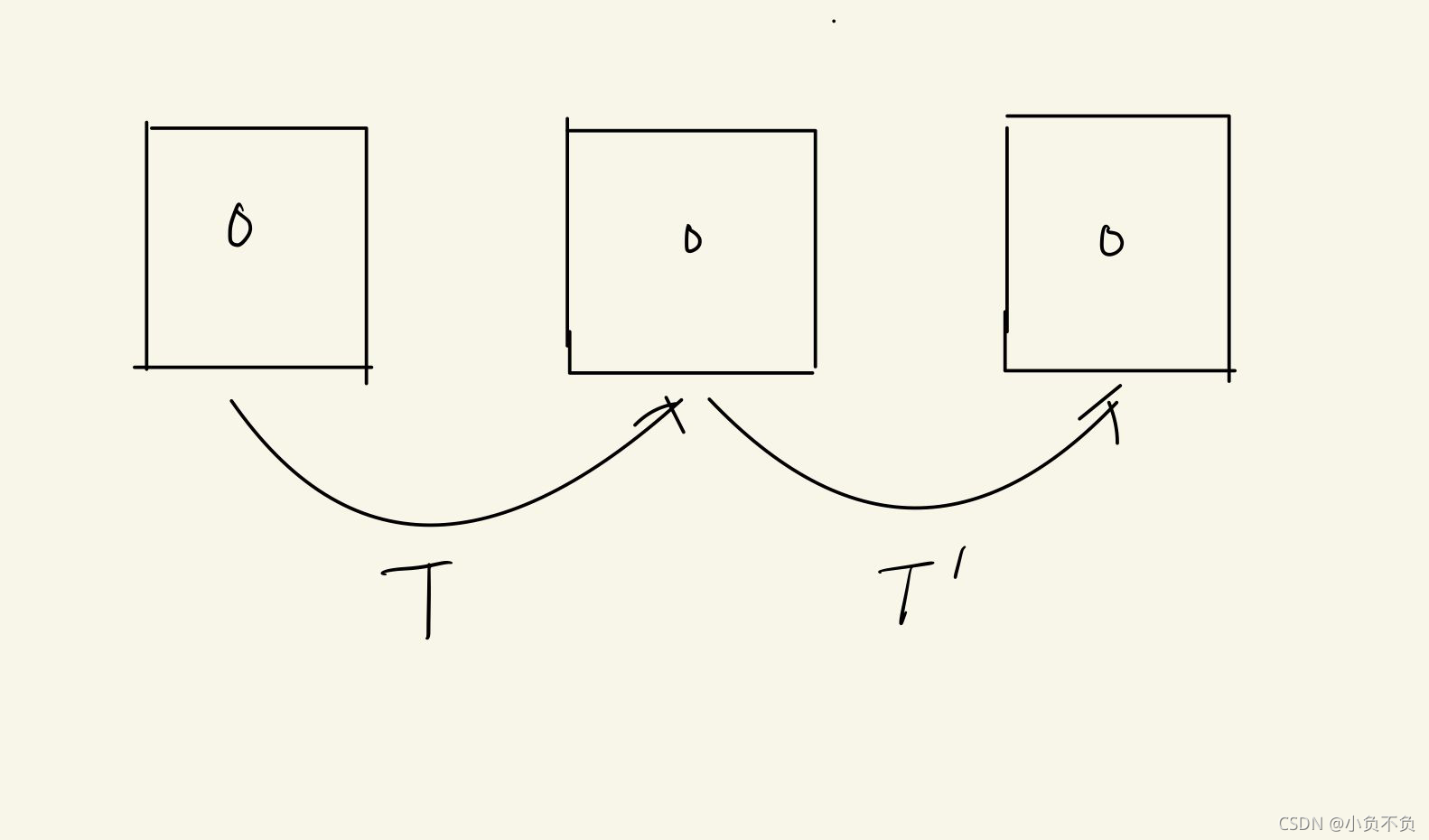
?TrackReferenceKeyFrame
1、前面EPnP得到的内容将不再进行跟踪搜索
2、这里需要估计关键帧地图点在当前在帧图像金字塔的层数
图像金字塔的层数怎么的来:通过地图点离相机光心的距离计算而来
3、和前面的seachByProjection类似,将关键帧地图点投影到当前帧,然后在一定范围内搜索
三、词袋介绍BoW
1、直观理解词袋
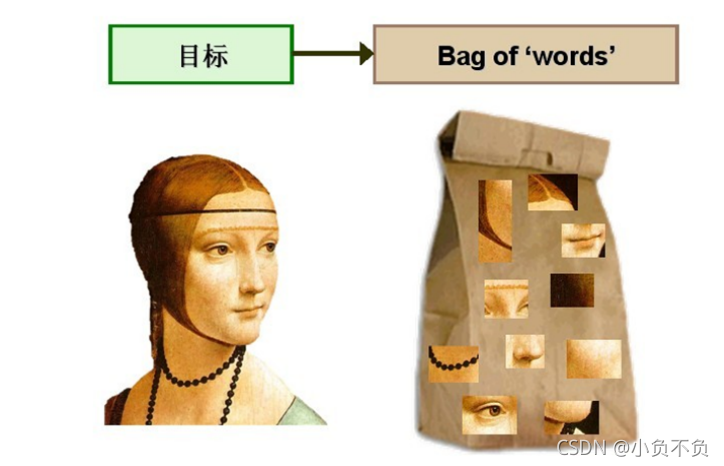
?如何找到匹配的图像
特征匹配
不同的光照强度都会有影响,而且匹配时间较长
词袋模型(BoW)
2、词袋基本思想
从单词概念引入基本思想
如何定量描述
s---评分计算函数
a&b----二进制向量
W---向量维度
1---向量L1范数,各元素绝对值之和
由此定义了描述向量的相似性,即图像的相似程度
3、从字典结构到k-d树
k:每层的节点数为k
d:数结构一共有d 层
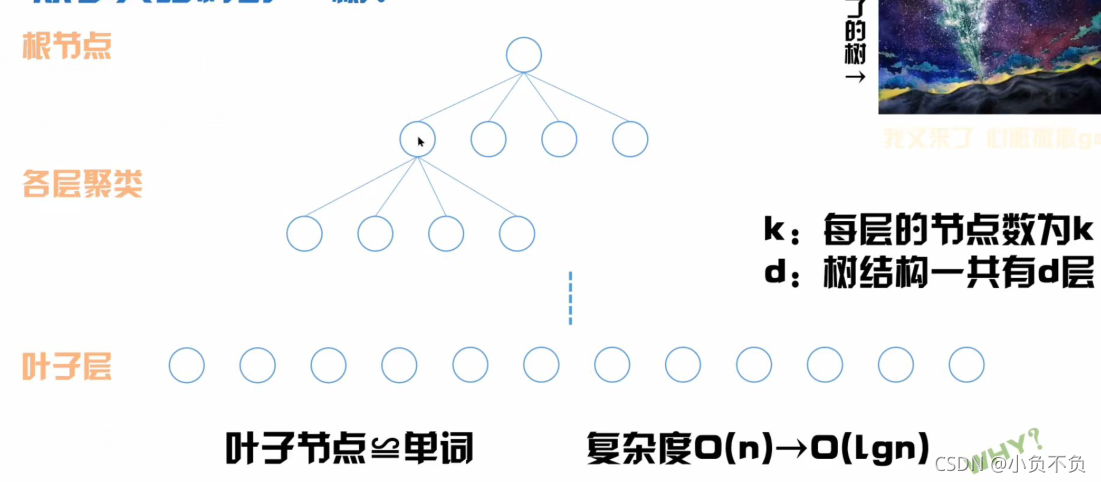
单词:局部相邻特征点的集合
功能:把图片中所有的行人归到人这个类中
字典:具有一定结构的单词索引,从大量图片训练而来
那么有了一个特征点,如何找到匹配的单词
从字典结构到K-d树(两种索引方式)

K-means聚类
 ?
?
1、首先随机生成K个聚类中心点
2、根据聚类中心点,将数据分为K类。分类原则是数据离哪个中心点近就将它分为哪一类
3、再根据分好的类别数据,重新计算聚类的类别中心点
4、不断的重复2和3步,直到中心点不再变化
注:刚开始生成的中心点不同对后面也会有不同的影响
4、相似度计算TF-IDF
TF:某单词在一副图像中出现的频率越高,该单词就更具代表性
IDF:某单词在字典中出现的频率越低,就说明该单词在字典中更具有代表性
图片维度
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???
字典维度
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
?权重
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???
相似度计算 BoW向量(bog of words)
BoW向量组成如下,两元素分别为单词和权重
该向量描述了一张图像,包含图像中有哪些单词,以及对应的权重是多少,进而,通过人为规定范数的形式,就能够计算出两张图片的相似程度
5、总结词袋模型
step1、从大量的图片中提取特征采用聚类法生成单词构建字典
step2、处理某一帧图片,采用TF-IDF计算单词权重
step3、生成该帧的BoW向量,更新正向索引和倒排索引的内容
生成BoW向量就是图片的新名片,可以用来回环检测、匹配图像、优化位姿、寻找特征点等
四、词袋大概流程
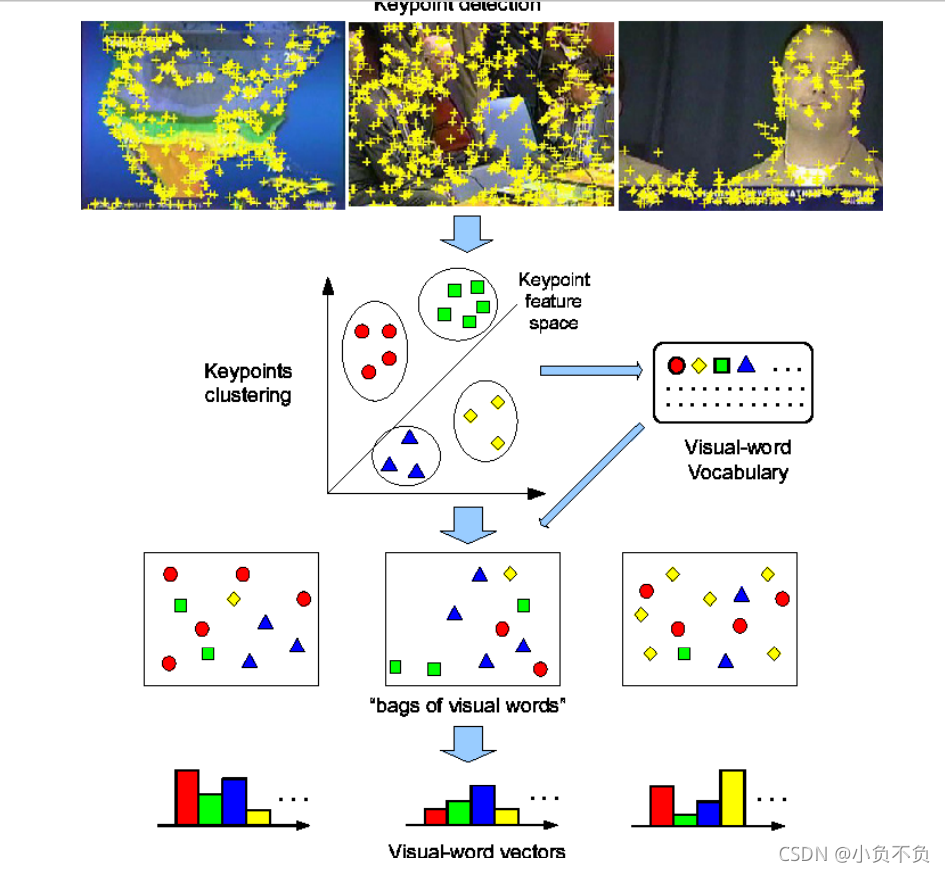
为什么叫 bag of words 而不是 list of words 或者 array of words?
因为丢弃了Word出现的排列顺序、位置等因素,只考虑出现的频率,大大简化了表达,节省了存储空 间,在分析对比相似度的时候非常高效
闭环检测:
核心就是判断两张图片是否是同一个场景,也就是判断图像的相似性。
?如何计算两张图片的相似性
Bag of words 可以解决这个问题。是以图像特征集合作为visual words,只关心图像中有没有这些 words,有多少次,更符合人类认知方式,对不同光照、视角变换、季节更替等非常鲁棒。
加速匹配
ORB-SLAM2代码中使用的 SearchByBoW(用于关键帧跟踪、重定位、闭环检测SIM3计算),以及局部 地图里的SearchForTriangulation,内部实现主要是利用了 BoW中的FeatureVector 来加速特征匹配。
使用FeatureVector 避免了所有特征点的两两匹配,只比较同一个节点下的特征点,极大加速了匹配效 率,至于匹配精度,论文 《Bags of Binary Words for Fast Place Recognition in Image Sequences 》 中提到在26292 张图片里的 false positive 为0,说明精度是有保证的。实际应用中效果非常不错。
缺点
需要提前加载离线训练好的词袋字典,增加了存储空间。但是带来的优势远大于劣势,而且也有不少改 进方法比如用二进制存储等来压缩词袋,减少存储空间,提升加载速度。
如何制作、生成BoW? 为什么 BOW一般用 BRIEF描述子?
速度方面
因为计算和匹配都非常快,论文中说大概一个关键点计算256位的描述子只需要 17.3μs 因为都是二进制描述子,距离描述通过汉明距离,使用异或操作即可,速度非常快。 而SIFT, SURF 描述子都是浮点型,需要计算欧式距离,会慢很多。
在Intel Core i7 ,2.67GHz CPU上,使用FAST+BRIEF 特征,在26300帧图像中 特征提取+词袋位置识别 耗时 22ms 每帧。
在精度方面
先上结论:闭环效果并不比SIFT, SURF之类的高精度特征点差。
具体来看一下对比: 以下对比来自论文《2012,Bags of Binary Words for Fast Place Recognition in Image Sequences, IEEE TRANSACTIONS ON ROBOTICS》
三种描述子 BRIEF,,SURF64 ,U-SURF128 使用同样的参数,在训练数据集NewCollege,Bicocca25b 上的 Precision-recall 曲线
其中SURF64:带旋转不变性的 64 维描述子
U-SURF128:不带旋转不变性的128维描述子
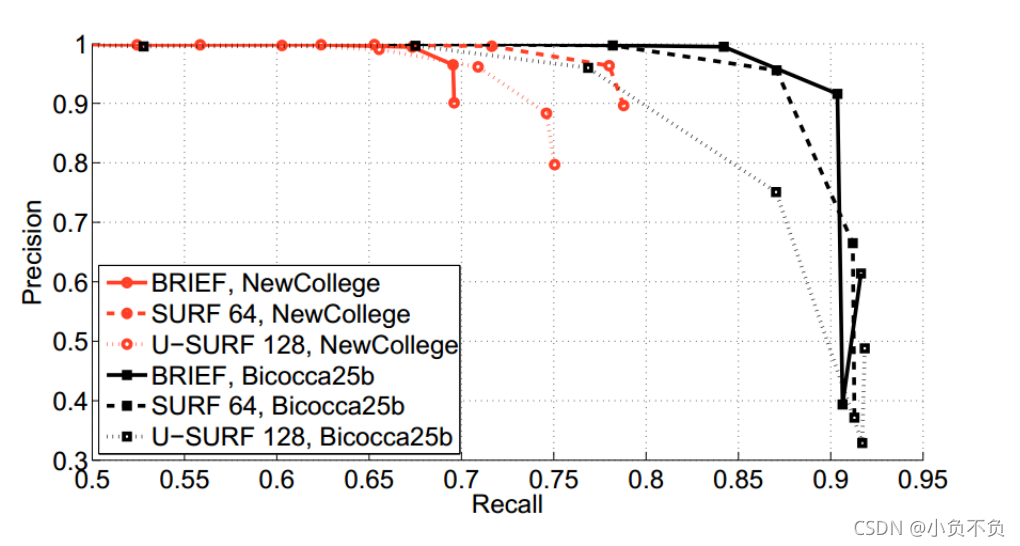
在两个数据中,SURF64 都明显比 U-SURF128 表现的好(曲线下面积更大),可以看到在Bicocca25b 数据集上,BRIEF明显比 U-SURF128 好,比SURF64 也稍微好一些,在NewCollege 数据集上 SURF64 比 BRIEF 更好一点,但是BRIEF也仍然不错。
总之,BRIEF 和 SURF64 效果基本相差不大,可以说打个平手。?
可视化效果
可视化看一下效果
下图左边图片对是BRIEF 在vocabulary 中同样的Word下的回环匹配结果,同样的特征连成了一条线。
下图右边图像对是同样数据集中SURF64 的闭环匹配结果。
第一行 来看,尽管有一定视角变换,BRIEF 和 SURF64 的匹配结果接近
第二行:BRIEF成功进行了闭环,但是SURF64 没有闭环。原因是SURF64 没有得到足够多的匹配关系。
第三行:BRIEF 闭环失败而SURF64闭环成功。
我们分析一下原因:主要和近景远景有关。因为BRIEF相比SURF64没有尺度不变性,所以在尺度变换较 大的近景很容易匹配失败,比如第三行。而在中景和远景,由于尺度变化不大,BRIEF 表现接近甚至优 于SURF64

?不过,我们通过图像金字塔可以解决上述BRIEF的尺度问题。论文中作者也提到了ORB + BRIEF的特征点 主要问题是没有旋转不变性和尺度不变性。不过目前都解决了。
总之,BRIEF的闭环效果值得信赖!
离线训练 vocabulary tree(也称为字典)
首先图像提取ORB 特征点,将描述子通过 k-means 进行聚类,根据设定的树的分支数和深度,从叶子 节点开始聚类一直到根节点,最后得到一个非常大的 vocabulary tree,
1、遍历所有的训练图像,对每幅图像提取ORB特征点。
2、设定vocabulary tree的分支数K和深度L。将特征点的每个描述子用 K-means聚类,变成 K个集合, 作为vocabulary tree 的第1层级,然后对每个集合重复该聚类操作,就得到了vocabulary tree的第2层 级,继续迭代最后得到满足条件的vocabulary tree,它的规模通常比较大,比如ORB-SLAM2使用的离 线字典就有108万+ 个节点。
3、离根节点最远的一层节点称为叶子或者单词 Word。根据每个Word 在训练集中的相关程度给定一个 权重weight,训练集里出现的次数越多,说明辨别力越差,给与的权重越低。
在线图像生成BoW向量
1、对新来的一帧图像进行ORB特征提取,得到一定数量(一般几百个)的特征点,描述子维度和 vocabulary tree中的一致
2、对于每个特征点的描述子,从离线创建好的vocabulary tree中开始找自己的位置,从根节点开始, 用该描述子和每个节点的描述子计算汉明距离,选择汉明距离最小的作为自己所在的节点,一直遍历到 叶子节点。
整个过程是这样的,见下图。紫色的线表示 一个特征点从根节点到叶子节点的过程。
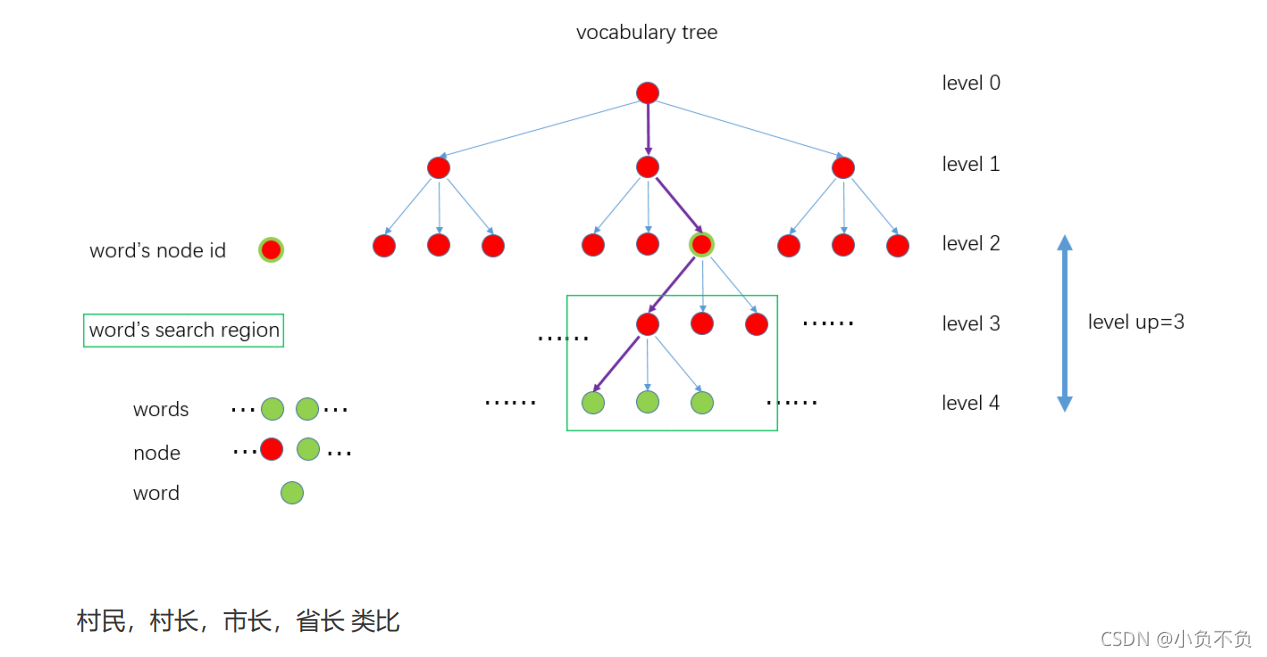
源码解析?
一个描述子转化为Word id, Word weight,节点所属的父节点(距离叶子深度为level up深度的节点) id 对应的实现代码见:
/**
* @brief 将描述子转化为Word id, Word weight,节点所属的父节点id(这里的父节点不是叶子的上
一层,它距离叶子深度为levelsup)
* @tparam TDescriptor
* @tparam F
* @param[in] feature 特征描述子
* @param[in & out] word_id Word id
* @param[in & out] weight Word 权重
* @param[in & out] nid 记录当前描述子转化为Word后所属的 node id,它距离
叶子深度为levelsup
* @param[in] levelsup 距离叶子的深度
*/
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor,F>::transform(const TDescriptor &feature,
WordId &word_id, WordValue &weight, NodeId *nid, int levelsup) const
{
// propagate the feature down the tree
vector<NodeId> nodes;
typename vector<NodeId>::const_iterator nit;
// level at which the node must be stored in nid, if given
// m_L: depth levels, m_L = 6 in ORB-SLAM2
// nid_level 当前特征点转化为的Word 所属的 node id,方便索引
const int nid_level = m_L - levelsup;
if(nid_level <= 0 && nid != NULL) *nid = 0; // root
NodeId final_id = 0; // root
int current_level = 0;
do
{
++current_level;
nodes = m_nodes[final_id].children;
final_id = nodes[0];
// 取当前节点第一个子节点的描述子距离初始化最佳(小)距离
double best_d = F::distance(feature, m_nodes[final_id].descriptor);
// 遍历nodes中所有的描述子,找到最小距离对应的描述子
for(nit = nodes.begin() + 1; nit != nodes.end(); ++nit)
{
NodeId id = *nit;
double d = F::distance(feature, m_nodes[id].descriptor);
if(d < best_d)
{
best_d = d;
final_id = id;
}
}
// 记录当前描述子转化为Word后所属的 node id,它距离叶子深度为levelsup
if(nid != NULL && current_level == nid_level)
*nid = final_id;
} while( !m_nodes[final_id].isLeaf() );
// turn node id into word id
// 取出 vocabulary tree中node距离当前feature 描述子距离最小的那个node的 Word id 和
weight
word_id = m_nodes[final_id].word_id;
weight = m_nodes[final_id].weight;
}
一幅图像里所有特征点转化为两个std::map容器 BowVector 和 FeatureVector 的代码见:
/**
* @brief 将一幅图像所有的特征点转化为BowVector和FeatureVector
*
* @tparam TDescriptor
* @tparam F
* @param[in] features 图像中所有的特征点
* @param[in & out] v BowVector
* @param[in & out] fv FeatureVector
* @param[in] levelsup 距离叶子的深度
*/
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor,F>::transform(
const std::vector<TDescriptor>& features,
BowVector &v, FeatureVector &fv, int levelsup) const
{
v.clear();
fv.clear();
if(empty()) // safe for subclasses
{
return;
}
// normalize
// 根据选择的评分类型来确定是否需要将BowVector 归一化
LNorm norm;
bool must = m_scoring_object->mustNormalize(norm);
typename vector<TDescriptor>::const_iterator fit;
if(m_weighting == TF || m_weighting == TF_IDF)
{
unsigned int i_feature = 0;
// 遍历图像中所有的特征点
for(fit = features.begin(); fit < features.end(); ++fit, ++i_feature)
{
WordId id; // 叶子节点的Word id
NodeId nid; // FeatureVector 里的NodeId,用于加速搜索
WordValue w; // 叶子节点Word对应的权重
// 将当前描述子转化为Word id, Word weight,节点所属的父节点id(这里的父节点不是叶的上一层,它距离叶子深度为levelsup)
// w is the idf value if TF_IDF, 1 if TF
transform(*fit, id, w, &nid, levelsup);
if(w > 0) // not stopped
{
// 如果Word 权重大于0,将其添加到BowVector 和 FeatureVector
v.addWeight(id, w);
fv.addFeature(nid, i_feature);
}
}
if(!v.empty() && !must)
{
// unnecessary when normalizing
const double nd = v.size();
for(BowVector::iterator vit = v.begin(); vit != v.end(); vit++)
vit->second /= nd;
}
}
// 省略掉了IDF || BINARY情况的代码
if(must) v.normalize(norm);
}
相当于将当前图像信息进行了压缩,并且对后面特征点快速匹配、闭环检测、重定位意义重大。 这两个容器非常重要,下面一个个来解释:
理解词袋向量BowVector
它内部实际存储的是这个
std::map<WordId,Woedvalue>
其中 WordId 和 WordValue 表示Word在所有叶子中距离最近的叶子的id 和权重(后面解释)。 同一个Word id 的权重是累加更新的,见代码
void BowVector::addWeight(WordId id, WordValue v)
{
// 返回指向大于等于id的第一个值的位置
BowVector::iterator vit = this->lower_bound(id);
// http://www.cplusplus.com/reference/map/map/key_comp/
if(vit != this->end() && !(this->key_comp()(id, vit->first)))
{
// 如果id = vit->first, 说明是同一个Word,权重更新
vit->second += v;
}
else
{
// 如果该Word id不在BowVector中,新添加进来
this->insert(vit, BowVector::value_type(id, v));
}
}
理解特征向量FeatureVector
内部实际是个
std::map <Nodeid,std:;vector<unsigned int>>
其中NodeId 并不是该叶子节点直接的父节点id,而是距离叶子节点深度为level up对应的node 的id, 对应上面 vocabulary tree 图示里的 Word's node id。为什么不直接设置为父节点?因为后面搜索该 Word 的匹配点的时候是在和它具有同样node id下面所有子节点中的Word 进行匹配,搜索区域见图示 中的 Word's search region。所以搜索范围大小是根据level up来确定的,level up 值越大,搜索范围越广,速度越慢;level up 值越小,搜索范围越小,速度越快,但能够匹配的特征就越少。 另外 std::vector 中实际存的是NodeId 下所有特征点在图像中的索引。见代码
void FeatureVector::addFeature(NodeId id, unsigned int i_feature)
{
FeatureVector::iterator vit = this->lower_bound(id);
// 将同样node id下的特征放在一个vector里
if(vit != this->end() && vit->first == id)
{
vit->second.push_back(i_feature);
}
else
{
vit = this->insert(vit, FeatureVector::value_type(id,
std::vector<unsigned int>() ));
vit->second.push_back(i_feature);
}
}
FeatureVector主要用于不同图像特征点快速匹配,加速几何关系验证,比如 ORBmatcher::SearchByBoW 中是这样用的
DBoW2::FeatureVector::const_iterator f1it = vFeatVec1.begin();
DBoW2::FeatureVector::const_iterator f2it = vFeatVec2.begin();
DBoW2::FeatureVector::const_iterator f1end = vFeatVec1.end();
DBoW2::FeatureVector::const_iterator f2end = vFeatVec2.end();
while(f1it != f1end && f2it != f2end)
{
// Step 1:分别取出属于同一node的ORB特征点(只有属于同一node,才有可能是匹配点)
if(f1it->first == f2it->first)
// Step 2:遍历KF中属于该node的特征点
for(size_t i1=0, iend1=f1it->second.size(); i1<iend1; i1++)
{
const size_t idx1 = f1it->second[i1];
MapPoint* pMP1 = vpMapPoints1[idx1];
// 省略
// ..........
词典树的保存和加载
我们将 vocabulary tree翻译为词典树
如何保存训练好的词典树存储为txt文件?
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor,F>::saveToTextFile(const std::string
&filename) const
{
fstream f;
f.open(filename.c_str(),ios_base::out);
// 第一行打印 树的分支数、深度、评分方式、权重计算方式
f << m_k << " " << m_L << " " << " " << m_scoring << " " << m_weighting <<
endl;
for(size_t i=1; i<m_nodes.size();i++)
{
const Node& node = m_nodes[i];
// 每行第1个数字为父节点id
f << node.parent << " ";
// 每行第2个数字标记是(1)否(0)为叶子(Word)
if(node.isLeaf())
f << 1 << " ";
else
f << 0 << " ";
// 接下来存储256位描述子,最后存储节点权重
f << F::toString(node.descriptor) << " " << (double)node.weight << endl;
}
f.close();
}
如何加载训练好的词典树文件?
/**
* @brief 加载训练好的 vocabulary tree,txt格式
*
* @tparam TDescriptor
* @tparam F
* @param[in] filename vocabulary tree 文件名称
* @return true 加载成功
* @return false 加载失败
*/
template<class TDescriptor, class F>
bool TemplatedVocabulary<TDescriptor,F>::loadFromTextFile(const std::string
&filename)
{
ifstream f;
f.open(filename.c_str());
if(f.eof())
return false;
m_words.clear();
m_nodes.clear();
string s;
getline(f,s);
stringstream ss;
ss << s;
ss >> m_k; // 树的分支数目
ss >> m_L; // 树的深度
int n1, n2;
ss >> n1;
ss >> n2;
if(m_k<0 || m_k>20 || m_L<1 || m_L>10 || n1<0 || n1>5 || n2<0 || n2>3)
{
std::cerr << "Vocabulary loading failure: This is not a correct text
file!" << endl;
return false;
}
m_scoring = (ScoringType)n1; // 评分类型
m_weighting = (WeightingType)n2; // 权重类型
createScoringObject();
// 总共节点(nodes)数,是一个等比数列求和
//! bug 没有包含最后叶子节点数,应该改为 ((pow((double)m_k, (double)m_L + 2) -
1)/(m_k - 1))
//! 但是没有影响,因为这里只是reserve,实际存储是一步步resize实现
int expected_nodes =
(int)((pow((double)m_k, (double)m_L + 1) - 1)/(m_k - 1));
m_nodes.reserve(expected_nodes);
// 预分配空间给 单词(叶子)数
m_words.reserve(pow((double)m_k, (double)m_L + 1));
// 第一个节点是根节点,id设为0
m_nodes.resize(1);
m_nodes[0].id = 0;
while(!f.eof())
{
string snode;
getline(f,snode);
stringstream ssnode;
ssnode << snode;
// nid 表示当前节点id,实际是读取顺序,从0开始
int nid = m_nodes.size();
// 节点size 加1
m_nodes.resize(m_nodes.size()+1);
m_nodes[nid].id = nid;
// 读每行的第1个数字,表示父节点id
int pid ;
ssnode >> pid;
// 记录节点id的相互父子关系
m_nodes[nid].parent = pid;
m_nodes[pid].children.push_back(nid);
// 读取第2个数字,表示是否是叶子(Word)
int nIsLeaf;
ssnode >> nIsLeaf;
// 每个特征点描述子是256 bit,一个字节对应8 bit,所以一个特征点需要32个字节存储。
// 这里 F::L=32,也就是读取32个字节,最后以字符串形式存储在ssd
stringstream ssd;
for(int iD=0;iD<F::L;iD++)
{
string sElement;
ssnode >> sElement;
ssd << sElement << " ";
}
// 将ssd存储在该节点的描述子
F::fromString(m_nodes[nid].descriptor, ssd.str())
// 读取最后一个数字:节点的权重(Word才有)
ssnode >> m_nodes[nid].weight;
if(nIsLeaf>0)
{
// 如果是叶子(Word),存储到m_words
int wid = m_words.size();
m_words.resize(wid+1);
//存储Word的id,具有唯一性
m_nodes[nid].word_id = wid;
//构建 vector<Node*> m_words,存储word所在node的指针
m_words[wid] = &m_nodes[nid];
}
else
{
//非叶子节点,直接分配 m_k个分支
m_nodes[nid].children.reserve(m_k);
}
}
return true;
}