[人工智能]Logistic 回归

创作背景

本菜鸡最近想学学 机器学习，这不，刚开始。
如果觉得我这篇文章写的好的话，能不能给我 点个赞 ，评论 一波。如果要点个 关注 的话也不是不可以🤗

回归与分类的区别

• 回归 要预测的结果是 具体的数值，根据训练数据预测某一输入对应的输出数据。输出的结果是 实数。
• 分类 要判断的结果是 类别，根据训练数据预测 分类正确的概率 （属于 [0, 1]），进而输出 判断的类别 。

回归向分类的转变

既然都是 预测，使用相同的 x ，只是输出从原来的 实数 变成了 类别，那我们就用一个函数将结果从 实数集 映射到 [0, 1] 中，然后再转成对应分类不就行了呗。

• 举个栗子：

  • 有两个类别的实例，o 代表正例，x 代表负例
  • 可以找到一个超平面 $w^{T}x+b=0$ 将两类实例分隔开，即 正确分类
  • 其中，$w\in {\mathbb{R}}^n$ 为超平面的 法向量 ，$b\in \mathbb{R}$ 为 偏置
  • 超平面上方的点都满足 $w^{T}x+b>0$
  • 超平面下方的点都满足 $w^{T}x+b<0$
  • 可以根据以下 x 的线性函数值（与 0 的比较结果）判断实例类别：$z=g(x)=w^{T}x+b$
  • 分类函数以 z 为输入，输出预测的类别：$c=H(z)=H(g(x))$

• 以上是 线性分类器 的基本模型。

有个方法可以实现 线性分类器 ，那就是 Logistic 回归。

• Logistic 回归是一种 广义线性 模型，使用 线性判别式函数 对实例进行分类。

而一般实现这种分类方法的函数是 sigmoid 函数。（因为其中最为出名的是 logistic 函数，所以也被称为 logistic 函数）。

饱和函数

先看一下 饱和函数，至于为什么要看这个函数，因为 Sigmoid 函数都需要满足这个函数，具体见下述 sigmoid （也即 logistic） 函数。

• x < 0 时，导数值 ↑，x ≥ 0 时，导数值 ↓ ，即，将导函数为 正态分布 的分布函数称为 饱和函数 。
• 看一下图像。
  

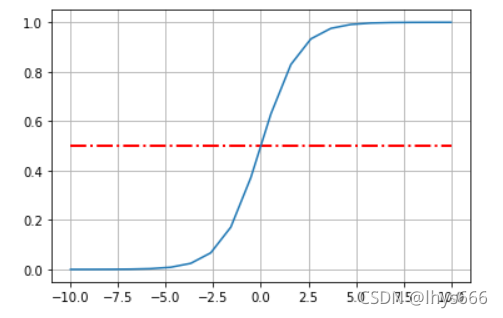
一些饱和函数

• 单位阶跃函数 δ
• $erf(\frac{\sqrt{\pi }}{2}x)$
• $\frac{2}{\pi }\arctan (\frac{\pi }{2}x)$
• $\frac{2}{\pi }gd(\frac{\pi }{2}x)$
• $\frac{x}{1+|x|}$

图像如下

它们的导函数是服从 正态分布 的，图像如下

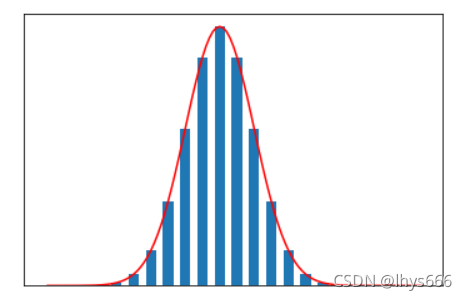
所以，最理想的分类函数为 单位阶跃函数 ，直上直下的，是 饱和函数 的一种。如下图

也就是
$$H(z)=?\begin{array}{l}0,x<0\\ 0.5,x=0\\ 1,x>0\end{array}$$

• 但单位阶跃函数作为分类函数有一个严重缺点，不连续，所以 不是处处可微，使得一些算法不可用（如 梯度下降）。
• 找一个 输入输出特性与单位阶跃函数类似，并且 单调可微的函数 来代替阶跃函数，sigmoid 函数是一种常用替代函数。

sigmoid 函数（logistic 函数）

sigmoid 函数是一类函数，满足以下函数特征即可：

• 有极限
• 单调 增 函数
• 满足 饱和函数 （知道我为什么要提到 饱和函数 了吧(●’?’●)）

函数定义
$$\sigma (x)=\frac{1}{1+e^{?z}}$$

• 一般 $\sigma$ 函数就指 logistic 函数

logistic 函数的值域在 (0,1) 之间连续，函数的输出可视为 x 条件下实例为正例的条件概率 ，即
$$P(y=1|x)=\sigma (g(x))=\frac{1}{1+e^{?(w^{T}x+b)}}$$
x 条件下实例为负例的条件概率为
$$P(y=0|x)=1?\sigma (g(x))=\frac{1}{1+e^{(w^{T}x+b)}}$$

logistic 函数是 对数概率函数 的 反函数，一个事件的概率指该事件发生的概率 p 与该事件不发生的概率 1-p 的比值。

• 对数概率为
  $$\log \frac{p}{1?p}$$
• 对数概率大于 0 表明 正例 的概率大，反之，则 负例 的概率大。

Logistic 回归模型假设一个实例为正例的对数概率是输入 x 的 线性函数，即：
$$\log \frac{p}{1?p}=w^{T}x+b$$
反求 p ，即：
$$p=\sigma (g(x))=\frac{1}{1+e^{?(w^{T}x+b)}}$$
logistic 函数有个很好的数学特性，$\sigma (z)$ 一阶导数形式简单，并且关于其本身的函数：
$$\frac{d\sigma (z)}{dz}=\sigma (z)(1?\sigma (z))$$
Logistic 回归模型假设函数为
$$h_{w,b}(x)=\sigma (g(x))=\frac{1}{1+e^{?(w^{T}x+b)}}$$
将 b 纳入权向量 w ，假设函数更改为
$$h_w(x)=\frac{1}{1+e^{?(w^{T}x)}}$$

极大似然估计

• 根据 $h_w(x)$ 的概率意义，有

$$\begin{gathered} P(y=1|x)=h_w(x) \\ P(y=0|x)=1?h_w(x) \end{gathered}$$

• 由此可得，训练集 D 中的某样本 $(x_i,y_i)$ ，模型将输入实例 $x_i$ 预测为类别 $y_i$ 的概率为

$$P(y=y_i|x_i;w)=h_w(x_i{)}^{y_i}(1?h_w(x_i){)}^{1?y_i}$$

• 训练集 D 各样本独立同分布，定义似然函数 L(w) 描述训练集中 m 个样本同时出现的概率，公式如下：

$$\begin{gathered} L(w)={\Pi }_{i=1}^{m}P(y=y_i|x_i;w) \\ =\prod _{i=1}^m{h}_w(x_i{)}^{y_i}(1?h_w(x_i){)}^{1?y_i} \end{gathered}$$

用 极大似然法 估计参数 w 的核心思想是

• 选择参数 w，使得当前已经观测到的数据（训练集中的 m 个样本）最有可能出现（概率最大），即：

$$\hat{w}={arg}_{w}maxL(w)$$

• 为了 方便求极值点 ，可将找 L(w) 的极值点转化为找其对数似然函数 ln(L(w)) 的最大值点，即：

$$\hat{w}={arg}_{w}maxln(L(w))$$

• 根据定义，对数似然函数为

$$l(w)=ln(L(w))=\sum _{i=1}^m{y}_{i}ln(h_w(x_i))+(1?y_i)ln(1?h_w(x_i))$$

梯度下降更新公式

对于 Logistic 回归模型，可以定义其损失为：

$$J(w)=?\frac{1}{m}l(w)=?\frac{1}{m}\sum _{i=1}^m{y}_{i}ln(h_w(x_i))+(1?y_i)ln(1?h_w(x_i))$$

• 此时，求出损失函数 最小值 与求出对数似然函数 最大值 等价，求损失函数最小值依然可以使用 梯度下降算法 ，最终估计出模型参数 $\hat{w}$

计算 J(w) 对分量 $w_j$ 的偏导数（就对上边的公式 求导）

$$\frac{?}{?w_j}J(w)=?\frac{1}{m}\sum _{i=1}^m{y}_{i}ln{h}_w(x_i)+(1?y_i)ln(1?h_w(x_i))$$
$$=?\frac{1}{m}\sum _{i=1}^m{y}_i\frac{?}{?w_j}ln{h}_w(x_i)+(1?y_i)\frac{?}{?w_j}ln(1?h_w(x_i))$$
$$=?\frac{1}{m}\sum _{i=1}^m{y}_i\frac{1}{h_w(x_i)}\frac{?h_w(x_i)}{?z_i}\frac{?z_i}{w_j}+(1?y_i)\frac{1}{1?h_w(x_i)}(?\frac{?h_w(x_i)}{?z_i})\frac{?z_i}{w_j}$$
$$=?\frac{1}{m}\sum _{i=1}^m(y_i\frac{h_w(x_i)?(1?h_w(x_i)}{h_w(x_i)}?(1?y_i)\frac{h_w(x_i)?(1?h_w(x_i))}{(1?h_w(x_i))})\frac{?z_i}{w_j}$$
$$=?\frac{1}{m}\sum _{i=1}^m(y_i?h_w(x_i))\frac{?z_i}{w_j}$$
$$=\frac{1}{m}\sum _{i=1}^m(h_w(x_i)?y_i)x_{ij}$$

• 其中，$h_w(x_i)?y_i$ 可解释为模型预测 $x_i$ 为正例的概率与其实际类别之间的 误差 。

由此可推出梯度 $?J(w)$ 计算公式为
$$?J(w)=\frac{1}{m}\sum _{i=1}^m(h_w(x_i)?y_i)x_i$$

对于随机梯度下降，即 m = 1 时，相应梯度计算公式为
$$?J(w)=(h_w(x_i)?y_i)x_i$$
设学习率为 $\eta$ ，模型参数 w 的更新公式为
$$w=w?\eta ?J(w)$$

代码实现

自己实现

既然我们已经了解了 Logistic 模型的数学原理，那现在我们就使用 Python 实现吧！

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

class LogisticRegression:
    
    def __init__(self, w_init=0.0, steps=10000, eta=0.01):
        
        # 训练迭代次数
        self.steps = steps
        
        # 学习率
        self.eta = eta
        
        # 初始化模型参数
        self.w_init = w_init
        
        self.w = None
    
    def __z(self, X):
        '''
        计算 x 与 w 的内积
        '''
        # 矩阵点积：[1*n] ? [n*m] = [1*m]
        return np.dot(self.w, X.T)
    
    def __sigmoid(self, z):
        '''
        Sigmoid 函数
        '''
        return 1. / (1. + np.exp(-z))
    
    def __predict_proba(self, X):
        '''
        预测为正例的概率
        '''
        
        # 求 z
        z = self.__z(X)
        
        # 利用 Sigmoid 函数求预测为 '分类1' 的概率，>=0.5 的为 '分类1' ，否则为 '分类0'
        return self.__sigmoid(z)
    
    def __loss(self, y, y_pred):
        '''
        求损失
        '''
        # 数学公式见上述
        return -np.sum(y * np.log(y_pred) + (1-y)* np.log(1-y_pred)) / y.size
    
    def __preprocess(self, X):
        '''
        预处理 x，x0 = 1
        '''
        m, n = X.shape
        
        # 初始化新矩阵
        X_ = np.zeros((m, n+1))
        # x0 = 1
        X_[:, 0] = 1
        X_[:, 1:] = X
        return X_
    
    def __gradient(self, X, y, y_pred):
        '''
        求梯度
        '''
        # 矩阵乘法：[1*m] * [m*n] = [1*n]
        return np.matmul(y_pred-y, X) / y.size
        
    def train(self, X, y):
        
        # 预处理 X
        X = self.__preprocess(X)
        
        # 生成 w 矩阵
        m, n = X.shape
        self.w = np.full((1, n), self.w_init)
        
        # 创建 step-loss DataFrame，用于绘图
        plot_loss = pd.DataFrame(columns=['step', 'loss'])
        
        for step in range(1, self.steps+1):
            
            # 求 y_hat
            y_pred = self.__predict_proba(X)
            
            # 求损失，存入 DataFrame 中，并输出
            loss = self.__loss(y, y_pred)
            plot_loss.loc[plot_loss.shape[0]+1] = [step, loss]
            
            print('\rEpoch: {} {:>.2f}%: [{}{}] loss={:>.2f}'.format(
                step, step / self.steps * 100,
                '■' * int(step / self.steps * 20),
                '□' * (20 - int(step/self.steps*20)),
                loss
            ), end='')
            
            # 求梯度
            grad = self.__gradient(X, y, y_pred)
            
            # 更新权重 w
            self.w -= self.eta * grad
        
        # 绘制 step-loss 折线图
        plt.plot(plot_loss['step'], plot_loss['loss'])
        plt.xlabel('step')
        plt.ylabel('loss')
        plt.show()
    
    def predict(self, X):
        
        # 预处理 X
        X = self.__preprocess(X)
        # 求 y_hat
        y_pred = self.__predict_proba(X)
        # 转标签
        return np.where(y_pred >= 0.5, 1, 0)

测试一下，训练集就取 $x\in [0,10]$，0.1 为步长的 等差数列，$y\in 0,1$ 的二分类数组，将 $x\ge 5$ 的数据对应的标签设置为 1 ，其余为 0，弄好以后画个图瞅瞅。代码如下：

train_x = np.arange(0, 11, 0.1).reshape(-1, 1)
train_y = np.where(train_x > 5, 1, 0).reshape(1, -1)

# x = [m*n] = [110*1]，即有 110 个 x，每个 x 的维度为 1
# y = [1*m] = [1*110]，即有 110 个 y

# 显示网格线
plt.grid()
plt.plot(train_x, train_y[0])
plt.show()

折线图如下

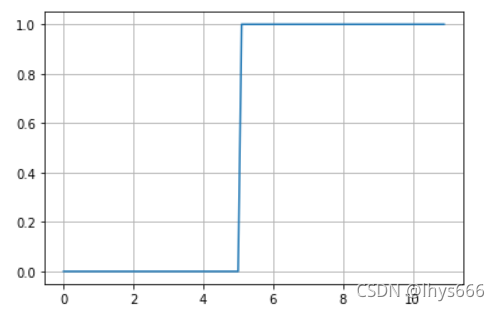
下边就用我们的模型试一试效果

model = LogisticRegression()
model.train(train_x, train_y)

可以看到，损失是逐渐 下降 的。

让我们来预测一波试试。

In[]:	model.predict(np.array([[2], [3], [4], [5], [6]]))

-------------------------------------------------------------

Out[]:	array([[0, 0, 0, 1, 1]])

看起来结果还是不错的。

利用 sklearn 实现

不得不佩服强大的 Python 生态，有好多大佬们写好的库，我们直接调用其中的 API 即可，sklearn 就是 Python 机器学习 一个常用的库，用它实现 Logistic 回归，代码如下（数据还是上边的数据）：

In[]:	from sklearn.linear_model import LogisticRegression
		lr = LogisticRegression()
		lr.fit(train_x, train_y.reshape(-1, 1))
		lr.predict(np.array([[2], [3], [4], [5], [6]]))

---------------------------------------------------------------

Out[]:	array([0, 0, 0, 1, 1])

成功咯！！！

参考资料

这可不能忘

[1]刘硕.Python机器学习算法原理、实现与案例[M].北京:清华大学出版社,2019

结尾

有想要一起学习 python 的小伙伴可以扫码进群哦。

以上就是我要分享的内容，因为学识尚浅，会有不足，还请各位大佬指正。
有什么问题也可在评论区留言。