神经网络算法-论证单层感知器的局限性
今天课上学习了一个思路 将真值表转换到平面直角坐标系中 来论证线性可分还是不可分,挺有意思记录一下。
简单感知器模型实际上仍然是MP模型的结构,但是它通过采用监督学习来逐步增强模式划分的能力,达到所谓学习的目的。
感知器处理单元对n个输入进行加权和操作v即:
v
i
=
f
(
∑
i
=
0
N
w
i
x
i
?
θ
)
v_{i}=f(\sum_{i=0}^Nw_{i}x_{i}-\theta)
vi?=f(∑i=0N?wi?xi??θ)

其中,Wi为第i个输入到处理单元的连接权值,f为阶跃函数。
感知器在形式上与MP模型差不多,它们之间的区别在于神经元间连接权的变化。感知器的连接权定义为可变的,这样感知器就被赋予了学习的特性。
利用简单感知器可以实现逻辑代数中的一些运算。
| x1 | x2 | y=x1 and x2 | y=x1 or x2 | x1取非 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 |
Y=f(w1x1+w2x2-θ)
(1)“与”运算。当取w1=w2=1,θ=1.5时,上式完成逻辑“与”的运算。
(2)“或”运算, 当取wl=w2=1,θ=0.5时,上式完成逻辑“或”的运算。
(3)“非”运算,当取wl=-1,w2=0,θ=-1时.完成逻辑“非”的运算。
与许多代数方程一样,上式中不等式具有一定的几何意义。
对于一个两输入的简单感知器,每个输入取值为0和1,如上面结出的逻辑运算,所有输入样本有四个,记为(x1,x2):(0,0),(0,1),(1,0),(1,1),构成了样本输入空间。例如,在二维平面上,对于“或”运算,各个样本的分布如下图所示。
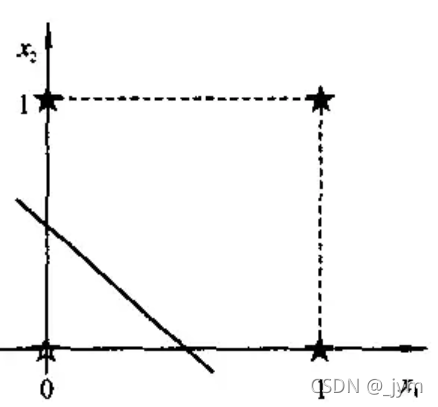
直线1 *x1+1 *x2-0.5=0将二维平面分为两部分,上部为激发区(y,=1,用★表示),下部为抑制区(y=0,用☆表示)。
简单感知器引入的学习算法称之为误差学习算法。该算法是神经网络学习中的一个重要算法,并已被广泛应用。
现在来论证一下单层感知器的局限性——仅对线性可分问题具有分类能力:
异或逻辑的真值表:
| 输入x1 | 输入x2 | 输出Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
将他们标在平面坐标系中可发现,任何直线也不能把两类样本分开。
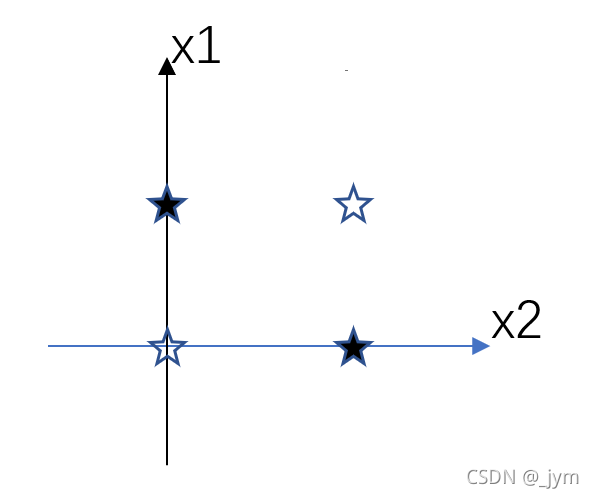
如果两类样本可以用直线、平面或者超平面分开,称为线性可分,否则为线性不可分。
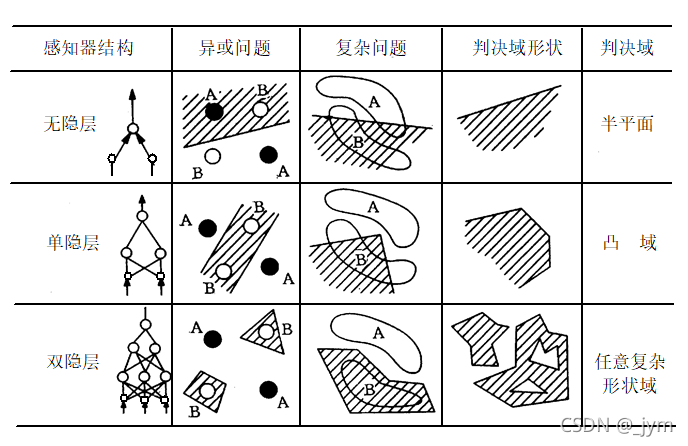
所以说要克服单层感知器这一局限性
就需要在输入层与输出层之间引入隐层作为输入模式的内部表示。