一:DNN的反向传播算法
我们在监督学习中的一般问题是,假设我们有m个训练样本,{(x1,y1),(x2,y2),…,(xm,ym)},其中x是输入维度,输入特征维度为n_in,y为输出向量,输出的特征唯独为n_out,.我们需要利用这m个训练样本训练出一个模型,以便于在一个新的输入向量输入后,经过模型计算,可以预测y向量的输出。
那么在Dnn中,我们使输入层有n_in个输入神经元,输出层有n_out个神经元。再加上若干个隐藏层神经元,此时我们需要找到适合所有隐藏层和输出层的线性权重系数矩阵W和偏置b,让所有训练样本输入计算出的输出尽可能的接近真实样本的输出。怎么找出这些系数是关键。
在传统的机器学习中我们的办法是,使用一个合适的损失函数来度量模型的输出损失,我们通过优化损失函数求最小化的极值,在此极值条件下得到的一系列的w和b就是我们想要的。在dnn中,损失函数优化求极值的过程我们一般采用梯度下降的方法来一步步迭代完成。
对DNN的损失函数用梯度下降法进行迭代优化求极小值的过程即为我们的反向传播算法。
二. DNN反向传播算法的数学推论。
在进行DNN反向传播算法前,我们需要选择一个损失函数,来度量训练样本计算出的输出和真实的训练样本输出之间的损失。你也许会问:训练样本计算出的输出是怎么得来的?这 个输出是随机选择一系列W,b,用我们上一节的前向传播算法计算出来的。即通过一系列的计算:
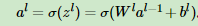
计算到输出层第L层对应的aL即为前向传播算法计算出来的输出。
DNN的损失函数有很多,我们这里为了方便求偏导,采用均方误差来度量输出损失。即对每个样本,我们希望最小化下式:
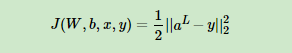
其中,aL和y为特征维度为n_out的向量,|| |2为L2范数。
损失函数有了,现在我们开始用梯度下降法迭代求解每一层的W,b。
首先是输出层第L层。注意到输出层的W,b满足下式:
|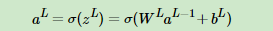
这样对于输出层的参数,我们的损失函数变为:
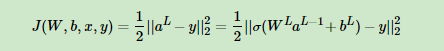
根据上面损失函数,我们就可以求解W和b的梯度了:
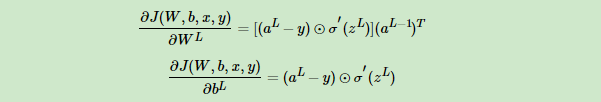
注意上式中有一个符号⊙,它代表Hadamard积,对于两个维度相同的向量A(a1,a2,…an)T和B(b1,b2,…bn)T,则A⊙B=(a1b1,a2b2,…anbn)T。
我们注意到在求解输出层的W,b的时候,有中间依赖部分:
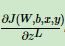
因此我们可以把公共的部分即对zL先算出来,记为:
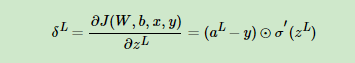
现在我们终于把输出层的梯度算出来了,那么如何计算上一层L?1层的梯度,上上层L?2层的梯度呢?这里我们需要一步步的递推,注意到对于第l层的未激活输出zl,它的梯度可以表示为:
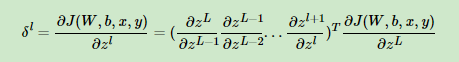
如果我们可以依次计算出第l层的δl,则该层的Wl,bl很容易计算?为什么呢?注意到根据前向传播算法,我们有:
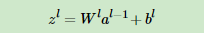
所以根据上式我们可以很方便的计算出第l层的Wl,bl的梯度如下:
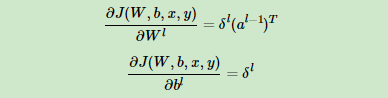
那么现在问题的关键就是要求出δl了。这里我们用数学归纳法,第L层的δL上面我们已经求出, 假设第l+1层的δl+1已经求出来了,那么我们如何求出第l层的δl呢?我们注意到:
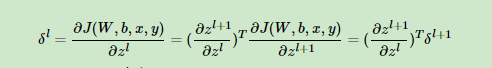
可见,用归纳法递推δl+1和δl的关键在于求解αz l+1/αzl
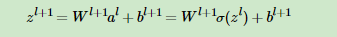
这样很容易求出:
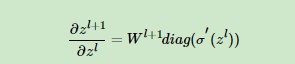
将上式带入上面δl+1和δl关系式我们得到:
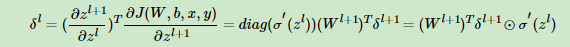
现在我们得到了δl的递推关系式,只要求出了某一层的δl,求解Wl,bl的对应梯度就很简单的。
三:DNN反向传播算法实现步骤
现在我们总结下DNN反向传播算法的过程。由于梯度下降法有批量(Batch),小批量(mini-Batch),随机三个变种,为了简化描述,这里我们以最基本的批量梯度下降法为例来描述反向传播算法。实际上在业界使用最多的是mini-Batch的梯度下降法。不过区别仅仅在于迭代时训练样本的选择而已。
输入: 总层数L,以及各隐藏层与输出层的神经元个数,激活函数,损失函数,迭代步长α,最大迭代次数MAX与停止迭代阈值?,输入的m个训练样本{(x1,y1),(x2,y2),…,(xm,ym)}
- 初始化各隐藏层与输出层的线性关系系数矩阵W和偏倚向量b的值为一个随机值。输出:各隐藏层与输出层的线性关系系数矩阵W和偏置向量b
2)for iter to 1 to MAX:
2-1) for i =1 to m:
a) 将DNN输入a1设置为xi
b) for l=2 to L,进行前向传播算法计算公式计算
c) 通过损失函数计算输出层的δi,L
d) for l= L-1 to 2, 进行反向传播算法计算公式计算
2-2) for l = 2 to L,更新第l层的Wl,bl:
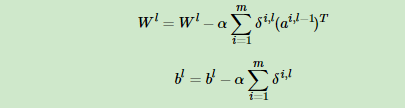
2-3) 如果所有W,b的变化值都小于停止迭代阈值?,则跳出迭代循环到步骤3
3) 输出各隐藏层与输出层的线性关系系数矩阵W和偏倚向量b。
四:DNN反向传播算法小结
有了DNN反向传播算法,我们就可以很方便的用DNN的模型去解决第一节里面提到了各种监督学习的分类回归问题。当然DNN的参数众多,矩阵运算量也很大,直接使用会有各种各样的问题。有哪些问题以及如何尝试解决这些问题并优化DNN模型与算法,我们在下一篇讲,当然本章未完待续,本文主要参考刘建平老师的该文章,接下来,作者会根据自己的经验和知识来进行完善