机器学习通俗理解系列
关于knn的通俗理解.
前言
??刚学习机器学习的时候免不了百度,问什么是K-means?所以此刻你将看到的是K-means的通俗说明,带你快速理解K-means原理以及应用
一、什么是K-means?
??k均值聚类算法(k-means clustering algorithm)简称K-means,属于无监督聚类算法,其作用通俗来说给定一个数据点集合和需要的聚类数目k,k由用户指定,k均值算法根据某个距离函数反复把数据分入k个聚类中,机器学习常用算法之一,你,值得拥有!ps:不懂有监督和无监督区别请移步
二、什么原理?
官方说明:先随机选取K个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了,每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。
通俗理解:简单来说设K值,1.随机初始K个聚类中心,2.计算所有点对每个中心距离,对比划分到距离自己最近的那个中心,形成K个簇后,3.再重新计算每个簇中心,重复2.3步骤直到中心点不变化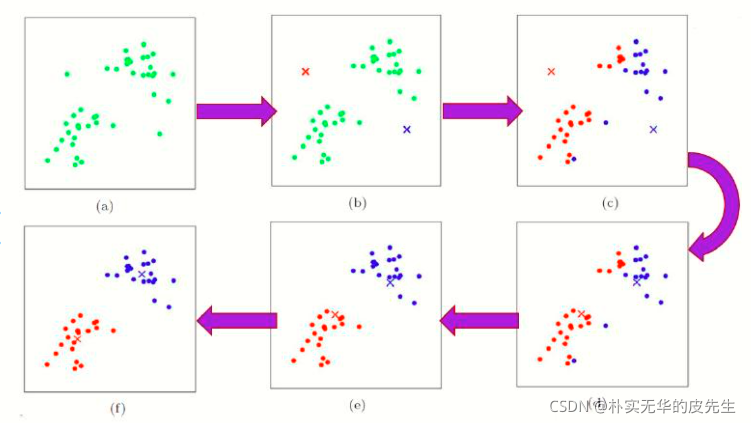
流程
(1)选择聚类的个数k(kmeans算法传递超参数的时候,只需设置最大的K值)
(2)将样本集按照最小距离原则分配到最邻近聚类形成k个簇;
(3)使用每个聚类的样本均值更新聚类中心;
(4)重复步骤(2)、(3)直到聚类中心不再发生变化;
(5)输出最终的聚类中心和k个簇划分;
三、重点
??细节上我们需要知道
1、K值的选定
对于二维的数据,我们还能通过肉眼观察法进行确定,超过二维的数据怎么办?
-
拍脑袋法
将样本量除以2再开平方出来的值作为K值,具体公式为:
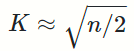
-
肘部法则
此种方法适用于 K 值相对较小的情况,当选择的k值小于真正的时,k每增加1,cost值就会大幅的减小;当选择的k值大于真正的K时, k每增加1,cost值的变化就不会那么明显。这样,正确的k值就会在这个转折点,类似elbow的地方。具体公式:
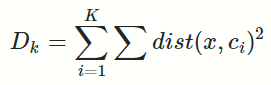

-
间隔统计量
-
轮廓系数
-
Canopy算法
ok这里只做前两个了解,感兴趣的朋友可自行深入了解哈。详情可见:链接: https://www.biaodianfu.com/k-means-choose-k.html.
2、样本之间的距离
闵可夫斯基距离/欧氏距离(多维)
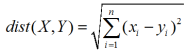
四、优缺点
优点:
1、原理比较简单,实现也是很容易,收敛速度快。
2、聚类效果较优。
3、算法的可解释度比较强。
4、主要需要调参的参数仅仅是簇数k。
缺点:
1、受初始值和异常点影响,
2、聚类结果可能不是全局最优而是局部最优
3、样本点只能划分到单一的类中
4、算法时间复杂度比较高
五、优化进阶
优化算法:k-Means++
??k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响,因此需要选择合适的k个质心。如果仅仅是完全随机的选择,有可能导致算法收敛很慢。K-Means++算法就是对K-Means随机初始化质心的方法的优化
1.从样本中选择 1 个点作为初始质心(完全随机)
2.对于任意一个非质心样本 x,计算x与现有最近质心距离 D(x)
3.基于距离计算概率,来选择下一个质心 x,选择距离当前质心远的点作为质心
4.重复步骤 2 与 3 ,直到选择 k 个质心为止。
优化算法:elkan K-Means
??利用了两边之和大于等于第三边,以及两边之差小于第三边的三角形性质,来减少距离的计算
大样本优化Mini Batch K-Means
样本集中的一部分的样本来做传统的K-Means,代价就是我们的聚类的精确度也会有一些降低,多跑几次Mini Batch K-Means算法,用得到不同的随机采样集来得到聚类簇,选择其中最优的聚类簇。
总结:
??如此大家也就能够通俗的理解K-means大致原理了。这里只做一个快速理解系列,若要详细学习可不要偷懒哟。