前言

看了李沐老师的动手深度学习其代码来自第二版，3.1

https://zh-v2.d2l.ai/chapter_linear-networks/linear-regression.html

，最近有一点想法记录一下。手撸SGD,等方式的区别。

一、固定随机数

这步骤用来复现结果

#结果可复现 设置随机数种子
def setup_seed(seed):
    torch.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    torch.backends.cudnn.deterministic = True


# 设置随机数种子
setup_seed(20)

二、生成数据集

#生成数据
def synthetic_data(w, b, num_examples):  #@save
    """生成 y = Xw + b + 噪声。"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

plt.scatter(features[:,1],labels)
plt.show()

应该得到形如如下的数据：
数据分布

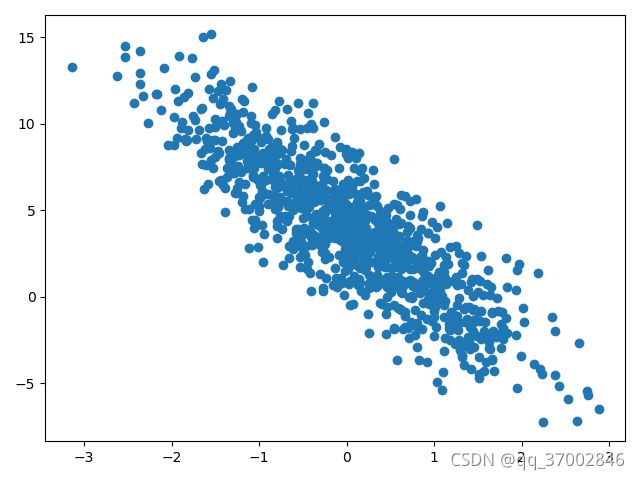
三、初始化参数

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)#tensor([[0.0033],[0.0007]], requires_grad=True) 
b = torch.zeros(1, requires_grad=True)#tensor([0.], requires_grad=True)

定义函数

def linreg(X, w, b):  #@save
    """线性回归模型。"""
    return torch.matmul(X, w) + b

定义损失

def squared_loss(y_hat, y):  #@save
    """均方损失。"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

四、sgd

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降。"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

五、实验

这个地方是重点，有些不明白的地方可以根据简单的实验清楚。

lr = 0.0003
num_epochs = 300
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # `X`和`y`的小批量损失
        # 因为`l`形状是(`batch_size`, 1)，而不是一个标量。`l`中的所有元素被加到一起，
        # 并以此计算关于[`w`, `b`]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

结果：

epoch 300, loss 0.000049
w的估计误差: tensor([ 0.0004, -0.0008], grad_fn=<SubBackward0>)
b的估计误差: tensor([0.0008], grad_fn=<RsubBackward1>)

问题1：为什么loss不为0？
首先，通过相关的数学概念，我们知道在神经网络中，loss是可以为0的。
看下面一个简单的例子：
我们要学习到 w=1 即 y=x，
输入的特征是0,1,2,3，输出的标签是0,1,2,3.

simple_feature=torch.tensor([0,1,2,3])
simple_labels=torch.tensor([0,1,2,3])
simple_w=torch.tensor([2],requires_grad = True,dtype = torch.float)
simple_turew=torch.tensor([1])
def simple_linreg(X,w):
    return X*w

lr = 0.3
num_epochs = 300
def simple_squared_loss(y_hat, y):  #@save
    """均方损失。"""
    #print("y:hat",y_hat)
    #print("y:",y)
    return (y_hat - y) ** 2
loss = simple_squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(1, simple_feature, simple_labels):
        l = loss(simple_linreg(X,simple_w), y)  # `X`和`y`的小批量损失
        # 因为`l`形状是(`batch_size`, 1)，而不是一个标量。`l`中的所有元素被加到一起，
        # 并以此计算关于[`w`, `b`]的梯度
        l.sum().backward()
        sgd([simple_w], lr, batch_size)  # 使用参数的梯度更新参数
        with torch.no_grad():
            train_l = loss(simple_linreg(simple_feature, simple_w), simple_labels)
            print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
print(simple_w)
print(f'w的估计误差: {simple_turew - simple_w}')

在第8个epoch就可以收敛到0

epoch 1, loss 2.021600
epoch 1, loss 2.021600
epoch 1, loss 0.427771
epoch 1, loss 0.377978
epoch 2, loss 0.333982
epoch 2, loss 0.333982
epoch 2, loss 0.070670
epoch 2, loss 0.040819
epoch 3, loss 0.008637
epoch 3, loss 0.004989
epoch 3, loss 0.004408
epoch 3, loss 0.004408
epoch 4, loss 0.003895
epoch 4, loss 0.002250
epoch 4, loss 0.000476
epoch 4, loss 0.000476
epoch 5, loss 0.000476
epoch 5, loss 0.000101
epoch 5, loss 0.000089
epoch 5, loss 0.000051
epoch 6, loss 0.000045
epoch 6, loss 0.000026
epoch 6, loss 0.000026
epoch 6, loss 0.000006
epoch 7, loss 0.000006
epoch 7, loss 0.000005
epoch 7, loss 0.000001
epoch 7, loss 0.000001
epoch 8, loss 0.000000
tensor([1.], requires_grad=True)
w的估计误差: tensor([0.], grad_fn=<SubBackward0>)

那么什么情况不会收敛，这个欢迎大家指出：
1）错误标签。也可以说是噪声。
只要把上面的改为

simple_feature=torch.tensor([0,1,2,3])
simple_labels=torch.tensor([0,1,2,3.1])

就会得到下面神奇的情况，就是我跑了30000个epoch 损失还是不为零。可想而知，无论每日每夜的算下去，都不会得到w=1的结果。因为数据中有噪声。

epoch 30000, loss 0.000986
tensor([1.0266], requires_grad=True)
w的估计误差: tensor([-0.0266], grad_fn=<SubBackward0>)

2）网络参数不够
还是上面这个例子，有人说，是模型太简单了，数据没问题。
那么可以加个参数试试，把上面的简单的线性变换加上有偏置的

def simple_linreg(X,w,b):
    return torch.matmul(X, w)+b

epoch 30000, loss 0.000848
tensor([1.0359], requires_grad=True)
w的估计误差: tensor([-0.0359], grad_fn=<SubBackward0>)

结果还是不行，似乎简单的线性方程无法拟合。那么用非线性的方式,加一个非线性的激活函数解决：

def simple_non_linearity(x):

    for i in range(0,x.size(0)):
        if(x[i]>=3):
            x[i]+=0.1
    return x
for epoch in range(num_epochs):
    for X, y in data_iter(1, simple_feature, simple_labels):
        l = loss(simple_non_linearity(simple_linreg(X,simple_w)), y)  # `X`和`y`的小批量损失
        # 因为`l`形状是(`batch_size`, 1)，而不是一个标量。`l`中的所有元素被加到一起，
        # 并以此计算关于[`w`, `b`]的梯度
        l.sum().backward()
        sgd([simple_w], lr, batch_size)  # 使用参数的梯度更新参数
        with torch.no_grad():
            train_l = loss(simple_non_linearity(simple_linreg(simple_feature, simple_w)), simple_labels)
            print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
print(simple_w)
print(f'w的估计误差: {simple_turew - simple_w}')

epoch 1, loss 2.035564
epoch 1, loss 2.035564
epoch 1, loss 0.414369
epoch 1, loss 0.366136
epoch 2, loss 0.323518
epoch 2, loss 0.323518
epoch 2, loss 0.068456
epoch 2, loss 0.039540
epoch 3, loss 0.008367
epoch 3, loss 0.004833
epoch 3, loss 0.004270
epoch 3, loss 0.004270
epoch 4, loss 0.003773
epoch 4, loss 0.002179
epoch 4, loss 0.000461
epoch 4, loss 0.000461
epoch 5, loss 0.000461
epoch 5, loss 0.000098
epoch 5, loss 0.000086
epoch 5, loss 0.000050
epoch 6, loss 0.000044
epoch 6, loss 0.000025
epoch 6, loss 0.000025
epoch 6, loss 0.000005
epoch 7, loss 0.000005
epoch 7, loss 0.000005
epoch 7, loss 0.000001
epoch 7, loss 0.000001
epoch 8, loss 0.000000
损失的变化和上面的不一样，是因为定义的激活函数，改变了值。