代码：https://github.com/jindongwang/transferlearning/tree/master/
code/deep/adarnn
1. 引文
文章提出了一个总体框架AdaRNN，该框架通过提出时间分布表征和时间分布匹配算法来学习准确的、自适应的模型。
主要由两部分组成：
1.时域分布特征化(TDC): 目的是更好地描述时间序列中的分布信息。根据最大熵原理，将训练数据分解为𝐾个分布差距大的最不同时段。
2.时域分布匹配(TDM)：旨在减少时间序列中的分布不匹配，学习一种基于RNN的自适应时间序列预测模型。主要是基于RNNs去动态减小分布散度
时序预测的方法包括：隐式马尔科夫，动态贝叶斯网络，卡尔曼滤波器，循环神经网络
难点：
1.时序数据的非稳定性使得数据分布时刻变化。数据分布P(x)在不同时间区间是变化的，而条件分布P(y|x)在某一场景下是固定的，如在股票预测中，金融因素x会随着市场变动而改变，但是背后的经济规律P(y|x)是不变的。
2.因为本案例分布改变的问题违背了上述模型的独立同分布的准则，使得上述模型的效果和泛化性都很差。
从分布的角度建模时间序列仍然没有被探索。这个问题的主要挑战在于两个方面：
1.首先，如何描述数据中的分布，以最大限度地利用这些不同分布中的共有知识?
2.如何创造一种基于RNN的分布匹配算法，在捕获时间依赖性的同时最大限度地减少它们的分布差异?
2. 相关研究：
传统的时间序列分类或回归方法包括基于距离的、基于特征的和集成学习方法。
- 基于距离的方法用一些度量，如欧氏距离或动态时间规划(DTW)，来度量原始序列数据(段)的距离和相似性。
- 基于特征的方法依靠一组人工提取或学习的特征来捕获时间序列中的全局/局部模式。
- 集成方法结合多个弱分类器来提高模型的性能。
然而，在数据预处理和特征工程(data pre-processing and labor-intensive feature)中涉及大量的人工操作，使得这些方法难以处理大规模数据，对于更复杂的模式，性能也受到限制。GRUs和LSTM由于能够自动提取高质量的特征并处理长期依赖关系而受到广泛应用。这些深度方法通过利用注意机制或张量分解来捕获序列之间的共享信息来处理TS分类或预测。
时间序列分割和聚类是两个与本文的时间分布特征相似的主题。时间序列分割的目的是将时间序列分割成若干块，用于发现其背后的模式;它主要采用变点检测算法，包括滑动窗口法、自底向上法和自顶向下法。现有的分割方法几乎没有采用分布匹配方案，不能适应我们的问题。而时间序列聚类的目的是寻找由相似(段)时间序列组成的不同组，这与我们的情况明显不同。
当训练和测试数据来自不同的分布时，通常的做法是采用一些域自适应(DA)算法来弥补它们的分布差距，这样就可以学习域不变表示。DA经常对训练和测试数据进行实例重加权或特征转移，以减少分布发散。与一般方法中的DA相似，域泛化(DG)也在多个源域上学习域不变模型，希望它能很好地泛化到目标域。DA和DG之间的唯一区别是DA假设测试数据是可访问的，而DG则不是。很明显，我们的问题设置与DA和DG不同。首先，由于域在问题中具有先验性，DA和DG没有建立时间分布表征。其次，大多数数据同化和DG方法都是利用CNN而不是RNNs进行分类。因此，它们可能无法捕捉到时间序列中的长期时间依赖性。
3. 概念定义：
- Covariate Shift 协变量转变：给定两个不同分布
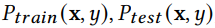的训练集和测试集，协变量转变是指边缘分布不同，而条件概率分布相同的情况，即 
-
?注意，协变量移位的定义是针对非时间序列数据的。现在我们将它的定义扩展到时间序列数据，在本工作中称为时间协变量移位(TCS)。
-
covariate shift problem时间协变量移位：给定有n个已标记的时间分段的序列
，
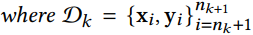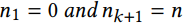。时间协变量移位指的是在同一个时间段i的所有时间点都符合同样的数据分布
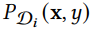，而不同时间段之间
，
?要学习TCS下具有良好泛化性能的预测模型，一个关键的研究问题是获取
不同时期的共同知识。例如股票预测即使金融因素随着市场变化而变化，但是一些共同的知识，如经济规律和模式即
，依然能被用于精确预测。
但是TCS的时段数K和每个时段的界限依旧未知。因此，在设计一个模型来捕捉训练中不同时段之间的共性之前，我们需要首先通过比较它们的底层数据分布来发现时段，使同一时段的段遵循相同的数据分布。本文研究问题的形式化定义如下。
我们的目标是自动发现训练时间序列数据中的𝐾时段，并通过挖掘不同时段之间的共性来学习一个预测模型M: x𝑖→y𝑖，从而对未来的𝑟个时间点
进行精确预测。在这里我们假设测试部分是在同一时间段。简述为以下：
?
学习训练时间序列数据下的周期是具有挑战性的，因为周期的数量和相应的边界都是未知的，而且搜索空间是巨大的。然后，在确定了周期后，下一个挑战是如何学习一个好的可推广的预测模型
用于未来的周期。如果不能准确地发现周期，可能会影响最终预测模型的泛化性能。
4. 本文方法详述
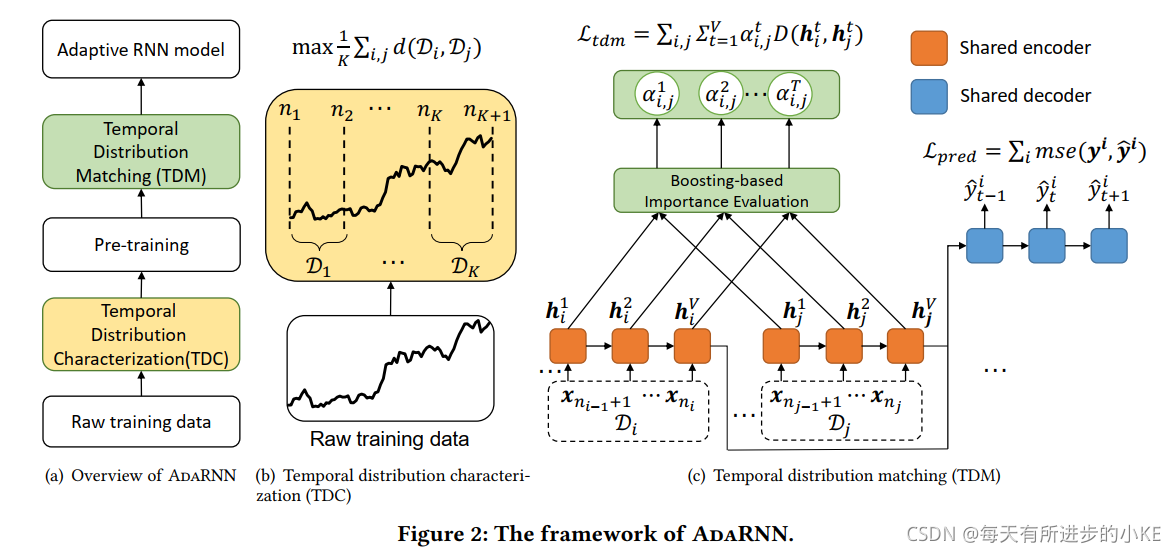
?提出的AdaRNNs主要用于解决时域协变量转变的问题，如图2，主要由两种方法组成：时域分布特征化(TDC)和时域分布匹配(TDM)。对于训练数据，AdaRNN首先利用TDC将其划分为充分表征其分布信息的时间段。然后利用TDM模块进行周期间的分布匹配，建立广义预测模型M，用新数据的r步预测。
AdaRNN的基本原理如下。在TDC中，模型M被期望在最坏的分布情况下工作，在这种情况下，不同时期之间的分布差距很大，因此可以通过最大化它们的差异来确定最优的时间段分割。在TDM中，M利用学习到的时间段的共同知识，通过RNNs与正则化项匹配它们的分布，从而做出精确的未来预测。
4.1 时域分布特征化
?根据最大熵[17]原理，最大限度地利用时间协变移位下的时间序列的共享知识可以通过寻找彼此最不相似的时间段来实现，这也被认为是时间协变量移位的最坏情况，因为跨时间段分布是最多样化的。因此，如图2(b)所示，TDC通过求解一个优化问题来实现TS拆分的目标，其目标可以表示为:
?其中d是一个距离度量，可以是欧几里德或编辑距离，或一些基于分布的距离/散度，如MMD[14]和KL-divergence。
是避免平凡解的参数，而K0是为了避免过度分段。
第一个问题是寻找时段数K和对应的时段使得时段平均分布距离最大化，从而使得模型具有较好的泛化性。
我们利用最大化熵值(ME)的原则来解释分割场景，即为何我们需要差异最大的时段？根据ME理论，在对时间序列数据的分割没有预先假设的情况下，每个时段的分布尽可能的多样化是合理的，以最大限度地提高总分布的熵。这允许对未来数据进行更通用和灵活的建模。因此，由于我们对测试数据没有先验信息，训练时这些信息也是未知的，所以在最坏的情况下训练一个模型更合理，可以使用不同的时段分布进行模拟。如果模型能在最坏的情况进行学习，那它能更好地对未知的测试数据有更好的泛化性能，多样性在TS建模有着重要作用。
具体来说，(1)中的时间序列分割是计算复杂的，并且可能无更紧凑的形式。为了选择合适的度量距离，这个优化问题可以利用动态规划的方式解决。在本工作中，考虑到大规模数据的可扩展性和效率问题，我们采用贪婪算法求解(1)。具体来说，为了更有效率的计算以及避免平凡解，我们将时序平均分成N=10个部分，每一部分是不能再分割的最小单位周期。我们从{2,3,5,7,10}随机寻找K值。给定K，基于贪婪算法长度为nj的时段，将时序的开端和末端定义为A和B，考虑K=1,我们只需要从9个候选点中得到一个分离点C，从而使得分布距离
能够最大化。在C被确定后，考虑K=3，使用相同的策略得到D点，以此类推得到其他K值的分离点。实验结果证明相比于随机分割，贪婪算法能够选取更合适的时段。同时，也说明当K非常大或非常小时，预测模型的最终结果都很差。
4.2 时域分布匹配
给定上述方法得到的分离时段，TDM模块的设计是通过匹配不同时期的分布来学习不同时期所共有的知识。因此，与仅依赖局部或统计信息的方法相比，学习后的模型M有望在未知测试数据上有较好的泛化效果。TMD预测结果的Loss值
定义为：
?其中
时模型学习的参数。
然而，最小化(2)只能学习每个时间段的预测知识，不能减少不同时间段的分布差异进而利用公共知识。一个实用的方法是通过采用一些最常见的分布匹配距离作为正则化器去匹配每个时间段
的分布。从域适应的相关工作可知，分布匹配通常有高水平的表达，我们将分布匹配正则化项应用于RNN模型单元的最终输出。形式上，我们使用
表示RNN 的V个隐藏层输出的q维度特征。然后，对(D𝑖，D𝑗)的最终隐藏状态的周期分布匹配可以表示为：
?不幸的是，上述正则化项未能捕获RNN中每个隐藏状态的时间依赖性。由于每个隐藏状态只包含输入序列的部分分布信息，在构造分布匹配正则化器时需要考虑RNN的每个隐藏状态，如下节所述。
?4.2.1 时域分布匹配
如图2(c)，我们提出TDM去适时地匹配某两个时段分布的RNNs的输出，以此获取时域的依赖性。TDM引入重要性向量𝜶∈R^𝑉来学习RNNs V个隐藏层状态的相对重要程度,其中所有隐藏状态都用一个归一化的𝜶进行加权。请注意，对于每对时段，都有一个𝜶，如果没有混淆，则省略下标。利用这种方式我们能动态地降低时段之间地分布散度。
给定一对(D𝑖, D𝑗 )，时域分布匹配的loss可以描述为：
RNN的所有隐藏状态都可以很容易地通过遵循标准的RNN算法得到。用𝛿(·)表示基于前一个状态的下一个隐藏状态的计算。状态计算可以表示为：
?将(2)与(3)整合，时间分布匹配(单层RNN)的最终目标为:
?（
= 1/(A^2_6))。这里𝜆是一个权衡超参数。注意，在第二项中，我们计算所有时段对的分布距离的平均值。为了计算，我们取一小批D𝑖和D𝑗在RNN层中进行前向运算，并连接（加权求和）所有隐藏特征。然后，我们可以使用(5)执行TDM。
4.2.2 基于增强学习(Boosting-based)重要性的评估
我们提出了一个基于boost的重要性评估算法来学习𝜶。在此之前，我们首先使用所有时段的全标记数据对网络参数𝜃进行预训练，即使用(2)。这是为了学习更好的隐藏状态表示，以便于𝜶的学习。
我们将预先训练的参数表示为
通过,TDM使用了一个基于增强学习的过程来学习隐藏状态的重要性。最初，对于每个RNN层，所有权值都初始化为同一层中的相同值，即:
。我们选择跨域分布距离作为boosting的指标。当第n+1次 epoch的分布散度大于第n次epoch时，我们增大
来增强其作用效果从而减小分布散度；否则，保持不变。这种增强学习表示为:
?(7)式是根据不同学习阶段的分布匹配损失来计算的更新函数。并且
为第n个epoch中𝑡时间步处的分布距离。𝜎(·)为sigmoid函数。我们也要对权重参数进行归一化：
。通过(3)和(6),我们能得到𝜶的值
备注1：目标(3)定义在一个RNN层上，也可以方便地对多个层进行实现，实现多层分布匹配。至于推断，我们只需使用最优网络参数𝜃?。
备注2：为了得到𝜶，也有一种网络被提出，其输入为
，输出为𝜶，权重为
。例如，𝜶能够以下得到：
?然而，上面的方法存在两个问题：首先，因为𝜶𝑖,𝑗 和𝜃是高度相关的，并且在早期训练阶段，𝜃意义不大，将会导致𝜶𝑖,𝑗的不充分学习。其次，基于RNN模型学习每对域的
是比较费时的。
4.3 分布距离的计算
分布距离，即函数𝑑(·，·)，从技术上讲，TDC中的𝑑(·，·)和TDM中的𝑑(·，·)可以是相同的选择。我们采用几种常用的距离:余弦距离，MMD[14]和对抗距离[12]。还要注意，TDC和TDM目前是控制计算复杂度的两个独立阶段。对这两个阶段进行端到端优化将是未来的工作。算法1给出了AdaRNN的完整过程。这些距离的具体实现在附录中给出。
