一、岭回归

（一）解决的问题

1、自变量个数多于样本量

2、存在多重共线性

（二）解决方法

在线性回归模型的目标函数上添加一个 $l2$ 的正则项(也称为惩罚项)，从而使得模型的回归系数有解

岭回归模型的目标函数表示为： $J(\beta )=\sum(y-X\beta)^{2}+\sum \lambda \beta ^{2}$

为了使目标函数达到最小，只能通过缩减回归系数使 $\beta$ 趋近于0

求目标函数最小值：先对其求导，再令导函数为0

重点：一个 $\lambda$ 对应一个 $\beta$ ，求出最优的 $\lambda$ ，使得目标函数最小，则得到相应回归系数 $\beta$

（三）python实现（k重交叉验证法确定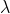 $\lambda$ 值）

import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn import model_selection
from sklearn.linear_model import Ridge,RidgeCV,Lasso,LassoCV
import matplotlib.pyplot as plt

#数据导入
dataset=pd.read_csv(r'C:\Users\DELL\Desktop\5.csv')

#---------------岭回归建模---------------#
#【交叉验证法确定lambda值】
#拆分数据集为训练集(8个样本)和测试集(3个样本)
X_train,X_test,y_train,y_test=model_selection.train_test_split(dataset[dataset.columns[1:]],dataset['y'],test_size=0.2,random_state=1234)
#构造不同的Lambda值
Lambdas=np.logspace(-5,2,100)
#设置交叉验证的参数，对于每一个Lambda值，都执行8重交叉验证
ridge_cv=RidgeCV(alphas=Lambdas,normalize=True,scoring='neg_mean_squared_error',cv=8)   #cv的值不能超过样本数量
#模型拟合
ridge_cv.fit(X_train,y_train)
#返回最佳的lambda值
ridge_best_Lambda=ridge_cv.alpha_
print('最佳的lambda值：',ridge_best_Lambda)

#【基于最佳的lambda值建模】
ridge=Ridge(alpha=ridge_best_Lambda,normalize=True)
ridge.fit(X_train,y_train)
#返回岭回归模型的回归系数
pd.Series(index=['Intercept']+X_train.columns.tolist(),data=[ridge.intercept_]+ridge.coef_.tolist())

#【模型的预测】
ridge_predict=ridge.predict(X_test)
#预测效果验证(用评估模型好坏的均方根误差RMSE)
RMSE=np.sqrt(mean_squared_error(y_test,ridge_predict))
print('岭回归的均方根误差RMSE：',RMSE)

【输出结果】

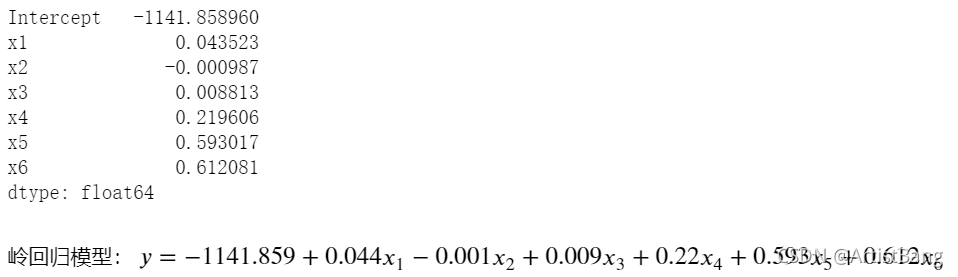
二、LASSO回归

（一）解决的问题

1、岭回归最终会保留建模时的所有变量，无法降低模型的复杂度

（二）解决方法

LASSO回归与岭回归类似，属于缩减性估计，但在回归系数的缩减过程中，可以将一些不重要的回归系数直接缩减为0，即达到变量筛选的功能（直接删除相应变量）

LASSO回归模型的目标函数表示为： $J(\beta )=\sum(y-X\beta)^{2}+\sum \lambda\left | \beta \right |$

?重点：一个 $\lambda$ 对应一个 $\beta$ ，求出最优的 $\lambda$ ，使得目标函数最小，则得到相应回归系数 $\beta$

（三）python实现（k重交叉验证法确定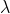 $\lambda$ 值）

#---------------LASSO回归建模---------------#
#【LASSO回归模型的交叉验证】
lasso_cv=LassoCV(alphas=Lambdas,normalize=True,cv=8,max_iter=1000)
#模型拟合
lasso_cv.fit(X_train,y_train)
#输出最佳的lambda值
lasso_best_alpha=lasso_cv.alpha_
print('最佳的lambda值：',lasso_best_alpha)

#【基于最佳的lambda值建模】
lasso=Lasso(alpha=lasso_best_alpha,normalize=True,max_iter=1000)
#对“类”加以数据实体,执行回归系数的运算
lasso.fit(X_train,y_train)
#返回Lasso回归的系数
pd.Series(index=['Intercept']+X_train.columns.tolist(),data=[lasso.intercept_]+lasso.coef_.tolist())
#由结果可知：自变量x2、x4、x5、x6对于因变量y不显著，即只有x1和x3显著

#【模型预测】
lasso_predict=lasso.predict(X_test)
#预测效果验证(用评估模型好坏的均方根误差RMSE)
RMSE=np.sqrt(mean_squared_error(y_test,lasso_predict))

【输出结果】?