开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> Image Classification ——【AlexNet】 -> 正文阅读

[人工智能]Image Classification ——【AlexNet】

强烈建议大家在读论文前先看这个视频。如何读论文【论文精读】

请添加图片描述

1 论文阅读

AlexNet论文翻译——中英文对照

1.1 论文摘要

我们训练了一个大型深度卷积神经网络来将120万高分辨率的图像分到1000不同的类别中。这个神经网络有6000万参数和650000个神经元，包含5个卷积层（某些卷积层后面带有池化层）和3个全连接层，最后是一个1000维的softmax。为了训练的更快，我们使用了非饱和神经元并对卷积操作进行了非常有效的GPU实现。为了减少全连接层的过拟合，我们采用了一个最近开发的名为dropout的正则化方法，结果证明是非常有效的。

至此，网络的功能和结构就完全被你了解，下面我们将对细节进行深入的探究。

1.2 论文创新点

① ReLU Nonlinearity ReLU非线性
将神经元输出f建模为输入x的函数的标准方式是用f(x) = tanh(x)或f(x) = (1 + e?x)?1。考虑到梯度下降的训练时间，这些饱和的非线性比非饱和非线性f(x) = max(0,x)更慢。根据Nair和Hinton[20]的说法，我们将这种非线性神经元称为修正线性单元(ReLU)。
特点：加快了训练的速度。

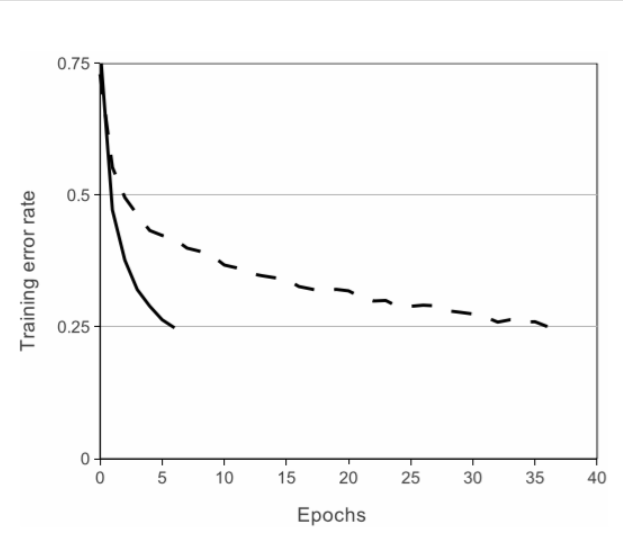在这里插入图片描述在上图中，对于一个特定的四层卷积网络，在CIFAR-10数据集上达到25%的训练误差所需要的迭代次数可以证实这一点。这幅图表明，如果我们采用传统的饱和神经元模型，我们将不能在如此大的神经网络上实验该工作。（黑线采用Relu作为激活函数）

② Training on Multiple GPUs 多GPU训练

事实证明120万图像用来进行网络训练是足够的，但网络太大因此不能在单个GPU上进行训练。因此我们将网络分布在两个GPU上。我们采用的并行方案基本上每个GPU放置一半的核（或神经元），还有一个额外的技巧：只在某些特定的层上进行GPU通信。
这意味着，例如，第3层的核会将第2层的所有核映射作为输入。然而，第4层的核只将位于相同GPU上的第3层的核映射作为输入。连接模式的选择是一个交叉验证问题，但这可以让我们准确地调整通信数量，直到它的计算量在可接受的范围内。

③ Local Response Normalization 局部响应归一化

ReLU具有让人满意的特性，它不需要通过输入归一化来防止饱和。如果至少一些训练样本对ReLU产生了正输入，那么那个神经元上将发生学习。然而，我们仍然发现接下来的局部响应归一化有助于泛化。

在这里插入图片描述

论文中给的公式时batch normalization的前身。
大概就是说relu虽然有normalization的作用，但他们还是对输入做了normalization，发现效果更好。

④ Overlapping Pooling 重叠池化
习惯上，相邻池化单元归纳的区域是不重叠的。在CNN中采用的传统局部池化，池化区域是不重叠的。例如步长是2，池化窗口是2，每次池化都不会重叠。但当步长是2，池化窗口是3，很容易去想象会有重叠。池化窗口时在训练过程中通常观察采用重叠池化的模型，发现它更难过拟合。

⑤ Dropout 失活法

这种最近引入的技术，叫做“dropout”，它会以0.5的概率对每个隐层神经元的输出设为0。那些“失活的”的神经元不再进行前向传播并且不参与反向传播。因此每次输入时，神经网络会采样一个不同的架构，但所有架构共享权重。这个技术减少了复杂的神经元互适应，因为一个神经元不能依赖特定的其它神经元的存在。因此，神经元被强迫学习更鲁棒的特征，它在与许多不同的其它神经元的随机子集结合时是有用的。

我们在前两个全连接层使用失活。如果没有失活，我们的网络表现出大量的过拟合。 失活大致上使要求收敛的迭代次数翻了一倍。

1.3 学习细节

我们使用随机梯度下降来训练我们的模型，样本的batch size为128，动量为0.9，权重衰减为0.0005。权重衰减不仅仅是一个正则项：它减少了模型的训练误差。权重w的更新规则是：
在这里插入图片描述

1.4 小结

如果出错，欢迎批评指正！

方法	作用
ReLU	提高速度
GPUS	提高速度
局部相应归一化	减小过拟合，泛化能力提高
重叠池化	减小过拟合，泛化能力提高
丢弃法	减小过拟合，泛化能力提高
权重衰减	减小过拟合，泛化能力提高

2 网络框架

2.1 Feature map 维度计算

简单的来说，在cnn的每个卷积层,数据都是以三维形式存在的。可以把它看成许多个二维矩阵叠在一起，其中每一层称为一个feature map。

在这里插入图片描述

2.2 网络结构分析

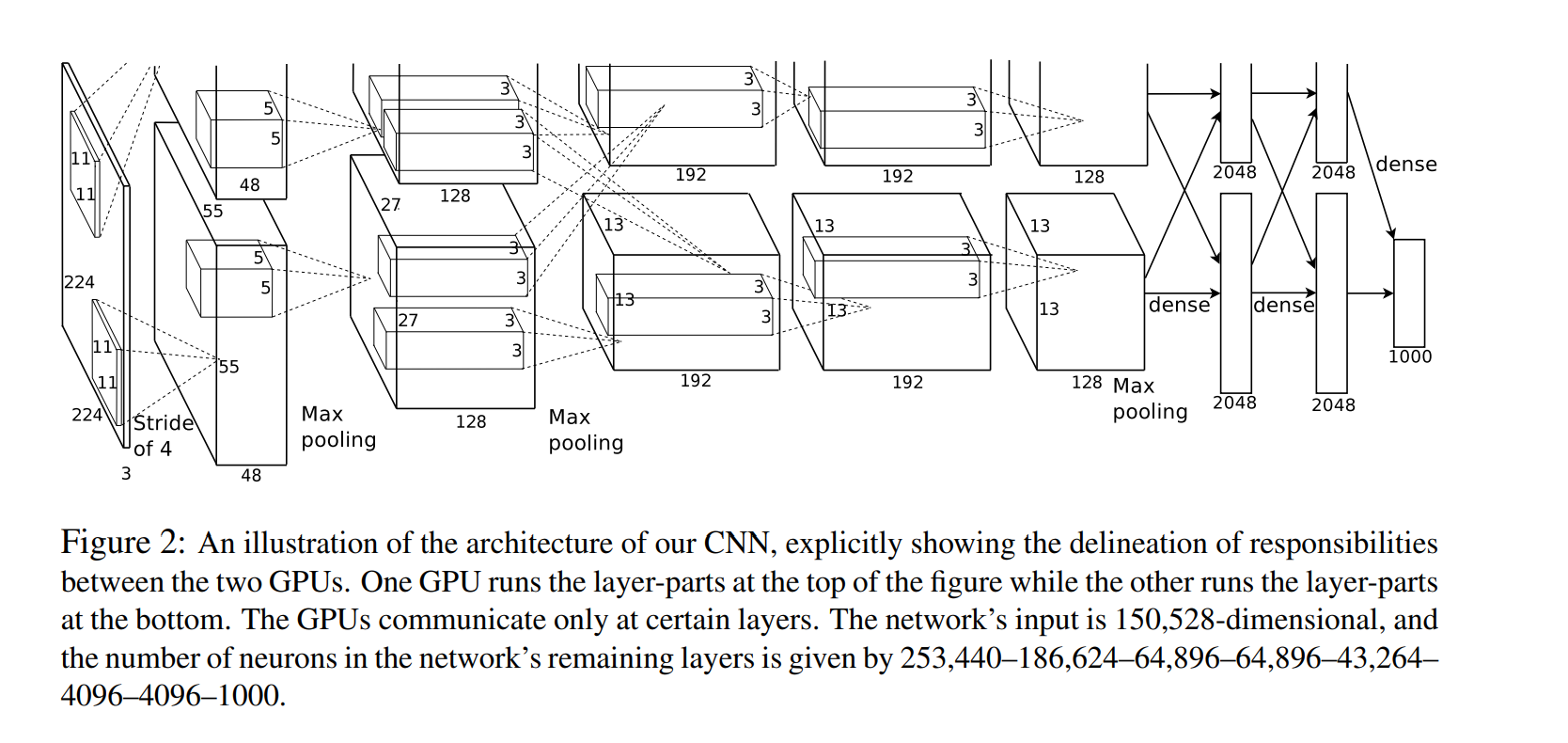
在这里插入图片描述

As a fun aside, if you read the actual paper it claims that the input images were 224×224, which is surely incorrect because (224 – 11)/4 + 1 is quite clearly not an integer. This has confused many people in the history of ConvNets and little is known about what happened. My own best guess is that Alex used zero-padding of 3 extra pixels that he does not mention in the paper.
from CS231n blog

根据上面的计算公式，我们来对各层feature map尺寸进行梳理：

值得注意的是：由于本人的电脑只有一块GPU，所以所有的卷积都是在一块GPU上实现的。

我看了很多的神经网络的设计，目前我也不太知道谁说的是正确的，所以下面的内容和代码部分仅供参考。同时，我也会多给几种网络模型供大家学习参考。

卷积层1得到的feature map: (227 - 11 + 2 × 0) ÷ 4 + 1 = 55
重叠池化层得到的feature map：(55 - 3) ÷ 2 + 1 = 27
卷积层2得到的feature map: (27 - 5 + 2 × 2) ÷ 1 + 1 = 27
重叠池化层得到的feature map：(27 - 3) ÷ 2 + 1 = 13
卷积层3得到的feature map: (13 - 3 + 2 × 1) ÷ 1 + 1 = 13
卷积层4得到的feature map: (13 - 3 + 2 × 1) ÷ 1 + 1 = 13
卷积层5得到的feature map: (13 - 3 + 2 × 1) ÷ 1 + 1 = 13
重叠池化层得到的feature map：(13 - 3) ÷ 2 + 1 = 6
Flatten展开：6 × 6 × 128 × 2 = 9216
全连接层1：9216 -> 4096
丢弃层：p = 0.5
全连接层2：4096 -> 4096
丢弃层：p = 0.5
全连接层3：4096 -> 1000

3 神经元数量和参数数量

3.1 计算方法

神经元的数量 = feature map大小(高宽) * feature map数量(维度)
卷积层的参数 = 卷积核大小 x 卷积核的数量+ 偏置数量(即卷积的核数量)
全连接层的参数数量 = 上一层节点数量(pooling之后的) x 下一层节点数量 + 偏置数量（即下一层的节点数量）

参考阅读：AlexNet中的参数数量 侵权删！

接下来梳理一下各层的参数情况：

输入层：图片大小：宽高通道(RGB)依次为W * H * C = 224 x 224 x 3, 即150528像素。
第1个隐层, 卷积层，使用96个 11 x 11 x 3的卷积核，节点数量为： 55(W) x 55(H) x 48(C ) x 2 = 290400。本层参数数量为: (11 * 11 * 3 * 96) + 96 = 34848

注意，这里是上下两块GPU计算，单个GPU是48，两个在一起计算就是96个卷积核。在某个卷积层中，可以有多个卷积核：下一层需要多少个feature map，本层就需要多少个卷积核。

第2个隐层, 卷积层，使用256个 5 x 5 x 48的卷积核，节点数量为： 27(W) x 27(H) x 128(C ) x 2 = 186624。本层参数数量为: (5 * 5 * 48 * 128+128) * 2 = 307456。最后"*2"是因为网络层均匀分布在两个GPU上，先计算单个GPU上的参数，再乘以GPU数量2。即5 * 5 * 48 * 256 + 256 = 307456。
第3个隐层, 卷积层，使用384个 3 x 3 x 192的卷积核，节点数量为： 13(W) x 13(H) x 192(C ) x 2 = 64896。本层参数数量为: 3 * 3* 256 * 384 + 384 = 885120。
第4个隐层, 卷积层，使用384个 3 x 3 x 128的卷积核，节点数量为： 13(W) x 13(H) x 192(C ) x 2 = 64896。本层参数数量为: 3 * 3* 192 * 384 + 384 = 663936。
第5个隐层, 卷积层，使用256个 3 x 3 x 192的卷积核，节点数量为： 13(W) x 13(H) x 128(C ) x 2 = 43264。本层参数数量为: 3 * 3* 192 * 256 + 256 = 442624。
第6个隐层，全连接层，节点数量为： 4096。参数数量为：(6 * 6 * 128 * 2) * 4096 + 4096 = 37752832，

所谓6，就是在经历最大池化后，矩阵由13 * 13转化为了6 *6。（13 - 3）/ 2 + 1 = 6

第7个隐层，全连接层，节点数量为： 4096。参数数量为： 4096 * 4096 + 4096 = 16781312。
第8个隐层，全连接层，也是1000-way的softmax输出层，节点数量为： 1000。参数数量为： 4096 * 1000 + 1000 = 4097000。

可以看到这个参数数量远远大于之前所有卷积层的参数数量之和。也就是说AlexNet的参数大部分位于后面的全连接层。

3.2 小结

总结： 对于隐层节点和参数的计算，可以简单的理解为：孤立的看待某一隐层，找到对应的输入和输出层。节点数等于输出的feature map的尺寸（包括高宽和通道数），参数数量为输入层的卷积核大小×卷积核数量+卷积核数量或上一层节点数量(pooling之后的) x 下一层节点数量 + 偏置数量（即下一层的节点数量）。
如果对这部分不理解的可以私信我，或QQ1257663033。

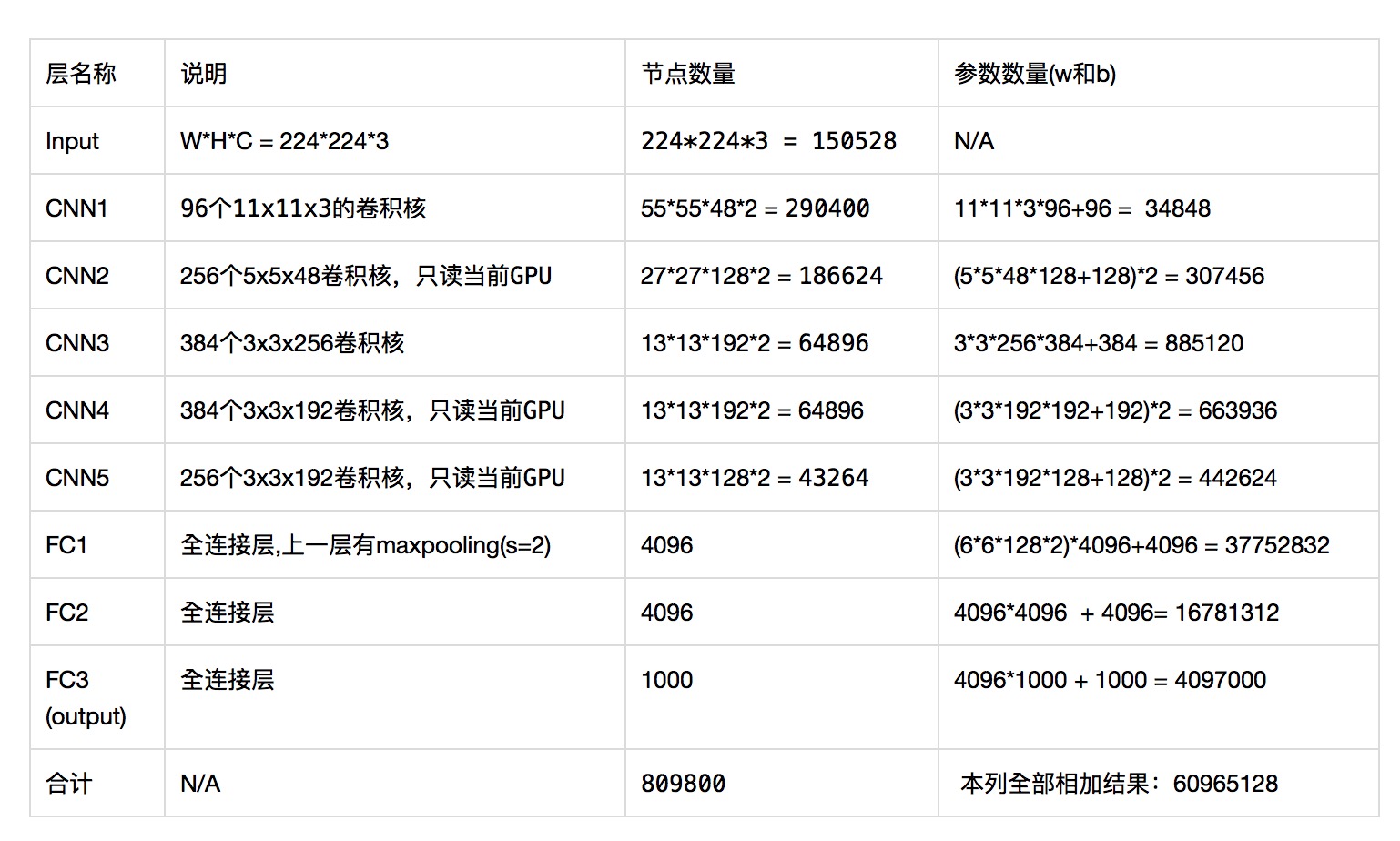
最后，为了方便查看，汇总为表格如下，其中最后一行给出了AlexNet的参数总量。

请添加图片描述

4 网络搭建

4.1 基本架构

基本结构的搭建可参见该博客

使用pytorch搭建AlexNet并训练花分类数据集
这些博客和视频的博主开源了自己的代码，下面是修改的网络层，因为我设置的输入是227 * 227，所以对池化和填充的大小做了改变。并且在后面也给出了两种解释最终的效果图。发现差别并不大。

net：

import torch
from torch import nn
import torch.nn.functional as F


class MyAlexNet(nn.Module):
    def __init__(self):
        super(MyAlexNet, self).__init__()

        self.c1 = nn.Conv2d(in_channels=3, out_channels=96, kernel_size=11, stride=4, padding=0)
        self.ReLU = nn.ReLU()
        self.s1 = nn.MaxPool2d(kernel_size=3, stride=2)

        self.c2 = nn.Conv2d(in_channels=96, out_channels=256, kernel_size=5, stride=1, padding=2)
        self.s2 = nn.MaxPool2d(kernel_size=3, stride=2)

        self.c3 = nn.Conv2d(in_channels=256, out_channels=384, kernel_size=3, stride=1, padding=1)
        self.c4 = nn.Conv2d(in_channels=384, out_channels=384, kernel_size=3, stride=1, padding=1)
        self.c5 = nn.Conv2d(in_channels=384, out_channels=256, kernel_size=3, stride=1, padding=1)

        self.s5 = nn.MaxPool2d(kernel_size=3, stride=2)
        self.flatten = nn.Flatten()

        self.f6 = nn.Linear(9216, 4096)  # 256 * 6 * 6 = 9216
        self.f7 = nn.Linear(4096, 4096)
        self.f8 = nn.Linear(4096, 1000)

        self.f9 = nn.Linear(1000, 10)

    def forward(self, x):
        x = self.ReLU(self.c1(x))
        x = self.s1(x)
        x = self.ReLU(self.c2(x))
        x = self.s2(x)
        x = self.ReLU(self.c3(x))
        x = self.ReLU(self.c4(x))
        x = self.ReLU(self.c5(x))
        x = self.s5(x)
        x = self.flatten(x)
        x = self.f6(x)
        x = F.dropout(x, p=0.5)
        x = self.f7(x)
        x = F.dropout(x, p=0.5)
        x = self.f8(x)
        x = F.dropout(x, p=0.5)
        x = self.f9(x)
        x = F.dropout(x, p=0.5)
        return x


if __name__ == "__main__":
    x = torch.rand([1, 3, 227, 227])
    model = MyAlexNet()
    print(model)
    y = model(x)

4.2 API架构

测试的是fashion_mnist数据集。
net：

import torch
from torch import nn

MyAlexNet = nn.Sequential(
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=0),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),

    nn.Conv2d(96, 256, kernel_size=5, stride=1, padding=2),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),

    nn.Conv2d(256, 384, kernel_size=3, stride=1, padding=1),
    nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, stride=1, padding=1),
    nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, stride=1, padding=1),
    nn.ReLU(),

    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),

    nn.Linear(9216, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 1000),
    nn.Dropout(p=0.5),
    nn.Linear(1000, 10))

X = torch.randn(1, 1, 227, 227)
for layer in MyAlexNet:
    X = layer(X)
    print(layer.__class__.__name__, 'Output shape:\t', X.shape)

train_d2l：

import torch
from d2l import torch as d2l
from NetAPI import MyAlexNet
import matplotlib.pyplot as plt


batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=227)

lr, num_epochs = 0.01, 10
d2l.train_ch6(MyAlexNet, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
plt.show()

测试结果：
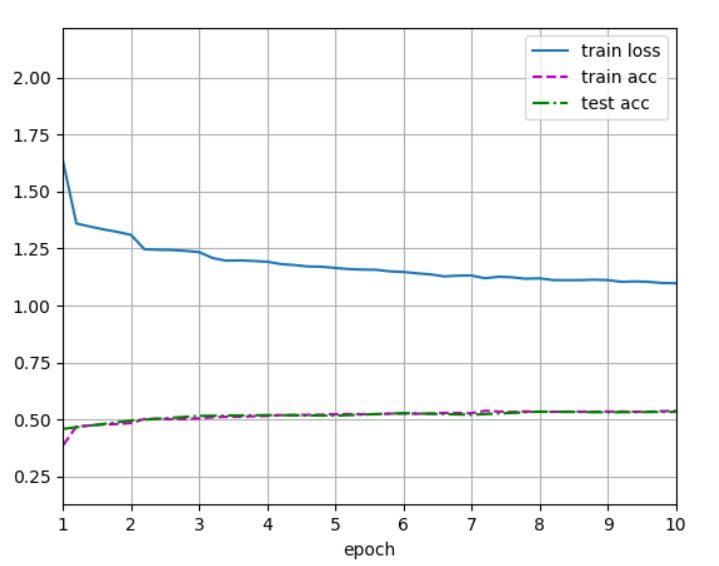
在这里插入图片描述

本人还测试了输入图像为224 * 224的网络：

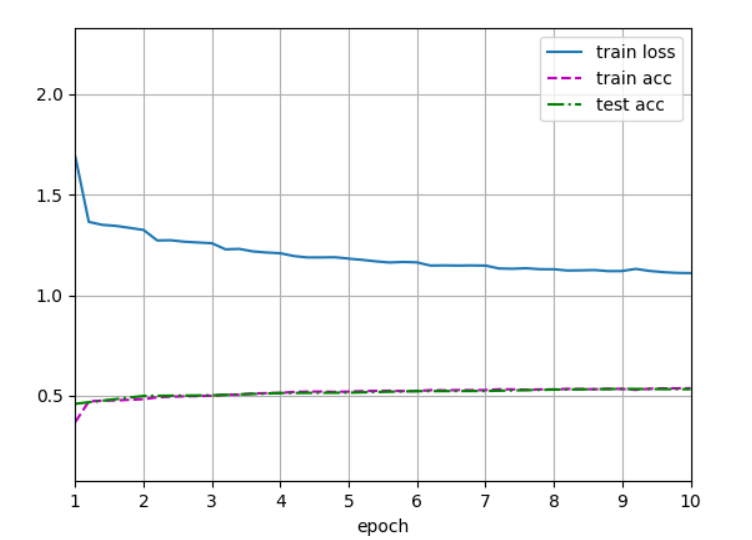
在这里插入图片描述
可以看到两者的训练出来的网络，精度相差不大，所以也没有必要去纠结输入图像到底是224 * 224还是227 * 227咯。

4.3 Pytroch官方架构

from torchvision.models.alexnet import alexnet

class AlexNet(nn.Module):

    def __init__(self, num_classes: int = 1000) -> None:
        super(AlexNet, self).__init__()
        self.features = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Conv2d(64, 192, kernel_size=5, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Conv2d(192, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(384, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(256, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
        )
        self.avgpool = nn.AdaptiveAvgPool2d((6, 6))
        self.classifier = nn.Sequential(
            nn.Dropout(),
            nn.Linear(256 * 6 * 6, 4096),
            nn.ReLU(inplace=True),
            nn.Dropout(),
            nn.Linear(4096, 4096),
            nn.ReLU(inplace=True),
            nn.Linear(4096, num_classes),
        )

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        x = self.features(x)
        x = self.avgpool(x)
        x = torch.flatten(x, 1)
        x = self.classifier(x)
        return x