目录:
一.统计与时间序列分析基础
1.基本概念
- 总体,个体,样本
? ? ? ? ? ? ? ? 总体: 总体是人们研究对象的全体。(关键词:全体,全部)
? ? ? ? ? ? ? ? 个体: 总体中的每一个基本单位称为个体,个体的特征用一个变量 (如 x ) 来表示。
? ? ? ? ? ? ? ? 样本: 从总体中随机产生的若干个个体的集合称为样本。
- 频数,平均值,中位数,标准差,方差,极差
? ? ? ? ? ? ? ? 频数:?将数据的取值范围划分为若干个区间,然后统计这组数据在每个区间中出现的次数, 称为频数。
? ? ? ? ? ? ? ? 平均值(E(x)):总体求和后再除以总体的个数。??

? ? ? ? ? ? ? ? 中位数:中位数是将数据由小到大排序后位于中间位置的那个数值。
? ? ? ? ? ? ? ? 标准差(δ,s):各个数据与均值偏离程度的度量。计算公式(至与为什么是1/(n - 1),在介绍完基本概念会进行详细解释):
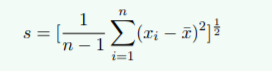
? ? ? ? ? ? ? ? ?方 差(D(x),Var(x)): 标准差的平方。
? ? ? ? ? ? ? ? ?极 差(R):最大值与最小值的差。
- ?中心距,偏度,峰度
? ? ? ? ? ? ? ? ?r阶中心距:? E(x-E(x))^r
? ? ? ? ? ? ? ? 均值:一阶中心距。
? ? ? ? ? ? ? ? 方差:二阶中心距。
? ? ? ? ? ? ? ? 偏度 : 三阶中心距,反应分布的对称性,ν1 >0 称为右偏态,此时数据位于均值右边的比位于 左边的多;ν1 <0 称为左偏态,情况相反; 而 ν1 接近 0 则可认为分布是对称的。
? ? ? ? ? ? ? ??峰度:四阶中心距,是分布形状的另一种度量。

- 自由度:在数学中能够自由取值的变量个数,如有3个变量x、y、z,但x+y+z=18,因此其自由度等于2。?
? ? ? ? ? ? ? ? 现在来解答标准差为什么不是 1/n,而是1/(n-1)。

? ? ? ? 可发现,最终化简结果并不是δ^2,所以需要调整参数使我们的估计为无偏估计。大部分小伙伴还是第一次接触无偏估计,那么什么是无偏估计呢?
请参考:简述无偏估计和有偏估计 - 科学空间|Scientific Spaces
2.几个重要的概率分布
- 正态分布?
? ? ? ? ?正态分布随机变量 X 的密度函数曲线呈中间高两边低、对称的钟形,期望 (均值) EX = μ,方差 DX = σ 2,记作 X ~ N(μ, σ2 ),σ 称均方差或标准差,当 μ = 0, σ = 1 时称为标准正态分布,记作 X ~ N(0, 1)。正态分布完全由均值 和方差 σ 2 决定,它的偏 度为 0,峰度为 3。
- X^2 分布?
? ? ? ? 若 X1, X2, · · · , Xn 为相互独立的、服从标准正态分布 N(0, 1) 的随机变量,则它们 的平方和 Y = Pn i=1 X2 i 服从 χ 2 分布,记作 Y ~ χ 2 (n),n 称自由度,它的期望 EY = n, 方差 DY = 2n。
- t分布

- F分布

?3.正态总体统计量的常用分布

? ? ? ? 设有两个总体 X ~ N(μ1, σ2 ) 和 Y ~ N(μ2, σ2 ),及由容量分别为 n,n 的两个样本 确定的均值 xˉ, yˉ 和标准差 s1, s2,则

4.参数估计。
- 点估计:点估计是用样本统计量确定总体参数的一个数值。评价估计优劣的标准有无偏性、最 小方差性、有效性等,估计的方法有矩法?( 可参考:? ? ?第六章 参数估计-矩估计:通过课后题理解矩估计 - 知乎)、极大似然法等。
????????????????????????????????标准:无偏性、最 小方差性、有效性等
????????????????????????????????方法:矩法、极大似然法等
????????????????????????????????在字母上加 ? 表示估计值
????????????????????????????????缺点:精度,可信度较低
- 区间估计:总体的待估参数记作 θ(如 μ, σ2 ),由样本算出的 θ 的估计量记作 ?θ ,人 们常希望给出一个区间 [ ?θ1, ?θ2],使 θ 以一定的概率落在此区间内。若有
![]()
? ? ? ? 则 [ ?θ1, ?θ2] 称为 θ 的置信区间,?θ1, ?θ2 分别称为置信下限和置信上限,1 ? α 称为置信概率或置信水平,α 称为显著性水平。
? ? ? ?给出的置信水平为 1-α 的置信区间 [ ?θ1, ?θ2],称为 θ 的区间估计。置信区间越小,估 计的精度越高; 置信水?平?越?大,估计的可信程度越高。但是这两个指标显然是矛盾的,通常是在一定的置信水平下使置信区间尽量小。
5.假设检验
? a.单个总体 N(μ, σ^2 ) 均值 μ 的检验
- 双边检验:H0 :μ = μ0,H1 :μ ?= μ0;
- 右边检验:H0 :μ ? μ0,H1 :μ > μ0;
- 左边检验:H0 :μ ? μ0,H1 :μ < μ0;
? b.分布拟合检验(X^2检验法)
? ? ? ?χ ^2 检验就是在总体的分布未知的情况下, 根据样本 X1, X2, · · · , Xn 来检验关于总体分布的假设。
eg:H0:总体 X 的分布函数 为 F(x)? ? ?;? ???H1:总体 X 的分布函数不是 F(x)
????????总体 X 为离散型:H0:总体 X 的分布律为 P{X = t} = p, i = 1, 2, · · ·
????????总体 X 为连续型:H0:总体 X 的概率密度为 f(x).
若 F(x) 的形式已知, 但有参数值未知, 需要先用最大似然估计法估计参数, 然后作检验.
二.手算时间序列
绪论:
? ? ? ? ? ? ? ? ? 时间序列数据本质上反映的是某个或某些随机变量时间不断变化的趋势,而时间序 列? ? ? ? ? ? ? ?方法的核心就是从数据中挖掘出这种规律,并利用其对将来的数据做出估计。
应用方向:
-
?描述过去
-
分析规律
-
预测未来
影响因素:
-
长期变动趋势(T)
-
季节变动趋势(S)
-
周期变动趋势(C)
-
不规则变动(I)
1.简单移动平均法
一组在某一个值附近波动的数据,那么可以用这组数据的平均值来近似拟合下一次可能出现的值。
以过去2期作为预测:
| 期数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 真实值 | 3 | 2 | 3 | 3 | 3 | 1 | 3 |
| 预测值 | 2.5 | 2.5 | 3 | 3 | 2 | ||
| 误差 | 0.5 | 0.5 | 0 | 2 | 1 |
????????????????????????y^3=( y1 + y2 )/2=2.5
????????????????????????…… 以此类推 ……
为了使预测的准确度更高,可以通过标准误差来衡量,标准误差越小越好。
标准误差计算公式:
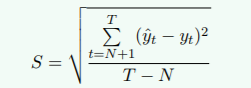
????????????????????????????????????????????????T: 总期数
????????????????????????????????????????????????N: 选定的期数
????????????????????????????????????????????????yt: 实际值
????????????????????????????????????????????????y^t: 预测值
2.加权移动平均法
对于简单移动平均法来说,把各期数据等同看待是不合理的,应考虑各期数据的重要性,因此引入加权移动平均法。
加权平均移动公式:

????????????????????????????????W1,W2,W3………… :权重
????????????????????????????????y1,y2,y3…… ……:实际值
????????????????????????????????Mtw: 预测值
? ? ? ? ? ?对于w的选择:一般是近期的权数大,远期的权数小。
同样的,也可以使用标准误差来衡量合适的预测期数。
3.趋势移动平均法
? ? ? ? 当时间序列出现直线增加或减少的变动趋势时,用简单移动平均法和加权移动平均法来预测会出现滞后偏差,利用移动平均滞后方差的规律来建立直线趋势 的预测模型,就是趋势移动平均法。
定义:一次移动平均法与二次移动平均法:

进行一次移动平均法和二次移动平均法之后,可以使用直线预测模型(如下)

?相关参数详情:
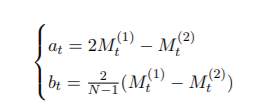
??????????以2期数据为例得到第9期预测模型进行说明
| 期数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 生产量 | a | b | c | d | e | f | g | h | i |
| 一次(A) | (a+b)/2 | (b+c)/2 | (c+d)/2 | (d+e)/2 | …… | …… | (g+h)/2 | ||
| 二次 | (A[3]+A[4])/2 | (A[4]+A[5])/2 | …… | …… | (A[7]+A[8])/2 |
????????????????????????M^(1)9=(g+h)/2
????????????????????????M^(2)9=(A[7]+A[8])/2
????????????????????????a9=2*M^(1)9-M^(2)9
????????????????????????b9=2/(2-1)*(M^(1)9-M^(2)9)
????????????????????????y^ 9+m = a9 + b9 *m
同样的,也可以使用标准误差来衡量合适的预测期数
4.指数平滑法
? ? ? ?移动平均法中一次移动平均加权为0,二次及更高次移动平均数的权数永远保持对称,即两端权数小,中间权数大,而更符合实际的方法是对各期观测 值依时间顺序进行加权平均 作为预测值,因此引入指数平滑法。
-
一次指数平滑法
一次指数平滑公式:

????????????????????????????????????????y1,y2,y3…… …… :时间序列
????????????????????????????????????????α :加权系数(0 < α < 1)
????????????????????????????????????????S t(1):全部历史数据的加权平均
????????预测模型:
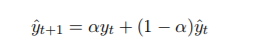
α 的选择:
-
时间序列波动不大, α 可以取小一点,0.1~0.5,以减少修正幅度
-
时间序列又明显的变动倾向, α 应取大一点,0.6~0.8,使预测模型灵敏度高一些。
S0 的选择:
-
数据较多时(大于 20),可选用第一期数据为初始值
-
数据较小时(小于 20),一般选用最初几期实际值的平均值
同样的,也可以使用标准误差来衡量合适的预测期数
-
二次指数平滑法
? ? ? ?当时间序列的变动出现直线趋势时,用一次指数平滑法进行预测,存在明显的滞后偏差。因此引入二次指数平滑法
????????二次指数平滑公式:
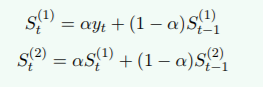
St? ?(1)? ?:? ?一次指数的平滑值
St (2): 二次指数的平滑值
可以使用直线趋势模型预测:![]() m=1,2,3……
m=1,2,3……
参数计算公式:
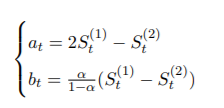
-
三次指数平滑法
若时间序列的变动表现为二次曲线趋势时,则需要用三次指数平滑法
三次指数平滑值计算公式:
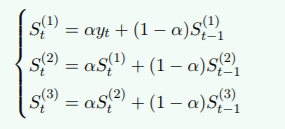
?预测模型: ![]()
![]()
?参数计算公式:

三.?常用时间序列模型
1.差分指数平滑法
? ? ? ?为了从数据变换的角度去应对可能出现的滞后偏差,在运用指数平滑法以前先对数据作一些技术上的处理(差分),使之能适合于 一次指数平滑模型,以后再对输出结果作技术上的返回处理,使之恢复为原变量
的形态。
一阶差分指数平滑模型 具体公式:
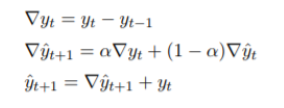
? ? ?使用一阶差分预测 t==9 时的使用量
| t | 使用量 | 差分 | 差分指数平滑值(α=0.4) | 预测值 |
|---|---|---|---|---|
| 1 | 8 | |||
| 2 | 10 | 2 | ||
| 3 | 11 | 1 | 2 | 12 |
| 4 | 13 | 2 | 1.6(1x0.4+2x0.6) | 12.6 |
| 5 | 14 | 1 | 1.76(2x0.4+1.6x0.6) | 14.76 |
| 6 | 17 | 3 | 1.5(1x0.4+1.76x0.6) | 15.5 |
| 7 | 20 | 3 | 2.1(3x0.4+1.5x0.6) | 19.1 |
| 8 | 24 | 4 | 2.46(3x0.4+2.1x0.6) | 22.46 |
| 9 | ??? | ??? | 4x0.4+2.46x0.6==3.1 | 27.1 |
? ? 当时间序列呈现二次曲线增长时,可用二阶差分指数平滑模型来预测,具体公式:

优点:
-
克服一次指数平滑法的滞后偏差
-
对初始值的问题有显著的改进
2.自适应滤波法
? ? ? ? 先用一组给定的权数来 计算一个预测值,然后计算预测误差,再根据预测误差调整权数以减少误差。这样反复 进行,直至找出一组“最佳”权数,使误差减少到最低限度。这样的方法叫做自适应滤波法。
预测公式:

参数说明:? ? ? ? ? ? ?^y_t+1 :t+1期的预测值
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? w_i: 第t_i+1期的权数
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? y_t-i+1:第t-i+1期的观测值
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? N:权数的个数
权数调整公式:
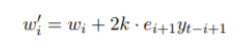
参数说明:? ? ? ? ? ? ? ? ?w‘_i:调整后的权数
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?w_i:调整前的常数
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?k:学习常数
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?e_i+1: 第i+1期的预测误差
? ? ? ?在每一次调整后,把现有的权数作为初始权数,再次反复执行,直到预测误差没有明显改进时才停止。
权数的确定:
N:一般取周期(以一年为周期:N=12;已季节为周期:N=4),如果没有明显周期,可用自相关系数法(自相关系数 - 搜狗百科)确定。·
k: 一般为 1/N
初始权数(w):如无其他依据,一般取 1/N
优点: a.?可根据预测意图来选择权数 的个数和学习常数,以控制预测。
? ? ? ? ? ? b. 它使用了全部历史数 据来寻求最佳权系数。
3.趋势外推预测方法
根据事物的历史和现时资料,寻求事物发展规律,从而推测出事物未 来状况
主要包括六个阶段:
????????????????a.选择应预测的参数
????????????????b.收集必要的数据
????????????????c. 利用数据拟合曲线
????????????????d.趋势外推
????????????????e.预测说明
????????????????f.研究预测结果在进行决策中应用的可能性。
典型数学模型:
????????????????1.指数曲线
????????????????2.修正指数曲线
????????????????3.生长曲线
????????????????4.包络曲线
-
指数曲线法
数学模型:

? ????????????????????????????????????????????????????????A,K用最小二乘法求得
-
修正指数曲线法
? ? ? ? ? ? ?当呈现指数饱和时,为了防止出现指数爆炸的情况,使用修正指数曲线法。?
? ? ? ? ? ? ?增长率增长趋势 :初期迅速,随后逐渐降低。
预测模型:
![]()
参数确定:
K:
????????????????可确定时:采用最小二乘法确定a,b
????????????????不可确定时:采用三合法进行确定。
三合法:即把时间序列的n个观察值等分为三部分,每部分有 m 期,即 n = 3m 。
????????????????S1: y_1,y_2,y_3, …… …… y_m;
????????????????S2: y_m+1,y_m+2,…… …… y_2m;
????????????????S3: y_2m+1,y_2m+2, …… …… y_3m

使用以上步骤,可以确定a,b值。
4.Logistic 曲线 (生长曲线)
? ? ? 生长曲线,即包括发芽,生长,成熟的过程,在这三个阶段,生长速度是不同的,往往呈现为 生长缓慢 ---》突然加快---》又减慢,呈 ’ S ‘ 形
数学模型:
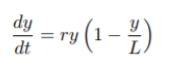
参数说明:
????????????????y:预测值
????????????????L:y的极限值
????????????????r:增长率常数
解上数学模型微分方程有:
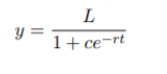
?故记Logistic曲线的一般形式:

什么时候能使用logistics曲线方法?
————看给定数据倒数的逐期增长量的比率是否接近某 一常数 b
即:
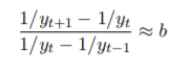
?参数确定:
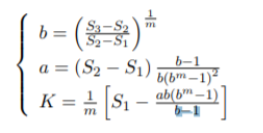
5.平稳时间序列
? ? ?平稳:均值,方差,协方差没有系统的变化,且严格消除周期性变化
引入函数基本概念:
- 均值函数:
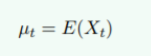
- ?方差函数:
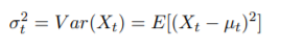
- ?协方差函数:

- ?自相关函数:
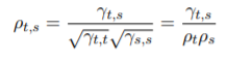
样本的秩:原来样本数据在顺序统计量中的排位数
????????????????eg: 样本数据: 1,5,-1,0,-9????????????????????????
????????????????????????顺序统计量: -9,-1,0,1,5
????????????????????????可知,秩统计量:5,3,4,1,2
平稳系列:随机系列满足 均值函数为常数 且 协方差 与 t 无关。
平稳白噪声系列:

如何判断一列数据是否是白噪声序列?
? ? ?(把握白噪声没有前后相关性,使用Daniel检验,而Daniel检验时建立在Spearman相关函数的基础上,接下来将一 一介绍)
? ? ? ?对于二维总体 (X, Y ) 的样本观测数据 (x1, y1),(x2, y2), · · · ,(xn, yn),可得各分量 X, Y 的一元
样本数据 x1, x2, · · · , xn 与 y1, y2, · · · , yn 。设 x1, x2, · · · , xn 的秩统计量是 R1, R2, · · · , Rn
;y1, y2, · · · , yn 的秩统计量是 S1, S2, · · · , Sn 。当 X, Y 联系比较紧密时,这两组秩统计量联系
也是紧密的。Spearman 相关系数定义为 这两组秩统计量的相关系数,即 Spearman 相关系数是

做双边检验:
![]()
自相关系数为0时:说明此随机序列为平稳序列。

t分布表:t-分布临界值表 - 豆丁网
6.平稳序列自协方差函数与自相关函数的估计
γ_k的两种估计:
无偏估计:

?有偏估计:

使用 自协方差 估计自相关函数:
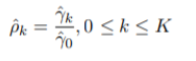
?四.ARMA 时间序列模型与预测
?好戏终于要上场了!
自回归滑动平均模型(Autoregressive moving average model),由自回归模型(AR)与移动平均模型(MA)混合构成。
1.时间序列分析流程
可以根据以下几个问题进行分析:
????????????????????????a.分析的数据是否有价值?是否为白噪声序列?
????????????????????????b.分析的时间序列是否为平稳时间序列?如果不是平稳时间序列该怎么办?
????????????????????????c.当前的观测值受到之前几期数据的影响?分别受到 AR、MA 模型的几期影响?
????????????????????????d.如何检验时间序列模型的好坏?
-
是否是白噪声?是否是平稳时间序列?
a.根据白噪声的特点进行分析:
????????????????????????白噪声序列通常有三个特点:
????????????????????????????????????????1.均值为 0;
????????????????????????????????????????2.方差存在且为常数;
????????????????????????????????????????3.数据前后不相关.
b.根据平稳时间序列进行区别白噪声序列:
????????????????????????平稳时间序列通常有三个特点:
????????????????????????????????????????1. 均值为固定常数
????????????????????????????????????????2. 方差存在且为常数
????????????????????????????????????????3. 协方差只与时间间隔有关(协方差即为自变量 x 与因变量 y 的协同? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?性)
c.如果不是非平稳时间序列? -------可以通过差分变换进行差分处理。
-
当前观测值受之前几期数据的影响?
引入概念:
AC(Autocorrelation Coefficient 自相关系数):用来描述数据自身不同时期的相关程度,即度量历史数据对现在产生的影响。
PAC(Partical Autocorrelation Coefficient 偏自相关系数):同自相关系数大同小异,在计算相关性时移除了中间变量的间接影响。
ACF(Autocorrelation Function 自相关函数):自相关系数构成的序列。
PACF(Partial Autocorrelation Function偏自相关函数):偏自相关系数构成的序列。
-
比较ACF,PACF图判断。

| ACF | PACF | 选用模型 |
|---|---|---|
| 截尾 | 拖尾 | MA |
| 拖尾 | 截尾 | AR |
| 拖尾 | 拖尾 | ARMA |
如何判断截尾与拖尾?
-
拖 尾:
-
数据受到前面 n 期数据影响的效果逐渐递减
-
相关系数不能在某一步之后为0(截尾),而是按指数衰减(或成正弦波形式)
-
-
截 尾:
-
数据受前面 n 期影响出现断崖式下跌
-
相关系数在某一步之后为0
-
平稳性检验:
? ? ? ? 平稳序列通常具有短期相关性,对于平稳的时间序列,自相关系数往往会迅速退化到零(滞后期越短,相关性越高,滞后期为0时,相关性为1);而对于非平稳的数据,退化会发生得更慢,或存在先减后增或者周期性的波动等变动。


2.ARMA 时间序列
-
AR(p)序列

-
MA(q) 序列

- ?ARMA(p, q) 序列
设 {Xt , t = 0, ±1, ±2, · · · } 是零均值平稳序列,满足下列模型:

εt: 零均值、方差是 σ 2 ε 的平稳白噪声,
Xt: 阶数为 p, q 的自回归滑动平均序 列
当 q = 0 时,它是 AR(p) 序列; 当 p = 0 时,它为 MA(q) 序列。
引用 φ(B), θ(B),可以将模型改成:
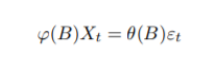
-
φ(B) 和 θ(B) 无公共因子,又 φp ?= 0, θq ?= 0
-
φ(B) = 0 的根全在单位圆外,这一条件称为模型的平稳性条件;
-
θ(B) = 0 的根全在单位圆外,这一条件称为模型的可逆性条件。
平稳性,可逆性可参考博客(arma模型平稳性和可逆性的条件_【时间序列】自回归模型_自说自话的总裁的博客-CSDN博客)
3.ARMA 序列的相关特性(偏相关系数)
由于对本部分内容理解不是十分深刻,希望路过的大佬们可以在评论区推荐好的文章或者在评论区指正交流。了解后,会在下一篇博客中体现出来
-
MA(q) 序列的自相关函数

-
AR(p) 序列的自相关函数

-
ARMA(p, q) 序列的自相关函数

? ????????????????????????????????????????Toeplitz矩阵可参考(Toeplitz矩阵 - 豆丁网)
由于初次学习时间序列,理解不是很深入,希望大家多多指正。
之后深入理解后,会在接下来的博客中展现出来。