系列文章目录
PyTorch Week 3——nn.MaxPool2d、nn.AvgPool2d、nn.Linear、激活层
PyTorch Week 3——卷积
PyTorch Week 3——nn.Module的容器:Sequential、ModuleList、ModuleDice
PyTorch Week 3——模型创建
PyTorch Week 2——Dataloader与Dataset
PyTorch Week 1
PyTorch Week 3——权值初始化操作
前言
本节通过代码和公式推导理解梯度消失和梯度爆炸产生的原理,以及通过初始化权重的解决方法。
一、梯度消失与梯度爆炸
1、通过公式推导分析导致梯度消失和爆炸的原因
不考虑激活函数和偏差,探究权重初始化对输出的影响
演示前一层输出导致梯度爆炸
以3层线性层为例:

假设我们要求取W2的梯度:

可以看出W2的梯度收到前一层输入H1的影响,若H1趋近于0,W2的梯度消失,若H1趋近于无穷大,则W2的梯度爆炸
代码演示
构建了一个100层,每层256个单元的模型,每层的权重采用标准正态分布初始化,mean=0,std=1,输入同样采用normal: mean=0, std=1
class MLP(nn.Module):
def __init__(self, neural_num, layers):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])#列表推导式构建ModuleList模型
self.neural_num = neural_num
def forward(self, x):
for (i, linear) in enumerate(self.linears):
x = linear(x)
return x
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.normal_(m.weight.data)#标准正态分布初始化,mean=0,std=1
layer_nums = 100
neural_nums = 256
batch_size = 16
net = MLP(neural_nums, layer_nums)#构建了一个100层,每层256个单元的模型
net.initialize() #
inputs = torch.randn((batch_size, neural_nums)) # normal: mean=0, std=1
output = net(inputs)
print(output)
打印输出,爆炸了。

下面通过标准差来衡量每层输出数据的分布范围,找一下哪一层的输出开始爆炸
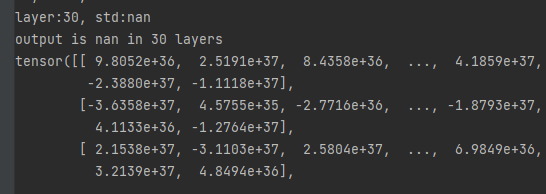
公式推导探究每一层的输出越来越大的原因
不考虑bias,已知X*Y的标准差 = X,Y的标准差的乘积,则第11层的输出H11的方差=n×(X的方差)×(W)的方差,初始化时输入和每一层的权重都是均值0,标准差为1(方差为1)的,所以:第1层第一个单元的输出的标准差为根号下n,每层扩大根号下n倍

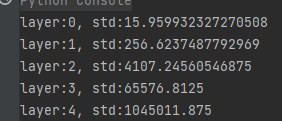
当第一层的个数为256时,标准差大约为16,第二层扩大16倍,标准差为256,以此类推,代码验证与预计表现一致
公式推导探究缓解梯度爆炸的方法
如下图,只要保证每一层的输出方差为1即可


那么为了保证输出的方差等于1,只要让权重的标准差=根号下(1/n)即可。
代码验证
nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))#

可以看出每层的输出依然维持在较小的范围。
二、考虑激活函数的影响
1.Xavier初始化
公式
参考文献:《Understanding the difficulty of training deep feedforward neural networks》
目的:方差一致性,即保持数据尺度(每一层的网络输出值)维持在恰当范围,通常方差为1
针对的激活函数:饱和函数,如Sigmoid,Tanh
为了满足方差一致性,权重的方差应该满足左式。
而权重一般满足均匀分布,为了保证均值为0,均匀分布的上下限互为相反数,设上限为a,则权重的方差应满足三分之a方,令其等于左式,则求得权重初始化应满足右式。

代码
首先添加激活函数层,然后修改权重初始化方式
def forward(self, x):
for (i, linear) in enumerate(self.linears):
x = linear(x)
x = torch.tanh(x)#添加tanh层
print("layer:{}, std:{}".format(i, x.std()))
if torch.isnan(x.std()):
print("output is nan in {} layers".format(i))
break
return x
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
a = np.sqrt(6 / (self.neural_num + self.neural_num))#计算均匀分布a
tanh_gain = nn.init.calculate_gain('tanh')#利用nn.init.calculate_gain获取每一层的a增益
a *= tanh_gain#计算每一层的a
nn.init.uniform_(m.weight.data, -a, a)#权重初始化
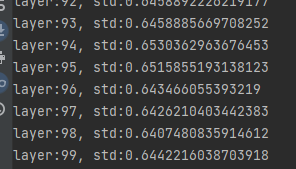
依然维持较小的值

Pytorch也提供了nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)方法用于实现相同的功能
tanh_gain = nn.init.calculate_gain('tanh')
nn.init.xavier_uniform_(m.weight.data, gain=tanh_gain)
完全一致
2.Kaiming初始化方法
参考文献Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
公式
方差一致性
针对的函数:ReLU函数及其变种
经过公式推导,权值的方差和标准差应为:

代码
激活函数改为:
x = torch.relu(x)
初始化改为:
nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num))
结果
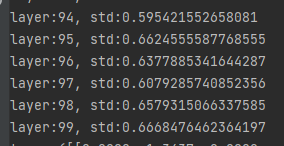
三、十种初始化方法

总结
- 从公式推导的角度,理解梯度消失和梯度爆炸产生的原因是每一层的输出
- 通过推导每一层输出的方差公式分析出:输出层的方差由与神经元的个数,输入的方差和权值的方差有关;权值初始化方差为1能够有效抑制梯度消失和梯度爆炸。
- 针对不同的激活函数,出现了不同的初始化方法,Xavier初始化针对饱和函数,Kaiming初始化针对ReLU及其变种。