一、分组卷积
普通的卷积操作在通道上使’全连接‘的,而分组卷积将输入通道与输出通道都划分为同样的组数,相同组的通道全连接。假设记分组数为g,则计算量与参数量减小到原来的1/g。


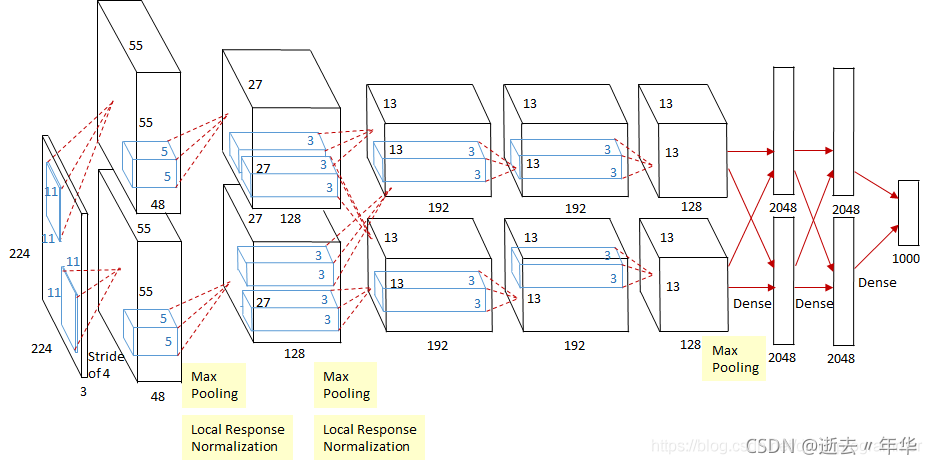
应用场景: 分组卷积最初是在AlexNet网络引入,目的是为了解决单个GPU无法处理含较大计算量和存储需求的卷积层这个问题,采用分组卷积分配到多个GPU上,随着硬件升级,这方面需求减少。目前多使用在移动设备构建小型网络模型。现有GPU加速库(cuDNN)优化有限,效率提升并不如理论显著。
二、转置卷积
转置卷积:又称为‘反卷积’,多用于图像的上采样,改善低分辨率图片。
转置卷积可以看作是普通卷积的一个‘对称‘操作,主要体现在一下两个方面:
- 转置卷积能将普通卷积的输入到输出的尺寸逆反过来。
- 转置卷积的信息正向传播与普通卷积的误差反向传播所用的矩阵相同,反之亦然。
转置卷积讲解带图
三、空洞卷积
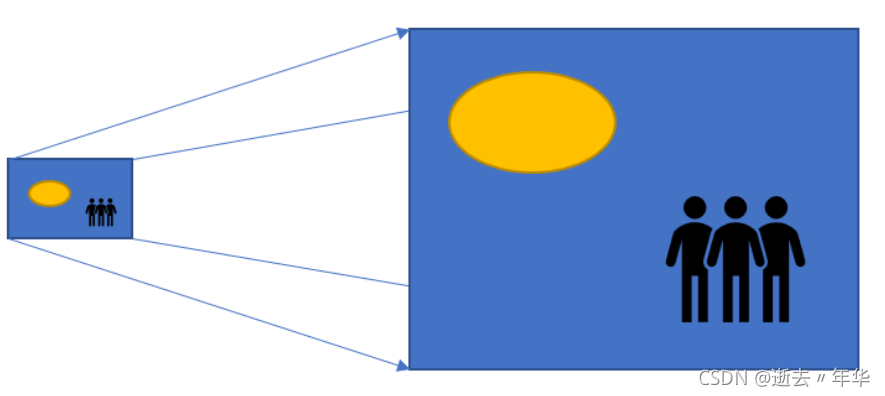
由来:语义分割模型,如全卷积网络,一般采用池化操作来(迅速)扩大特征图的感受野,但同时会丢失特征图的分辨率,丢失一些信息(内部数据结构、空间层级等)导致上采样无法还原一些细节等,从而限制分割精度的提升。如何不采用池化操作就能扩大感受野呢?
空洞卷积:在标准的卷积核中加入’空洞‘,以增加卷积核的感受野。如下图:

空洞卷积细节讲解
四、可变形卷积(ICCV2017)
可变形卷积由来:普通卷积是固定的,规则的,这束缚了感受野的形状,限制了网络对几何形变的适应能力,为了克服困难,在卷积核的每个采样点上添加可学习的偏移量,让采样点不局限于规则的采样点,如图b、c、d。(空洞卷积可视为可变形卷积的特例)

可变形卷积结构图:

可变形卷积的效果:

参考文件:
《百面深度学习》+自我总结+其他博客链接