高斯噪声
高斯噪声是指噪声密度函数服从高斯分布的一类噪声。由于高斯噪声在空间和频域中数学上的易处理性,这种噪声(也称为正态噪声)模型经常被用于实践中。高斯随机变量z的概率密度函数由下式给出:
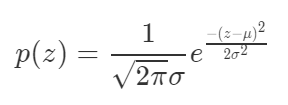
其中z表示灰度值,μ表示z的平均值或期望值,σ表示z的标准差。标准差的平方称为z的方差。高斯函数的曲线如图所示。
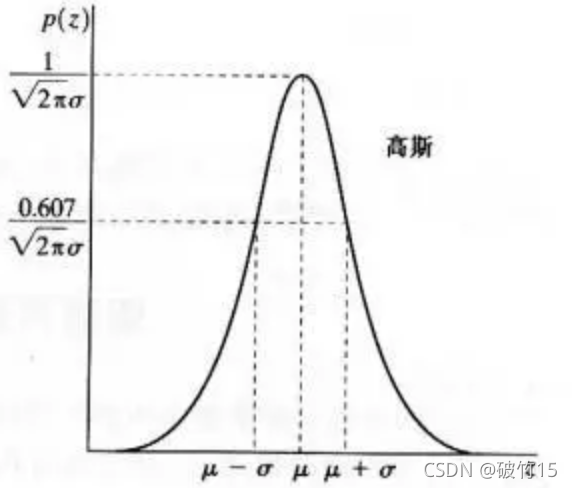
高斯滤波
二维高斯是构建高斯滤波器的基础,其概率分布函数如下所示:
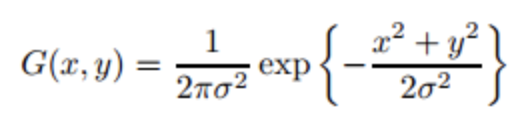
正态分布是一种钟形曲线,越接近中心,取值越大,越远离中心,取值越小。计算平滑结果时,只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值。
高斯平滑在从图像中去除高斯噪声方面非常有效。
高斯平滑的流程:
首先确定权重矩阵
假定中心点的坐标是(0,0),那么距离它最近的8个点的坐标如下:

更远的点以此类推。
为了计算权重矩阵,需要设定σ的值。假定σ=1.5,则模糊半径为1的权重矩阵如下:
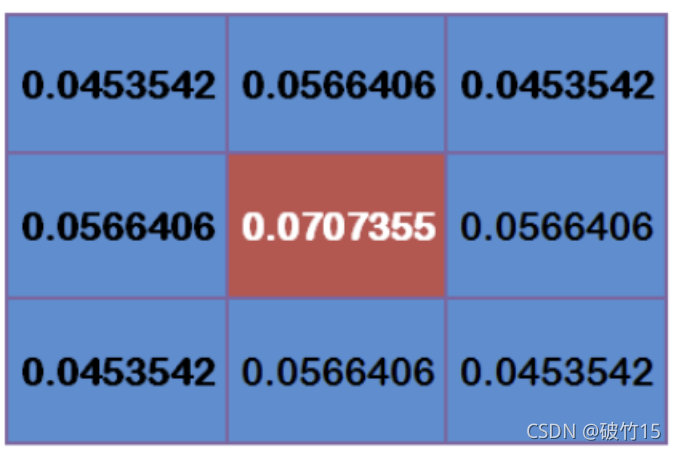
这9个点的权重总和等于0.4787147,如果只计算这9个点的加权平均,还必须让它们的权重之和等于1,因此上面9个值还要分别除以0.4787147,得到最终的权重矩阵。
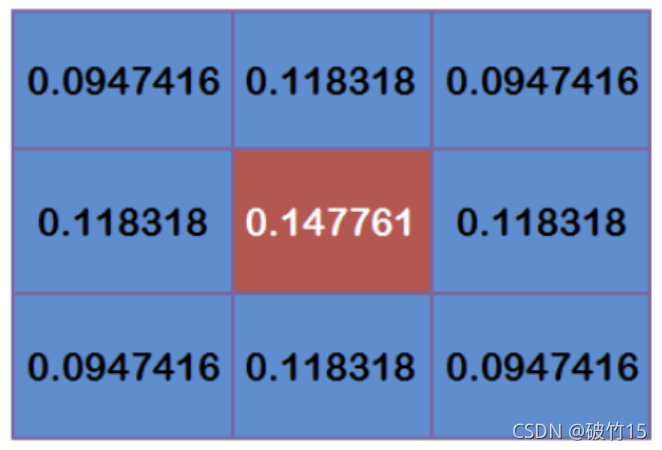
计算高斯模糊
有了权重矩阵,就可以计算高斯模糊的值了。
假设现有9个像素点,灰度值(0-255)如下:
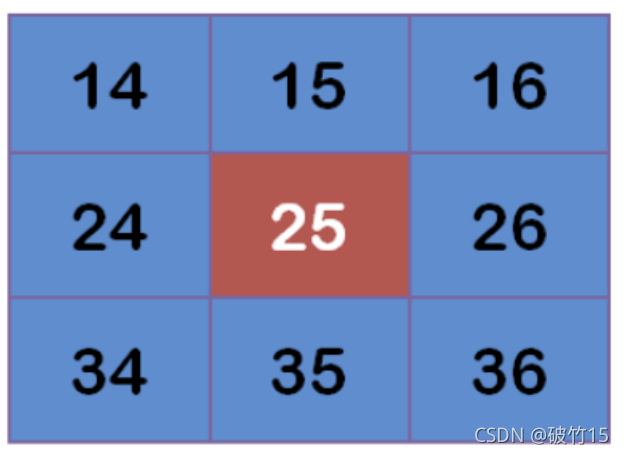
每个点乘以对应的权重值:
??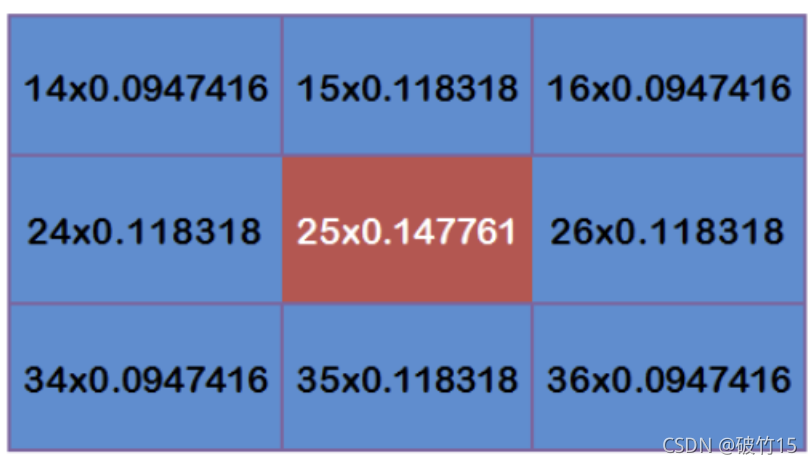
得到
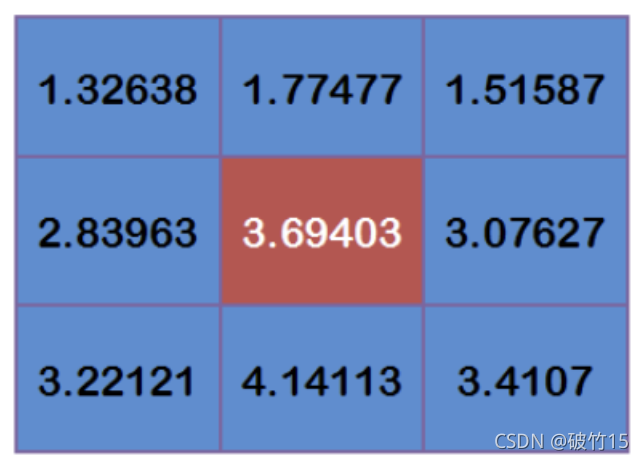
将这9个值加起来,就是中心点的高斯模糊的值。
对所有点重复这个过程,就得到了高斯模糊后的图像。如果原图是彩色图片,可以对RGB三个通道分别做高斯平滑。