[人工智能]Pytorch ---- 梯度下降 学习笔记~~~~~

前两天学的线性模型，穷举权重。今天学梯度下降法求权重。

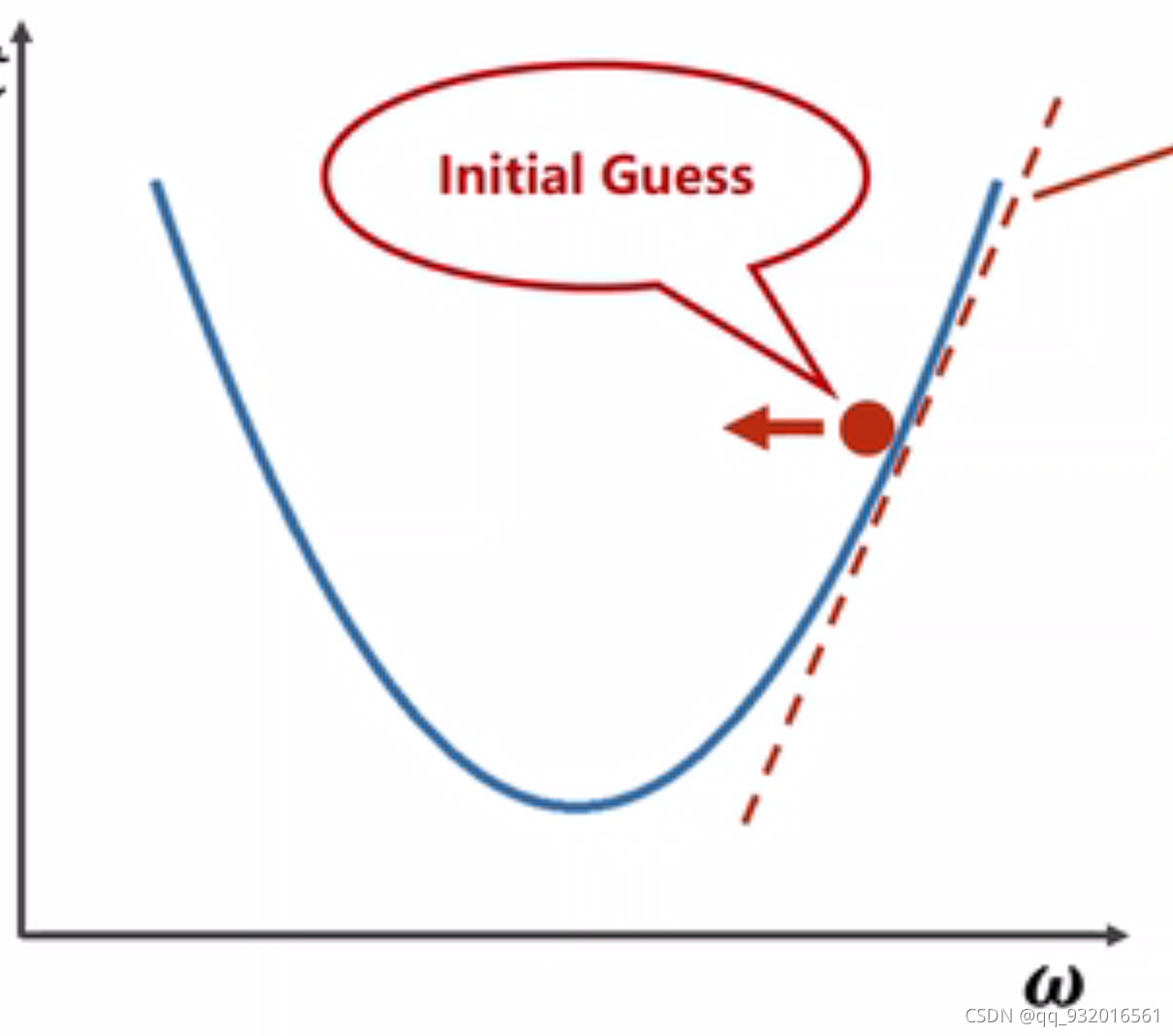
假设所取点为图中红心点。要找到下降的一侧。则求红心点出的导数。按导数定义走。

导数大于0，则X往靠近原点的方向走，
导数小于0，则X往靠近无穷大的方向走。
所以找到导数的负方向。即为下降的方向。

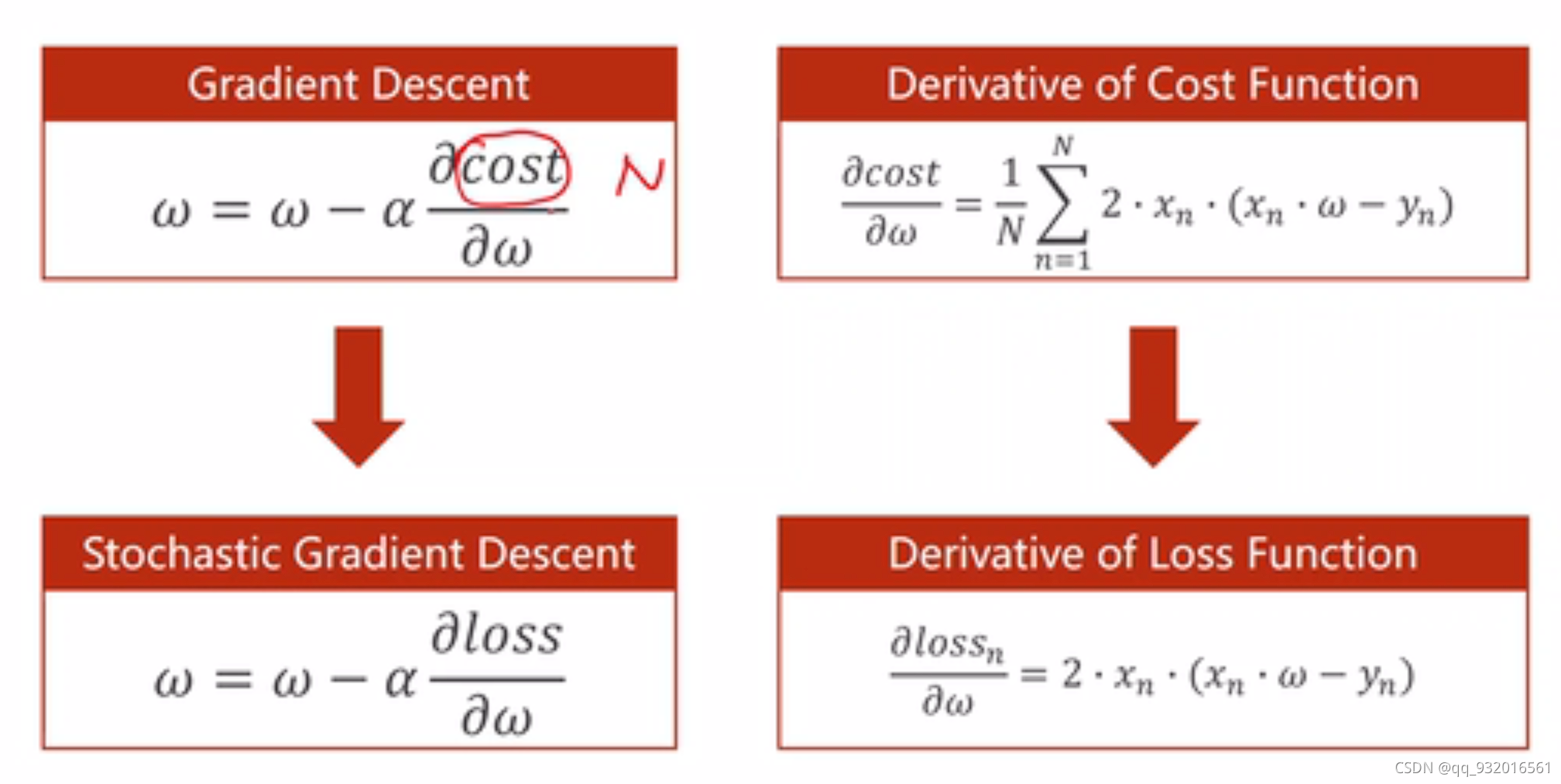
所以在梯度下降算法中，更新权重的方法:
a为学习率 （理解为往前走多少）学习率取的太大容易导致训练失败。

梯度下降算法类似于 贪心算法。找当前情况下的最优步骤。
但也和贪心类似，最后的解未必是全局最优解。
看下图，梯度下降有可能收敛于左边的低估处的局部最优解。但显然，全局最优在右边的低估处。

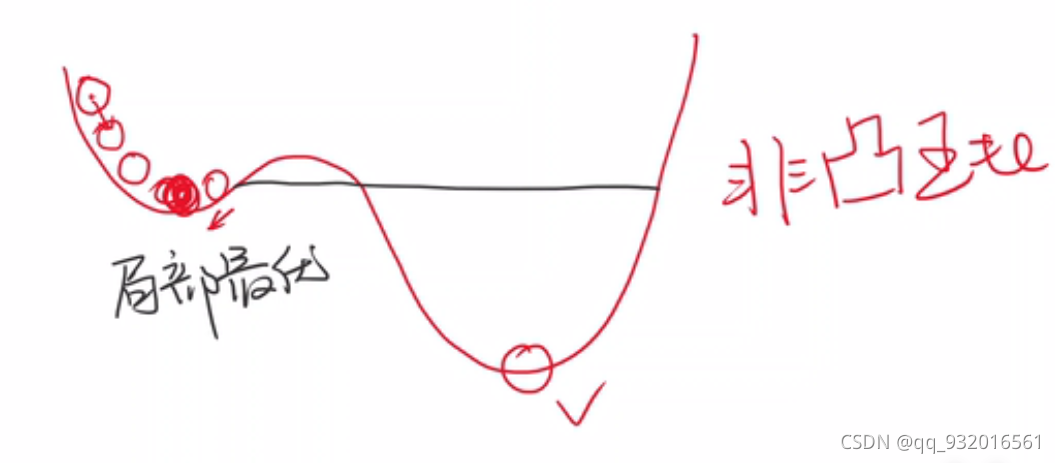
鞍点： 梯度为0的点，就是导数为0的点，即水平线。

将参数全部带入后的公式:

完整代码—梯度下降

import matplotlib.pyplot as plt


# 拿到XY样本数据
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 猜测一个权重W
# 学习率取0.01
a = 0.01


# 计算MSE
def cost(x_data, y_data, w):
    sum_loss = 0
    # 先算当前权重的预测值，然后和真实值Y计算
    for x_val, y_val in zip(x_data, y_data):
        pre_num = x_val * w
        loss = (y_val - pre_num) ** 2
        sum_loss += loss
    return sum_loss / len(x_data)


# 求梯度
def gradient(x_data, y_data, w):
    grad_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        grad_sum += 2 * x_val * (x_val * w - y_val)
    return grad_sum / len(x_data)


if __name__ == '__main__':
    w_ll = []
    mse_ll = []
    w = 1.0
    for i in range(400):  # 循环20次求最优解
        # 先拿mse
        mse = cost(x_data, y_data, w)
        w_ll.append(w)
        mse_ll.append(mse)
        # 拿到梯度
        grad = gradient(x_data,y_data,w)
        # 计算新的权重值
        w -= a * grad
print("权重",w_ll)
print("MSE",mse_ll)

plt.plot(w_ll,mse_ll)
plt.rcParams['font.sans-serif'] = ['KaiTi']
plt.xlabel("权重W")
plt.ylabel("MSE")
plt.show()

可以看到结果:

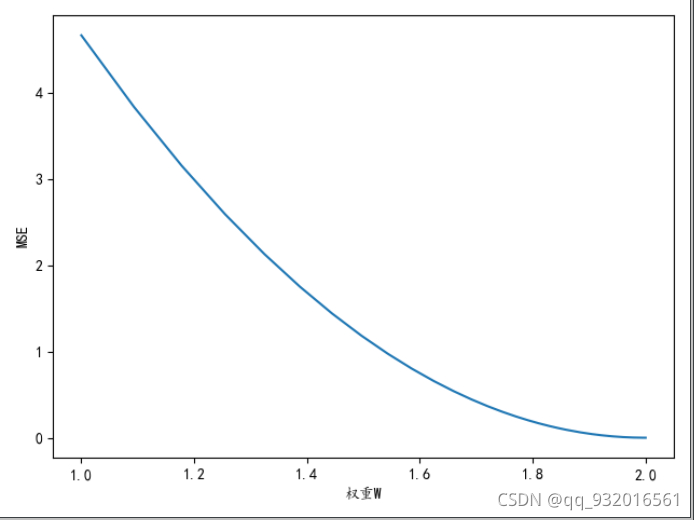
在深度学习里，用的比较多的是随机梯度下降。
在梯度下降里。用整体的均值损失作为梯度依据，在随机的梯度下降里，从整体的均值损失里随机抽一个来使用（或者直接仅计算一个（每一个样本）的损失来使用-代码中这样实现）。
随机梯度下降可能可以解决梯度下降的鞍点问题。

完整代码–随机梯度下降

import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0

# 学习率 a取 0.01
a = 0.01


# 计算单个损失值
def loss(x_val, y_val, w):
    return (w * x_val - y_val) ** 2


# 计算梯度
def gradient(x_val, y_val, w):
    return 2 * x_val * (x_val * w - y_val)


if __name__ == '__main__':
    w_ll = []
    los_ll = []
    for p in range(200):
        for x_val, y_val in zip(x_data, y_data):
            # 计算单个样本的损失值
            losss = loss(x_val, y_val, w)
            w_ll.append(w)
            los_ll.append(losss)
            # 计算梯度
            grad = gradient(x_val, y_val, w)
            # 更新权重
            w -= a * grad
print("权重",w_ll)
print("损失",los_ll)

plt.rcParams['font.sans-serif'] = ['KaiTi']
plt.plot(w_ll, los_ll)
plt.xlabel("权重W")
plt.ylabel("损失")
plt.show()

可以看到结果:

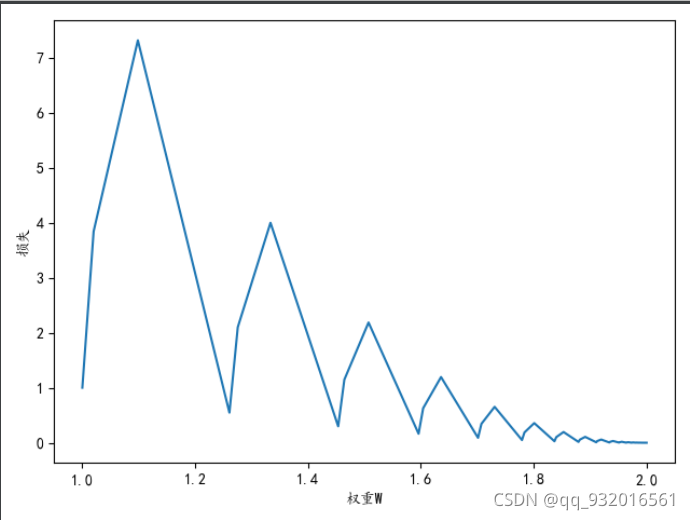
梯度下降在计算梯度的时候是可以并行的。
但随机梯度下降，前后是有依赖关系的，要前一个的权重值。所以无法并行计算。

所以显然，
普通梯度下降，性能差但时间复杂度低。
随机梯度下降，性能高但时间复杂度高。
这里的性能指收敛，求最优解的性能。

在深度学习中，会取一个性能和时间复杂度折中的方案。叫Batch，或 Mini-Batch。
Batch:批量随机梯度下降。将全部数据分为若干个一组，每次求这一组的梯度然后更新。