Task 02 西瓜书第二次打卡(第三章)
3 线性模型
3.1 基本形式
基本形式:
f
(
x
)
=
w
1
x
1
+
w
2
x
2
+
?
+
w
d
x
d
+
b
f(x)=w_1x_1+w_2x_2+\dots+w_dx_d+b
f(x)=w1?x1?+w2?x2?+?+wd?xd?+b即
f
(
x
i
)
=
w
T
x
i
+
b
f(x_i)=w^Tx_i+b
f(xi?)=wTxi?+b
非线性模型:可在线性模型基础上通过引入层级结构或者高维映射得到。
3.2 线性回归
1.定义:线性回归试图学得一个线性模型以尽可能准确地预测实值输出标记
试图学得:
f
(
x
i
)
=
w
x
i
+
b
f(x_i)=wx_i+b
f(xi?)=wxi?+b 使得
f
(
x
i
)
∽
y
i
f(x_i)\backsim y_i
f(xi?)∽yi?
2.确定
w
w
w 和
b
b
b:均方误差最小化(最小二乘法)
3.最小二乘法:试图找到一条直线,使所有样本 到直线上的欧氏距离之和最小
4.最优解
5.多元线性回归:样本有d个属性
3.3 对数几率回归
1.定义:对数几率函数是一种“Sigmoid”函数,单调可微,任意阶可导(是一种分类学习方法)
2.公式:
y
=
1
1
+
e
?
(
w
T
x
+
b
)
y=\frac{1}{1+e^-(w^Tx+b)}
y=1+e?(wTx+b)1?
3.求解 w 和 b方法:极大似然法 引用这位仁兄的解释
3.4线性判别分析 LDA
1.定义:将样例投影到一条直线上,使得同类投影点尽可能相近,异类投影点尽可能远离;对新样本进行分类时,将其投影到一条直线上,根据投影点位置确定新样本的类别。
2.二维示意图:
3.计算方法:同类投影点协方差尽可能小,异类样本投影点的类中心之间距离尽可能大,同时考虑二者
3.5 多分类学习
1.基本思路:拆解法:将多分类任务拆为若干个二分类任务求解。
2.经典的拆分策略:一对一(训练N(N-1)/2个分类器)、一对其余(训练N个分类器)、多对多
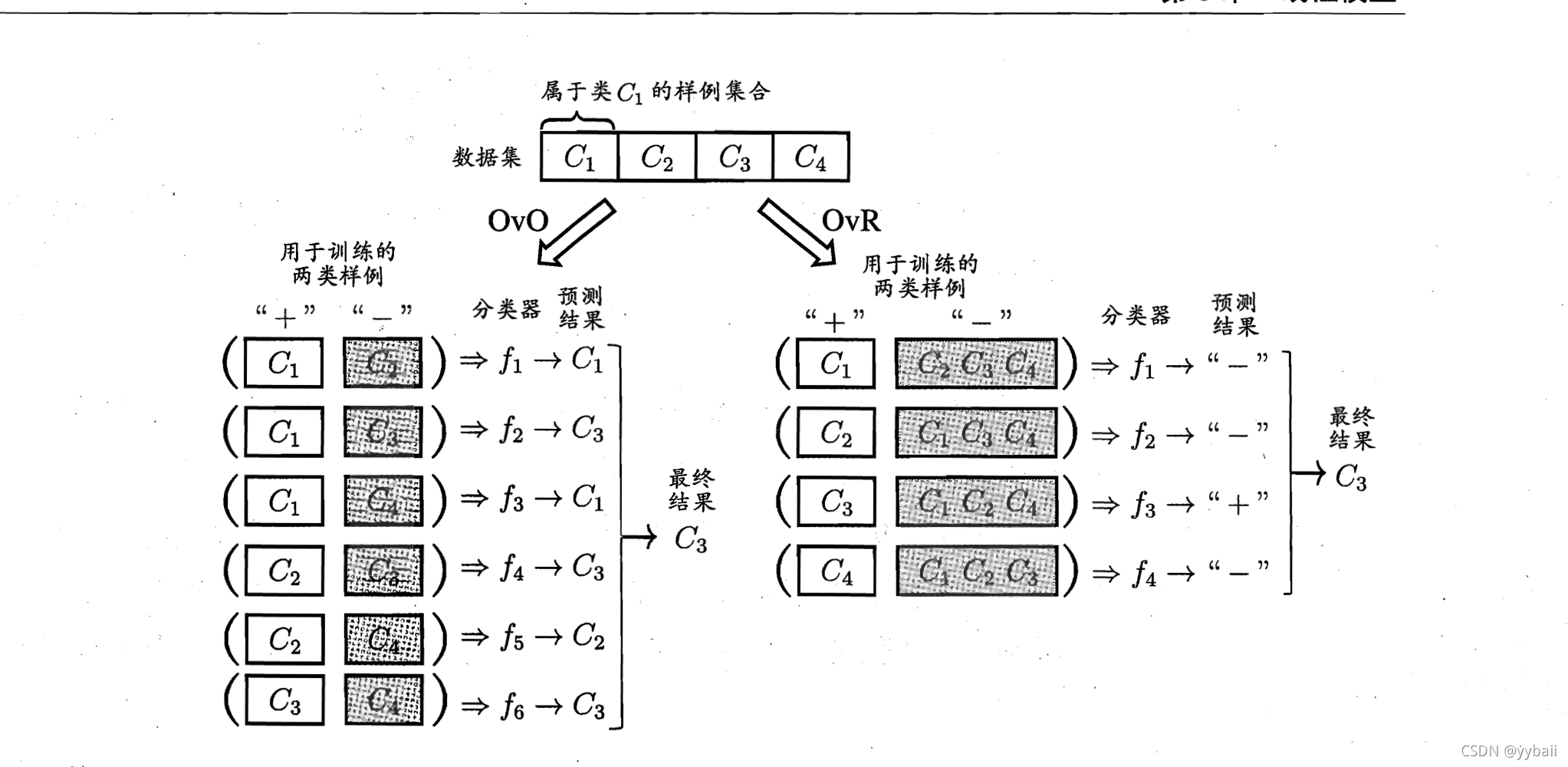
3.MvM常用技术:纠错输出码(ECOC:Error Correcting Output Codes)
ECOC分为两步:
(1)编码:对N个类别做M次划分,每次划分将一部分类别划分为正类,一部分划分为反类,从而形成一个二分类训练集;这样一共产生M个训练集,可以训练出M个分类器。(类别划分通过编码矩阵指定)
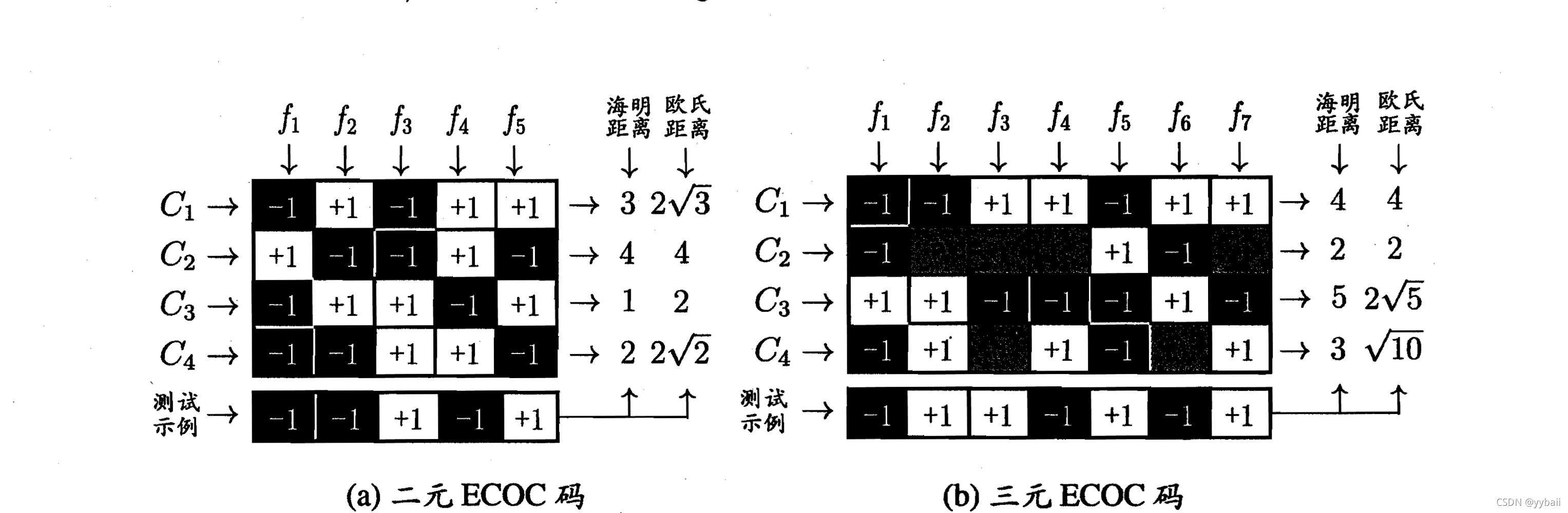
(2)解码:M个分类器分别对测试样本进行预测,这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为最终预测结果。
4.编码矩阵:有二元码(正类、反类)、三元码(正类、反类、停用类)。
3.6 类别不平衡问题
1.定义:指分类任务中不同类别的训练样例数目差别很大的情况
2.基本策略:再缩放(再平衡):代价敏感学习的基础
正常:
y
1
?
y
>
m
+
m
?
\frac{y}{1-y}>\frac{m^+}{m^-}
1?yy?>m?m+? 则预测为正例
调整为:
y
1
1
?
y
1
=
y
1
?
y
?
m
?
m
+
\frac{y^1}{1-y^1}=\frac{y}{1-y}*\frac{m^-}{m^+}
1?y1y1?=1?yy??m+m??(1)
3.三大做法:第一类做法是直接对训练集里的反类样例进行==“欠采样”,即去除一些反例使得正、反例数目接近,然后进行学习;第二类时对训练集里的正类样例进行“过采样”==,及增加一些正例使得正、反列数目接近,再进行学习;第三类则是直接基于原始训练集进行学习,但在用训练好的分类器进行预测时,将公式(1)嵌入到决策过程中,称为“阈值移动”
3.7 阅读材料
1.稀疏表示