[人工智能] MATLAB深入学习S6：数字控制技术—

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> MATLAB深入学习S6：数字控制技术——逐点比较法插补原理 -> 正文阅读

[人工智能]MATLAB深入学习S6：数字控制技术——逐点比较法插补原理

阅读前请注意：

1. MATLAB深入学习是在MATLAB学习笔记的基础上的深度学习，学习这一部分内容需要有较夯实的MATLAB基础，不建议在未掌握基础知识的情况下学习本内容。博客内容由 @K2SO4钾撰写、编辑，发布于 @K2SO4钾的个人投稿与华中师范大学HelloWorld程序设计协会CSDN官方账号 @CCNU_HelloWorld 。注意，如需转载需得到作者 @K2SO4钾的同意与授权！

2. 内容中的代码、示例均为作者原创，内容中的引用、参考等非原创内容均会以参考文献的方式在文末标出。

3. 笔记中示例用MATLAB版本为MATLAB R2019a。

4. 请谅解笔记可能会出现的错误，欢迎指正讨论；由于MATLAB更新导致的旧代码无法使用的情况，也欢迎讨论交流。

文章目录

S6.0 MATLAB学习笔记：传送门汇总

S6.0.1 MATLAB学习笔记：传送门汇总

MATLAB学习笔记0：学习须知

MATLAB学习笔记1：MATLAB概述

MATLAB学习笔记2：MATLAB基础知识（上）

MATLAB学习笔记3：MATLAB编程基础（前半）

MATLAB学习笔记3：MATLAB编程基础（后半）

S6.0.2 MATLAB拓展学习：传送门汇总

MATLAB拓展学习T1：匿名函数和内联函数

MATLAB拓展学习T2：程序性能优化技术

MATLAB拓展学习T3：histogram函数详解

MATLAB拓展学习T4：数据导入与查表技术

S6.0.3 MATLAB深入学习：传送门汇总

MATLAB深入学习S1：简单数字滤波技术的MATLAB实现（1）

MATLAB深入学习S2：无限脉冲响应数字滤波器

MATLAB深入学习S3：简单数字滤波技术的MATLAB实现

MATLAB深入学习S4：元胞自动机原理及MATLAB实现

MATLAB深入学习S5：图像处理技术

MATLAB深入学习S6：数字控制技术——逐点比较法插补原理

S6.0.4 MATLAB应用实例：传送门汇总

MATLAB应用实例Y1：Floyd算法

S6.1 逐点比较法——直线插补

由于我们的机械臂、刀具或者绘画笔很多时候是由电机操控的，而电机操控的方向有限（一般来说在二维平面内就是横轴方向和纵轴方向，三维平面内还需要考虑z轴方向。文章仅分析二维平面内的横纵方向），因此对于一些“斜着走”或者是“按弧线运动”的轨迹，电机操控的机械臂、刀具或者绘画笔不能精确地按照轨迹的方式运动。

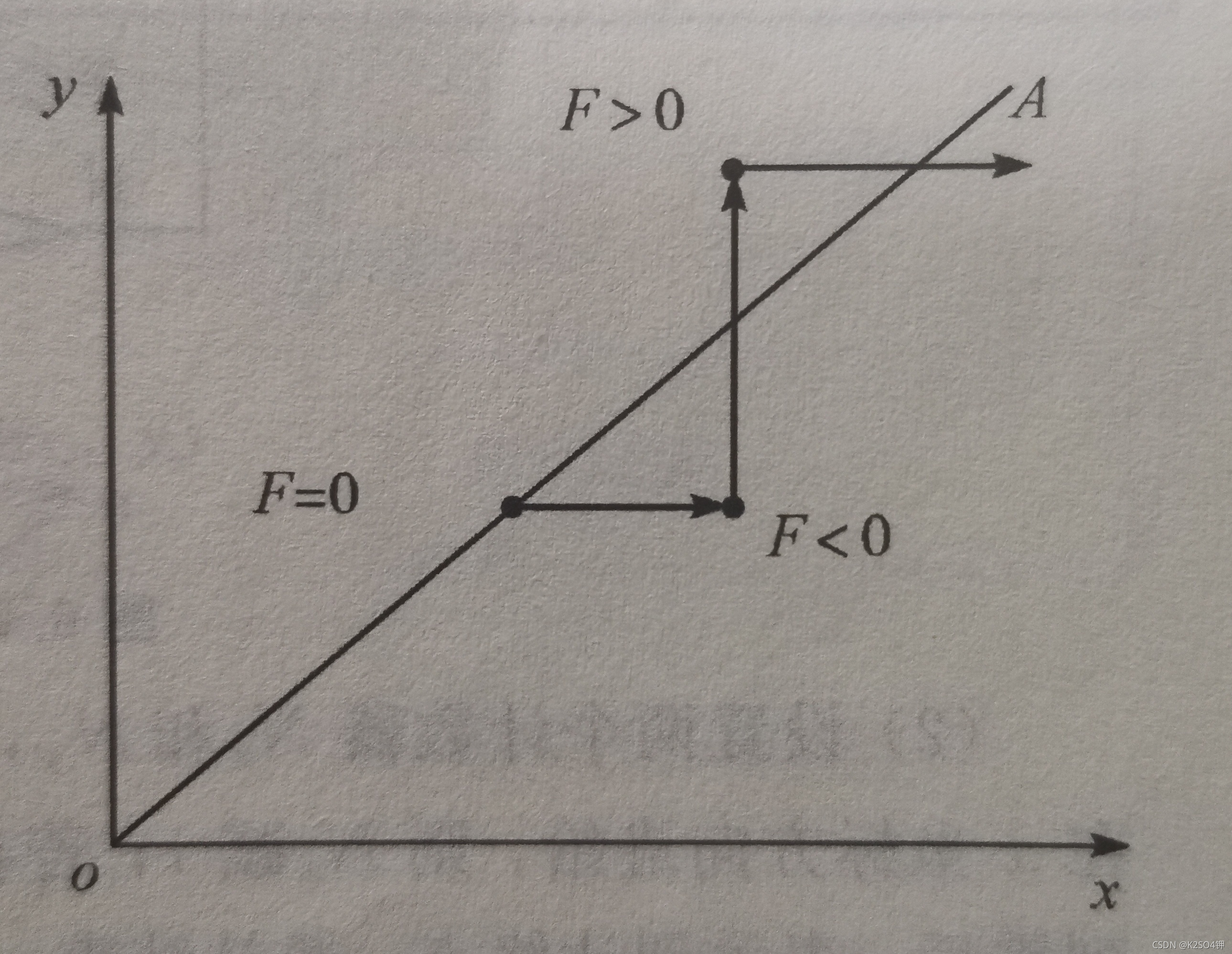
逐点比较法插补其实很好理解，就是把刀具此刻的位置与给定的轨迹（或是理想的轨迹）作比较，看一看目前点是在轨迹的上方还是下方，在轨迹的内侧还是外侧，从而决定下一步到底是横向移动还是纵向移动。不论是横向移动还是纵向移动，都会存在一个“步长”，即移动的最小值，所有的移动距离都是其倍数。当 这个步长很小时，采用逐点比较法进行插补，就可以较精确地对任意方向的直线轨迹进行刀具的移动。

对于曲线，由微积分思想，我们可以 把一条曲线分为若干条直线相连。对每条直线进行上述的方法，再将每条直线刀具预期运行的方式结合到一起，最终就是刀具在整条曲线上的预期移动轨迹了。当然，如果曲线划分为直线“分得太细”，则会导致代码运行时间过长，存储占用过多，代价较大。因此 对于曲线来说，如果精确度要求较高，那么逐点比较法的直线插补是不适用的。

请添加图片描述

大致的原理讲完了，现在来讲一讲细节：

（1）不同象限的直线插补方法稍有差别

与其说是“不同象限的直线”，更准确的说法是从起始点到终点的方向。在确定起点向终点的方向后：

如果方向是第一象限或横轴正方向：

如果目前刀具所在点在轨迹上或者上方，刀具应向右步进；
如果目前刀具所在点在轨迹下方，刀具应向上步进；

如果方向是第二象限或横轴负方向：

如果目前刀具所在点在轨迹上或者上方，刀具应向左步进；
如果目前刀具所在点在轨迹下方，刀具应向上步进；

如果方向是第三象限：

如果目前刀具所在点在轨迹上或者在其下方，刀具应向左步进；
如果目前刀具所在点在轨迹上方，刀具应向下步进；

如果方向是第四象限：

如果目前刀具所在点在轨迹上或者在其下方，刀具应向右步进；
如果目前刀具所在点在轨迹上方，刀具应向下步进；

如果方向是纵轴正方向或负方向

刀具向上或下步进

（2）何时为运行结束

当刀具落在终点坐标范围 $(步进长度) / 2$ 之上或之内，就可以认为刀具移动结束。

（3）以曲线为理想轨迹时

以曲线为理想轨迹时，需要注意将其分割的直线不能过多，否则运行开销太大。其次，将所有直线记录下的刀具移动轨迹进行合成时，要删除两个轨迹中首尾重复的点。

以下为整合的函数和测试的程序。（该函数稍有问题，会在后续的更新中修复。但是原理是正确的）

function [res_x,res_y] = PBPC_Linear_Interpolation(start_x,start_y,current_x,current_y,end_x,end_y,step_x,step_y)
% 
% Take step_x and step_y as the step values in the horizontal and vertical directions, 
% then use the point by point comparison method to return the linear interpolation 
% from point (start_x, start_y) to point (end_x, end_y)
% 
% 以step_x,step_y为横纵方向步进值，逐点比较法返回从点(start_x,start_y)到点(end_x,end_y)的直线插值
% 
% 输入参数(start_x, start_y)：开始点横纵坐标
% 输入参数(end_x, end_y)：结束点横纵坐标
% 输入参数(current_x,current_y)：刀具或绘笔图目前所在的位置
% 输出参数step_x,step_y：刀具或绘笔图的步进值
% 输出参数(res_x,res_y)：刀具或绘笔图的轨迹
%
% 常用调用方式：
% [res_x,res_y] = PBPC_Linear_Interpolation(start_x,start_y,current_x,current_y,end_x,end_y,step_x,step_y)
%
% 编写于2021年10月19日17:26   程序员：K2SO4钾
%

if start_x == end_x
    res_x = [];
    res_y = [];
    res_x(1) = start_x;
    res_y(1) = start_y;
    
    counter = 2;
    if end_y >= start_y
        while(1)
            if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
                    current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
                break
            end
            current_y = current_y+step_y;
            res_x(1,counter) = current_x;
            res_y(1,counter) = current_y;
            counter = counter+1;
        end
    else
        while(1)
            if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
                    current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
                break
            end
            current_y = current_y-step_y;
            res_x(1,counter) = current_x;
            res_y(1,counter) = current_y;
            counter = counter+1;
        end
    end
end        

if start_y == end_y
    res_x = [];
    res_y = [];
    res_x(1) = start_x;
    res_y(1) = start_y;
    
    counter = 2;
    if end_x >= start_x
        while(1)
            if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
                    current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
                break
            end
            current_x = current_x+step_x;
            res_x(1,counter) = current_x;
            res_y(1,counter) = current_y;
            counter = counter+1;
        end
    else
        while(1)
            if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
                    current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
                break
            end
            current_x = current_x-step_x;
            res_x(1,counter) = current_x;
            res_y(1,counter) = current_y;
            counter = counter+1;
        end
    end
end        

if start_x ~= end_x
    k = (start_y-end_y)/(start_x-end_x);
    x0 = start_x;
    y0 = start_y;
    syms x
    func = matlabFunction(k*(x-x0)+y0);

    res_x = [];
    res_y = [];
    res_x(1) = start_x;
    res_y(1) = start_y;

    counter = 2;
    if end_x > start_x && end_y >= start_y
        while(1)
            if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
                    current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
                break
            end
            if current_y >= func(current_x)
                current_x = current_x+step_x;
                res_x(1,counter) = current_x;
                res_y(1,counter) = current_y;
                counter = counter+1;
            else
                current_y = current_y+step_y;
                res_x(1,counter) = current_x;
                res_y(1,counter) = current_y;
                counter = counter+1;
            end
        end
    elseif end_x < start_x && end_y >= start_y
        while(1)
            if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
                    current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
                break
            end
            if current_y >= func(current_x)
                current_x = current_x-step_x;
                res_x(1,counter) = current_x;
                res_y(1,counter) = current_y;
                counter = counter+1;
            else
                current_y = current_y+step_y;
                res_x(1,counter) = current_x;
                res_y(1,counter) = current_y;
                counter = counter+1;
            end
        end
    elseif end_x > start_x && end_y < start_y
        while(1)
            if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
                    current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
                break
            end
            if current_y <= func(current_x)
                current_x = current_x+step_x;
                res_x(1,counter) = current_x;
                res_y(1,counter) = current_y;
                counter = counter+1;
            else
                current_y = current_y-step_y;
                res_x(1,counter) = current_x;
                res_y(1,counter) = current_y;
                counter = counter+1;
            end
        end
    elseif end_x < start_x && end_y < start_y
         while(1)
             if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
                    current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
                break
            end
            if current_y <= func(current_x)
                current_x = current_x-step_x;
                res_x(1,counter) = current_x;
                res_y(1,counter) = current_y;
                counter = counter+1;
            else
                current_y = current_y-step_y;
                res_x(1,counter) = current_x;
                res_y(1,counter) = current_y;
                counter = counter+1;
            end
         end
    end
end

end

%% 仿真
clc,clear all,close all

start_x = 0;
start_y = 3;
end_x = 16;
end_y = 18;
[X,Y] = PBPC_Linear_Interpolation(start_x,start_y,start_x,start_y,end_x,end_y,0.6,0.8);
subplot(121)
plot(X,Y,'linewidth',1.4)
hold on
line([start_x,end_x],[start_y,end_y],'color','r','linewidth',1.4)
title('图像1')

start_x = 0;
start_y = 3;
end_x = 120;
end_y = 140;
[X,Y] = PBPC_Linear_Interpolation(start_x,start_y,start_x,start_y,end_x,end_y,0.1,0.1);
subplot(122)
plot(X,Y,'linewidth',1.4)
hold on
line([start_x,end_x],[start_y,end_y],'color','r','linewidth',1.4)
title('图像2')