多传感器融合定位 第八章 基于滤波的融合方法进阶
参考博客:深蓝学院-多传感器融合定位-第7章作业
 1.环境配置
1.环境配置
1.1 protoc 版本问题
前几章使用的protoc 的版本为3.14, 第七章使用的proto版本为3.15
解决方法:需要安装新版本的proto 3.15x,按照第四章的方式生成对应的文件。
按照GeYao README中的方法,重新生成基于自己基环境protobuf的proto:
打开lidar_localization/config/scan_context文件夹,输入如下命令,生成pb文件
protoc --cpp_out=./ key_frames.proto
protoc --cpp_out=./ ring_keys.proto
protoc --cpp_out=./ scan_contexts.proto
mv key_frames.pb.cc key_frames.pb.cpp
mv ring_keys.pb.cc ring_keys.pb.cpp
mv scan_contexts.pb.cc scan_contexts.pb.cpp
分别修改生成的三个.pb.cpp文件。如下,以ring_keys.pb.cpp为例。
// Generated by the protocol buffer compiler. DO NOT EDIT!
// source: ring_keys.proto
#define INTERNAL_SUPPRESS_PROTOBUF_FIELD_DEPRECATION
#include "ring_keys.pb.h" 替换为 #include "lidar_localization/models/scan_context_manager/ring_keys.pb.h"
#include <algorithm>
之后,用以上步骤生成的的.pb.h文件替换lidar_localization/include/lidar_localization/models/scan_context_manager
中的同名文件。
将.pb.cpp文件替换(注意:需要剪切,确保config文件中新生成的文件都转移到对应目录下,不能重复出现)lidar_localization/src/models/scan_context_manager中的同名文件。
1.2 缺少 fmt 库

git clone https://github.com/fmtlib/fmt
cd fmt/
mkdir build
cd build
cmake ..
make
sudo make install
编译过程中出现:error_state_kalman_filter.cpp:(.text.unlikely+0x84):对‘fmt::v8::detail::assert_fail(char const, int, char const)’未定义的引用**
参考网址: undefined reference to `vtable for fmt::v7::format_error‘
cd catkin_ws/src/lidar_localization/cmake/sophus.cmake
list append 添加 fmt
# sophus.cmake
find_package (Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})
list(APPEND ALL_TARGET_LIBRARIES ${Sophus_LIBRARIES} fmt)
1.3 glog缺少gflag的依赖
logging.cc:(.text+0x6961):对‘google::FlagRegisterer::FlagRegisterer(char const*, char const*, char const*, bool*, bool*)’未定义的引用
#解决办法: 打开glog.cmake , 末尾改为
list(APPEND ALL_TARGET_LIBRARIES ${GLOG_LIBRARIES} libgflags.a libglog.a)
2.增加运模型的 error state kalmam filter
FILE: lidar_localization/src/model/kalman_filter/error_state_kalman_filter.cpp
2.1 融合编码器模型
编码器可以额外提供一个轮速里程计,在不是很高频的编码器情况下,可以做为一个约束边,通过提供线速度(b系) 到上一章节的观测方程中,进行kalman 融合。
注意:
1. 编码器提供的线速度是比较准确的,但是角速度不太准确(转弯存在打滑现象),角速度不宜用作观测边。
2.编码器参与的融合,还有另外一种融合方式,即编码器不当做观测使用,而是和IMU一起进行状态预测,然后再与
其他传感器提供的观测进行滤波融合。具体思路为IMU提供角速度,编码器提供线速度,假设二者频率相同、时间戳已对齐,且外参已标定,那么它们可以直接认为是一个可以通过解算得到姿态、位置的新传感器。

2.2 添加运动约束模型(伪观测)
车子坐标系(前左上),在没有编码器硬件的基础上,可以使用四轮底盘本身的运动属性进行约束,正常情况下,车子只有前向(x)的速度,观测上,y 和 z 向的观测都为0。所以可在观测中添加 Vy 、 Vz 两个约束边。

2.3 代码编写
FILE:catkin_ws/src/lidar_localization/src/models/kalman_filter/error_state_kalman_filter.cpp
2.3.1 调用 CorrectErrorEstimation
case MeasurementType::POSE_VEL:
CorrectErrorEstimationPoseVel(
measurement.T_nb,
measurement.v_b, measurement.w_b,
Y, G, K
);
break;
2.3.2 CorrectErrorEstimationPoseVel 计算 Y ,G ,K
注意:
-
CorrectErrorEstimationPoseVel 函数中输入的v_b 取自 惯导,因为KITTI数据集并没有轮速里程计信息,所以,如果在做融合运动约 束模型时,输入的measurment velocity 为v_b ,可以认为观测是取自ins的。
-
用车子的运动约束(vy = 0;vz = 0)做伪观测约束, 如下所示:
// Eigen::Vector3d v_b_ = {v_b[0], 0, 0}; // measurment velocity (body 系) , 伪观测 (vy 、vz = 0) Eigen::Vector3d v_b_ = v_b; // measurment velocity (body 系) , 融入速度 (vx 取自 惯导)
void ErrorStateKalmanFilter::CorrectErrorEstimationPoseVel( // 计算 Y ,G ,K
const Eigen::Matrix4d &T_nb, const Eigen::Vector3d &v_b, const Eigen::Vector3d &w_b,
Eigen::VectorXd &Y, Eigen::MatrixXd &G, Eigen::MatrixXd &K
) {
//
// TODO: set measurement: 计算观测 delta pos 、 delta ori
//
// Eigen::Vector3d v_b_ = {v_b[0], 0, 0}; // measurment velocity (body 系) , 伪观测 (vy 、vz = 0)
Eigen::Vector3d v_b_ = v_b; // measurment velocity (body 系) , 融入速度 (vx 取自 惯导)
Eigen::Vector3d dp = pose_.block<3, 1>(0, 3) - T_nb.block<3, 1>(0, 3);
Eigen::Matrix3d dR = T_nb.block<3, 3>(0, 0).transpose() * pose_.block<3, 3>(0, 0) ;
Eigen::Vector3d dv = T_nb.block<3, 3>(0, 0).transpose() *vel_ - v_b_ ; // delta v 严格意义上来说,这里的观测是,惯导给的vx
// TODO: set measurement equation:
Eigen::Vector3d dtheta = Sophus::SO3d::vee(dR - Eigen::Matrix3d::Identity() );
YPoseVel_.block<3, 1>(0, 0) = dp; // delta position
YPoseVel_.block<3, 1>(3, 0) = dv; // delta velocity s
YPoseVel_.block<3, 1>(6, 0) = dtheta; // 失准角
Y = YPoseVel_;
// set measurement G
GPoseVel_.setZero();
GPoseVel_.block<3, 3>(0, kIndexErrorPos) = Eigen::Matrix3d::Identity();
GPoseVel_.block<3, 3>(3, kIndexErrorVel) = T_nb.block<3, 3>(0, 0).transpose();
GPoseVel_.block<3, 3>(3, kIndexErrorOri) = Sophus::SO3d::hat( T_nb.block<3, 3>(0, 0).transpose() *vel_ ) ;
GPoseVel_.block<3 ,3>(6, kIndexErrorOri) = Eigen::Matrix3d::Identity();
G = GPoseVel_;
// set measurement C
CPoseVel_.setIdentity();
Eigen::MatrixXd C = CPoseVel_;
// TODO: set Kalman gain:
Eigen::MatrixXd R = RPoseVel_; // 观测噪声
K = P_ * G.transpose() * ( G * P_ * G.transpose( ) + C * RPoseVel_* C.transpose() ).inverse() ;
}
2.3.2 将更新后的vel_b 写到txt 中,进行比较
/*********************write data to txt********************/
#include <list>
#include <sstream>
#include <fstream>
#include <iomanip>
#define DEBUG_PRINT
std::ofstream fused;
std::ofstream fused_vel;
std::ofstream fused_cons;
bool CreateFile(std::ofstream& ofs, std::string file_path) {
ofs.open(file_path, std::ios::out); // 使用std::ios::out 可实现覆盖
if(!ofs)
{
std::cout << "open csv file error " << std::endl;
return false;
}
return true;
}
/* write2txt */
void WriteText(std::ofstream& ofs, Eigen::Vector3d data){
ofs << std::fixed << data[0] << "\t" << data[1] << "\t " << data[2] << "\t" << std::endl;
}
调用
/*init debug print file */
#ifdef DEBUG_PRINT
char fused_path[] = "/home/kaho/shenlan_ws/src/lidar_localization/slam_data/trajectory/fused.txt";
char fused_vel_path[] = "/home/kaho/shenlan_ws/src/lidar_localization/slam_data/trajectory/fused_vel.txt";
char fused_cons_path[] = "/home/kaho/shenlan_ws/src/lidar_localization/slam_data/trajectory/fused_cons.txt";
CreateFile(fused, fused_path );
#endif
------------------------------------------------------------------------------------
/*print vel(body)*/
#ifdef DEBUG_PRINT
Eigen::Vector3d vel_print_ = pose_.block<3, 3>(0, 0).transpose() * vel_; // convert kalman filter velocity to body axis
WriteText(fused, vel_print_ ); // 写进文件夹
#endif
2.4 EVO 评估 及 update后的v_b 比较
evo评估指令
# set up session:
source devel/setup.bash
# save odometry:
rosservice call /save_odometry "{}"
# run evo evaluation:
# a. fused 没有输入运动模型 输出评估结果,并以zip的格式存储:
evo_ape kitti ground_truth.txt fused.txt -r full --plot --plot_mode xy --save_results ./fused.zip
# b. fused_vel 速度观测 输出评估结果,并以zip的格式存储:
evo_ape kitti ground_truth.txt fused.txt -r full --plot --plot_mode xy --save_results ./fused_vel.zip
# c. fused_cons 运动约束伪观测 输出评估结果,并以zip的格式存储:
evo_ape kitti ground_truth.txt fused.txt -r full --plot --plot_mode xy --save_results ./fused_cons.zip
#e. 比较 laser fused 一并比较评估
evo_res *.zip --use_filenames -p
2.4.1 ape 比较
| max | mean | median | min | rmse | sse | std | |
|---|---|---|---|---|---|---|---|
| 无运动约束 | 1.573173 | 0.929147 | 0.927948 | 0.144083 | 0.946438 | 3913.507531 | 0.180083 |
| 速度观测 | 1.580340 | 0.928019 | 0.923693 | 0.130854 | 0.945814 | 3916.404671 | 0.182607 |
| 运动约束 | 1.590144 | 0.928888 | 0.923275 | 0.122330 | 0.946373 | 3918.345359 | 0.181077 |
fused 为无运动约束, fused_vel 为加入惯导速度观测,fused_cons为加入运动约束(伪观测)
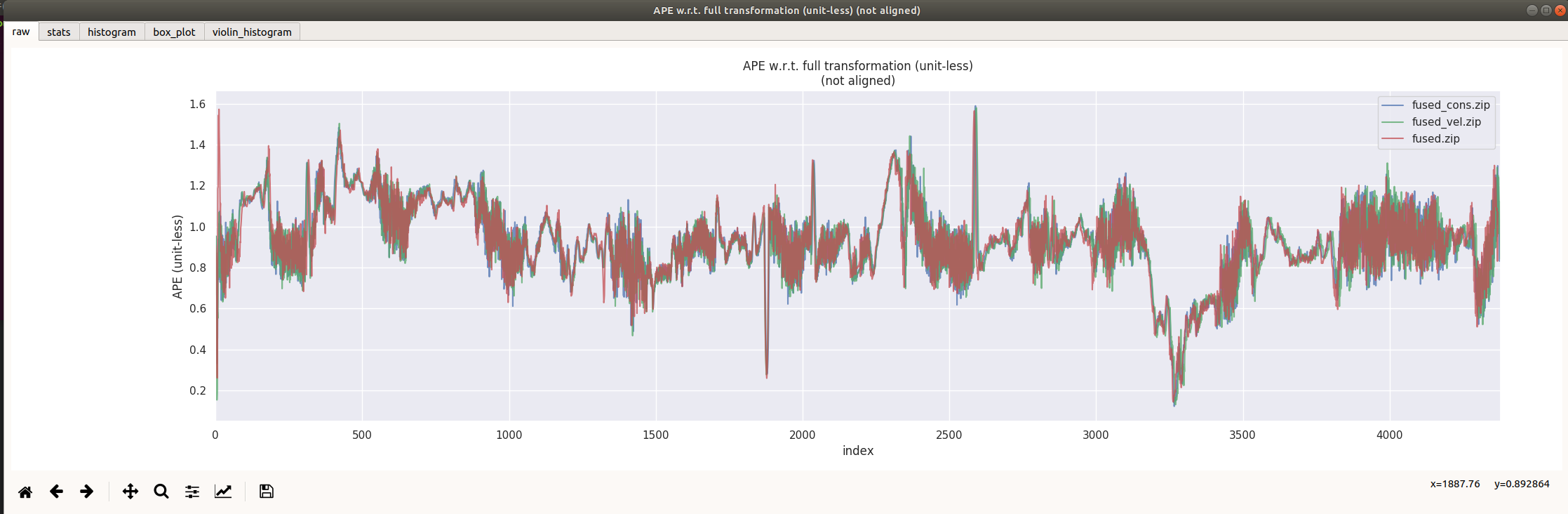
通过观察ape曲线,觉得并无太大差别
| fused 无运动约束 | fused_cons 运动约束 |
|---|---|
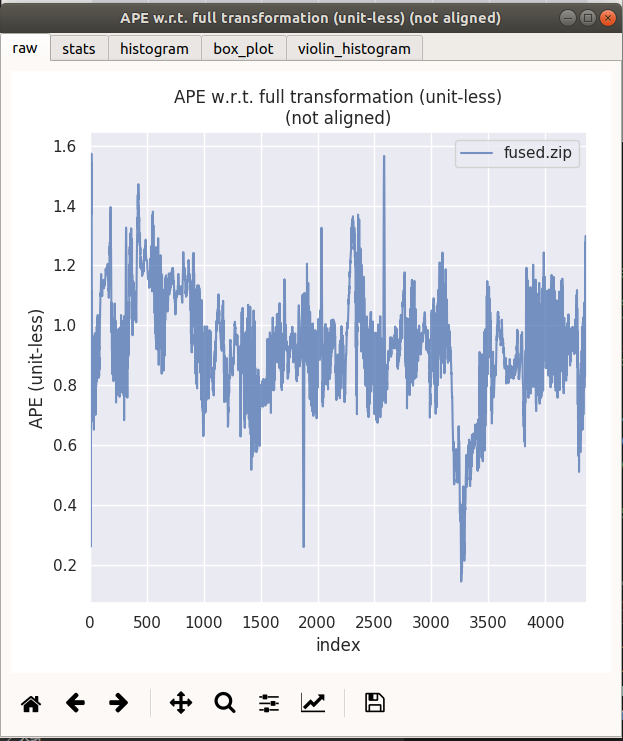 | 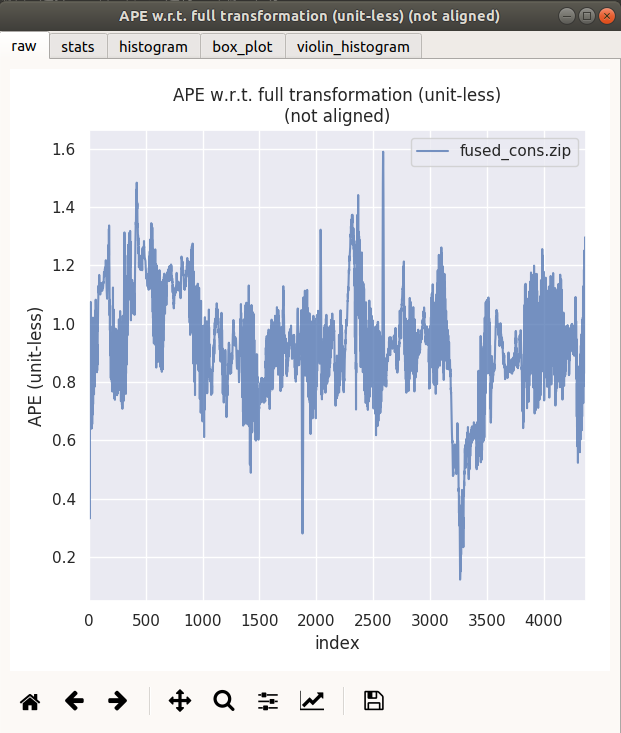 |
2.4.2 使用运动模型后 vel_y vel_z (body系) 比较
fused 为无运动约束, fused_vel 为加入惯导速度观测,fused_cons为加入运动约束(伪观测)
2.4.1 matplotlib 可视化数据
为了方便可视化v_x、v_z ,这里使用matplotlib 可视化数据
FILE: /home/kaho/shenlan_ws/visual/ main.py
# import necessary module
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
fused = np.loadtxt("fused_withoust_cons.txt")
fused_vel_data = np.loadtxt("fused_vel.txt")
fused_cons_data = np.loadtxt("fused_cons.txt")
# x = fused_vel_data[:,0]
y_fused = fused[:,1]
z_fused = fused[:,2]
y_fused_vel = fused_vel_data[:,1]
z_fused_vel = fused_vel_data[:,2]
y_fused_cons_data = fused_cons_data[:,1]
z_fused_cons_data = fused_cons_data[:,2]
plt.plot(y_fused, c='r', label ="y_fused")
plt.plot(y_fused_vel, c='g', label ="Y_fused_vel")
# plt.plot(y_fused_cons_data, c='b', label ="y_fused_cons")
plt.legend();
plt.title('y velocity ',fontsize=18,color='y')
plt.show()
plt.plot(z_fused, c='r', label ="z_fused")
# plt.plot(z_fused_vel, c='g', label ="z_fused_vel")
plt.plot(y_fused_cons_data, c='b', label ="y_fused_cons")
plt.legend();
plt.title('z velocity ',fontsize=18,color='y')
plt.show()
2.4.2 vel_y 比较
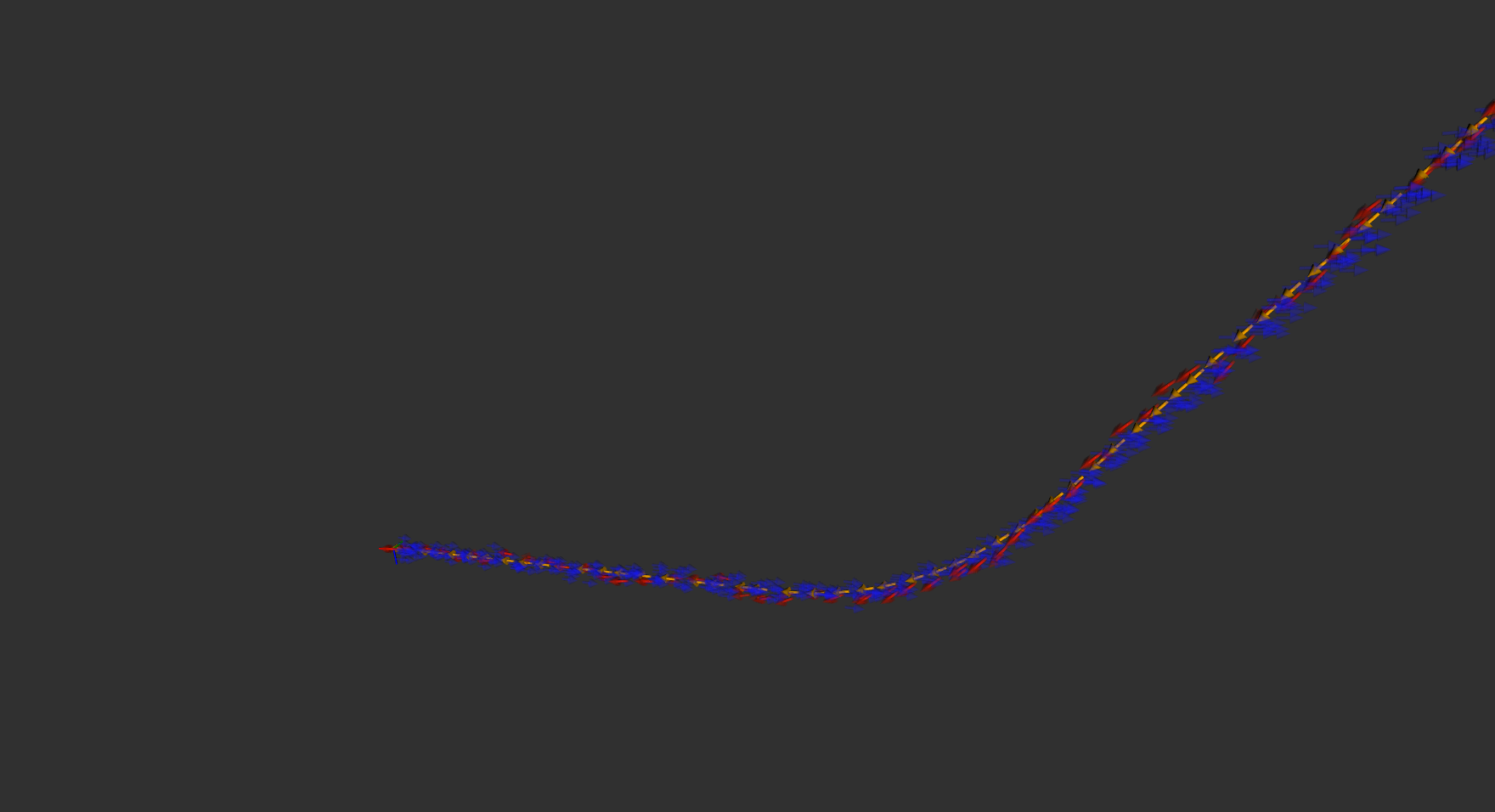
红色为无运动约束,绿色为fused 加入速度观测,蓝色为fused_cons为加入运动约束,可明显看出蓝色曲线大部分时间处于红色曲线之下,说明使用运动约束后,数据的波动性更小。
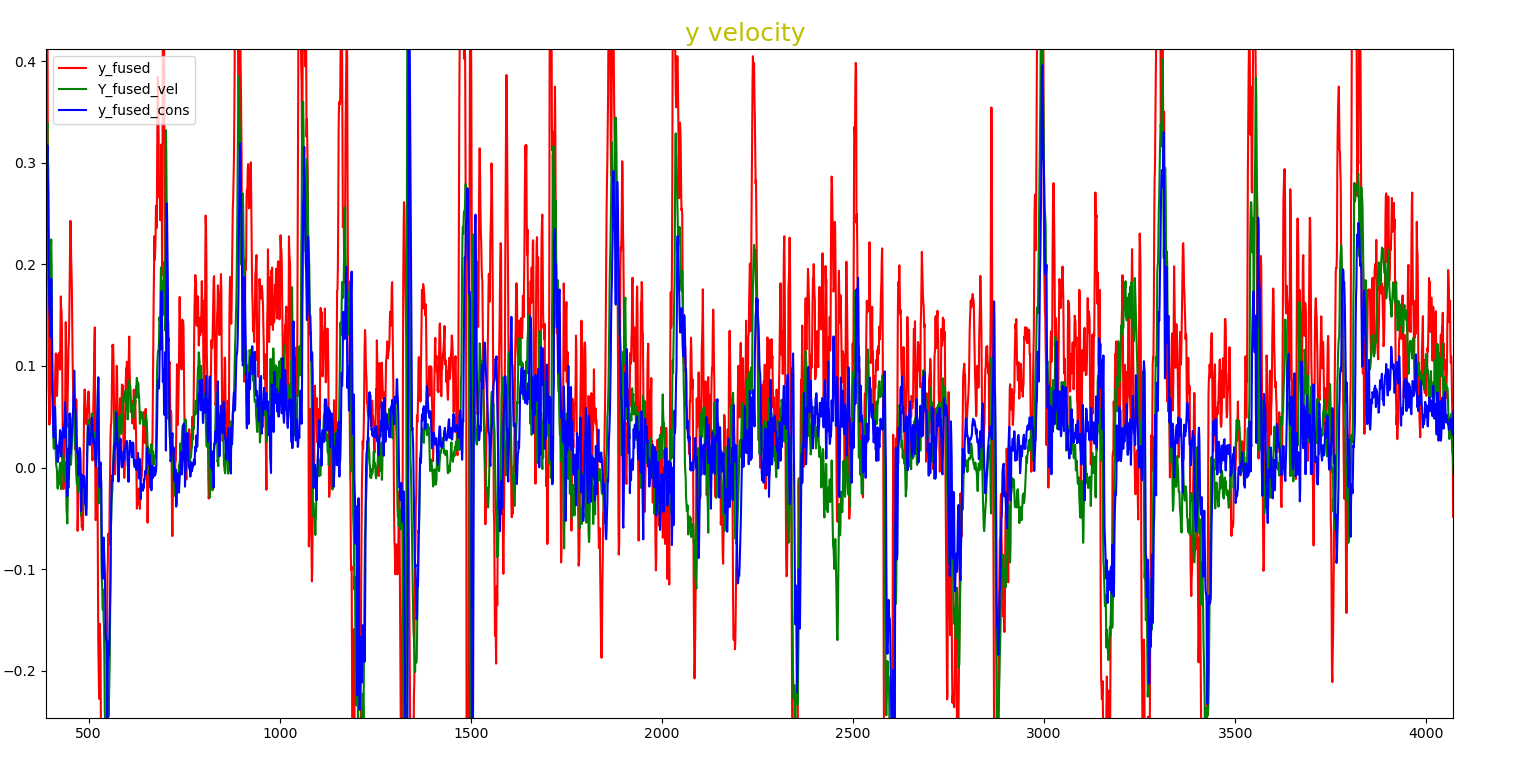
2.4.3 vel_z 比较
红色为无运动约束,绿色为fused 加入速度观测,蓝色为fused_cons为加入运动约束,可明显看出蓝色曲线大部分时间处于红色曲线之下,说明使用运动约束后,数据的波动性更小。
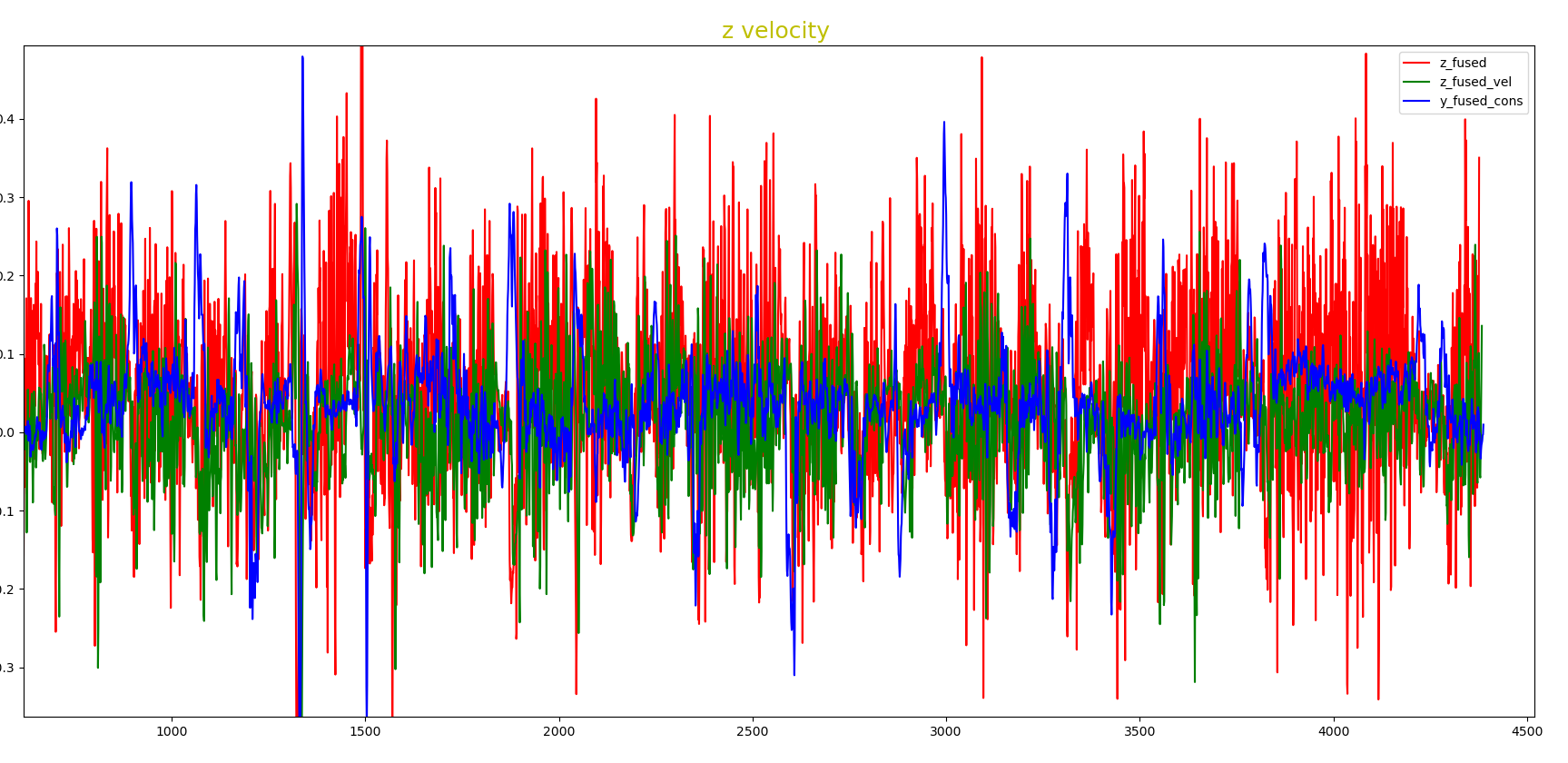
2.4.4 结论
实验结果大致和理论的一致,添加了运动模型后,整体效果有了轻微的改善,但是速度的波动得到了大幅度的抑制!!!
3. GNSS + Oodm 观测模型
参照 (Estimate: imu, Measurment: lidar、odom ) 模型,推导出(Estimate: imu, Measurment: gnss、odom ),观测方程中,gnss 提供position、odom
3.1 公式推导
状态量
δ
x
=
[
δ
p
δ
v
δ
θ
δ
b
a
δ
b
ω
]
\delta \boldsymbol{x}=\left[\begin{array}{l} \delta \boldsymbol{p} \\ \delta \boldsymbol{v} \\ \delta \boldsymbol{\theta} \\ \delta \boldsymbol{b}_{a} \\ \delta \boldsymbol{b}_{\omega} \end{array}\right]
δx=???????δpδvδθδba?δbω?????????
观测量 GPS + Encoder 做观测, GPS 提供position, Encoder 提供velocity
y
=
[
δ
p
 ̄
δ
v
 ̄
b
]
\boldsymbol{y}=\left[\begin{array}{c} \delta \overline{\boldsymbol{p}} \\ \delta \overline{\boldsymbol{v}}^{b} \\ \end{array}\right]
y=[δp?δvb?]
观测值的获取
δ
v
 ̄
b
=
v
~
b
?
v
b
=
R
~
b
w
v
~
w
?
[
v
m
0
0
]
\delta \overline{\boldsymbol{v}}_{b}=\tilde{\boldsymbol{v}}^{b}-\boldsymbol{v}^{b}=\tilde{\boldsymbol{R}}_{b w} \tilde{\boldsymbol{v}}^{w}-\left[\begin{array}{c} \boldsymbol{v}_{m} \\ 0 \\ 0 \end{array}\right]
δvb?=v~b?vb=R~bw?v~w????vm?00????
观测方程
y
=
G
t
δ
x
+
C
t
n
\boldsymbol{y}=\boldsymbol{G}_{t} \delta \boldsymbol{x}+\boldsymbol{C}_{t} \boldsymbol{n}
y=Gt?δx+Ct?n
G t = [ I 3 0 0 0 0 0 R b w [ v b ] × 0 0 ] C t = [ I 3 0 0 I 3 ] \begin{aligned} \boldsymbol{G}_{t} &=\left[\begin{array}{ccccc} \boldsymbol{I}_{3} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{R}_{b w} & {\left[\boldsymbol{v}^{b}\right]_{\times}} & \mathbf{0} & \mathbf{0} \\ \end{array}\right] \\\\\\ \boldsymbol{C}_{t} &=\left[\begin{array}{ccc} \boldsymbol{I}_{3} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{I}_{3} \\ \end{array}\right] \end{aligned} Gt?Ct??=[I3?0?0Rbw??0[vb]×??00?00?]=[I3?0?0I3??]?
n = [ n δ p ˉ x n δ p ˉ y n δ p ˉ z n δ v ˉ x b n δ v ˉ y b n δ v ˉ z b ] T \boldsymbol{n}=\left[\begin{array}{lllllllll} n_{\delta \bar{p}_{x}} & n_{\delta \bar{p}_{y}} & n_{\delta \bar{p}_{z}} & n_{\delta \bar{v}_{x}^{b}} & n_{\delta \bar{v}_{y}^{b}} & n_{\delta \bar{v}_{z}^{b}} \end{array}\right]^{T} n=[nδpˉ?x???nδpˉ?y???nδpˉ?z???nδvˉxb???nδvˉyb???nδvˉzb???]T
3.2 CorrectErrorEstimationPosiVel , 因为只是少了ori这个观测量,所以在(lidar + encoder)的观测上删掉orii这一行的观测就可以。
void ErrorStateKalmanFilter::CorrectErrorEstimationPosiVel( // position + velocity
const Eigen::Matrix4d &T_nb, const Eigen::Vector3d &v_b, const Eigen::Vector3d &w_b,
Eigen::VectorXd &Y, Eigen::MatrixXd &G, Eigen::MatrixXd &K
) {
//
// TODO: set measurement: 计算观测 delta pos 、 delta velocity
//
Eigen::Vector3d v_b_ = {v_b[0], 0, 0}; // measurment velocity (body 系) , 伪观测 (vy 、vz = 0)
Eigen::Vector3d dp = pose_.block<3, 1>(0, 3) - T_nb.block<3, 1>(0, 3);
Eigen::Vector3d dv = pose_.block<3, 3>(0, 0).transpose() *vel_ - v_b ; // delta v , v_x 来自轮速里程计
// TODO: set measurement equation:
YPosiVel_.block<3, 1>(0, 0) = dp; // delta position
YPosiVel_.block<3, 1>(3, 0) = dv; // delta velocity
Y = YPosiVel_;
// set measurement G
GPosiVel_.setZero();
GPosiVel_.block<3, 3>(0, kIndexErrorPos) = Eigen::Matrix3d::Identity();
GPosiVel_.block<3, 3>(3, kIndexErrorVel) = pose_.block<3, 3>(0, 0).transpose();
GPosiVel_.block<3, 3>(3, kIndexErrorOri) = Sophus::SO3d::hat( pose_.block<3, 3>(0, 0).transpose() *vel_ ) ;
G = GPosiVel_;
// set measurement C
CPosiVel_.setIdentity();
Eigen::MatrixXd C = CPosiVel_;
// TODO: set Kalman gain:
Eigen::MatrixXd R = RPosiVel_; // 观测噪声
K = P_ * G.transpose() * ( G * P_ * G.transpose( ) + C * R* C.transpose() ).inverse() ;
}
3.3 参数调整,及重力参数修改
3.3.1 pos vel 观测误差参数调整
FILE: catkin_ws/src/lidar_localization/config/filtering/gnss_ins_sim_filtering.yaml
按照GeYao 助教所说,
最后这里在运行的时候需要提醒一下大家, 左边的两张图是gnss-ins-sim生成测量数据时候的误差等级, 课程中默认使用的都是中等精度, 也就是说gps位置的协方差应该在2.5e-1左右, 而编码器应该在2.5e-3左右, 而右边是我们的作业使用的默认配置文件中的误差等级. 可以看出gps的实际误差与我们给的先验值的差距比较巨大, 这就是为什么有些同学在程序正确的情况下rviz中显示的姿态抖动非常厉害的原因. 建议大家在左边这两个值的基础上进行调参.

所以,我们把 pos 和 vel 的measurment cov 调整为
measurement:
pose:
pos: 1.0e-4
ori: 1.0e-4
pos: 2.5e-1 # 1.0-4
vel: 2.5e-3
3.3.2 重力参数调整
这里生成的仿真数据的重力加速度和kitti的重力加速度方向不太一致,原因,仿真的数据集中传感器的Z轴正方向是朝上的,所以imu_sim_ins accel_z 读出来的数值是 -g。通过 指令rqt_bag 查看传感器读取的重力加速度,写到yaml中。
FILE: catkin_ws/src/lidar_localization/config/filtering/gnss_ins_sim_filtering.yaml
gravity_magnitude: -9.794216
3.3.3 evo评估
# set up session:
source devel/setup.bash
# save odometry:
rosservice call /save_odometry "{}"
# run evo evaluation:
# a. fused 没有输入运动模型 输出评估结果,并以zip的格式存储:
evo_ape kitti ground_truth.txt fused.txt -r full --plot --plot_mode xyz --save_results ./fused.zip
# b. fused_vel 速度观测 输出评估结果,并以zip的格式存储:
evo_ape kitti ground_truth.txt gnss.txt -r full --plot --plot_mode xyz --save_results ./gnss.zip
#e. 比较 laser fused 一并比较评估
evo_res *.zip --use_filenames -p
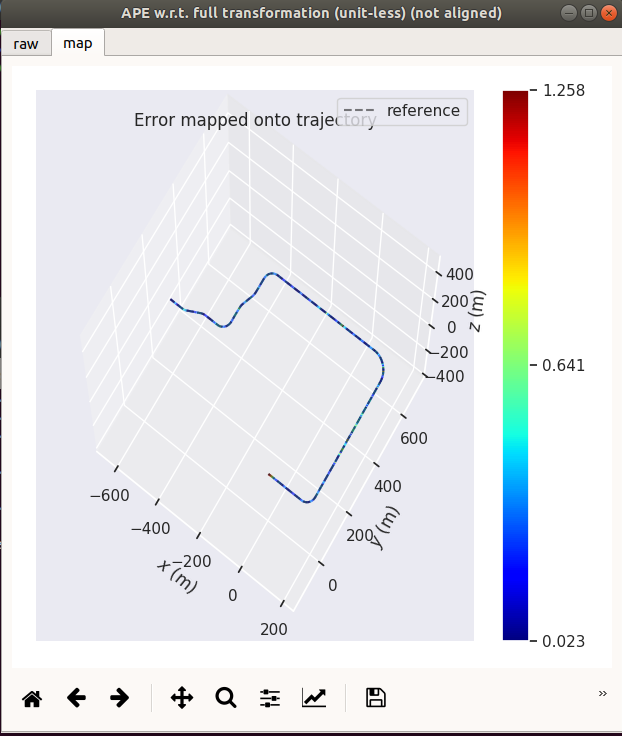
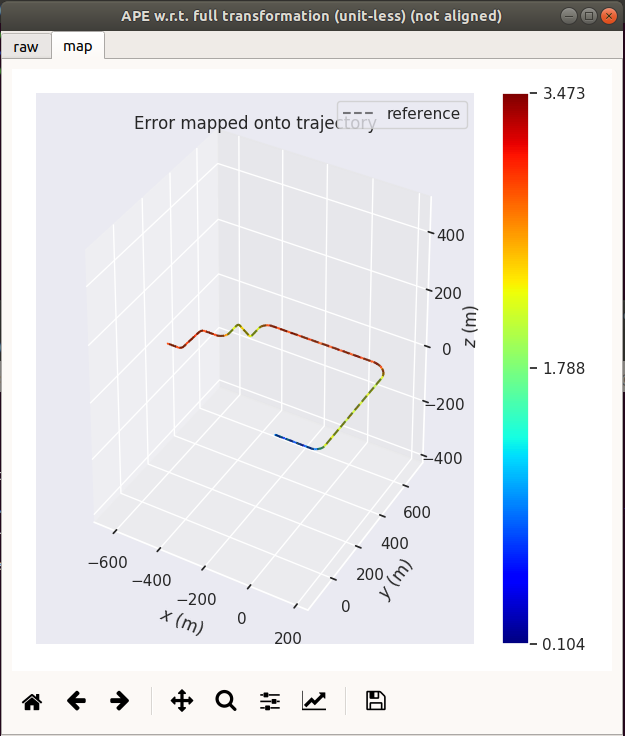
| GNSS + Odom | GNSS Only |
|---|---|
 |  |
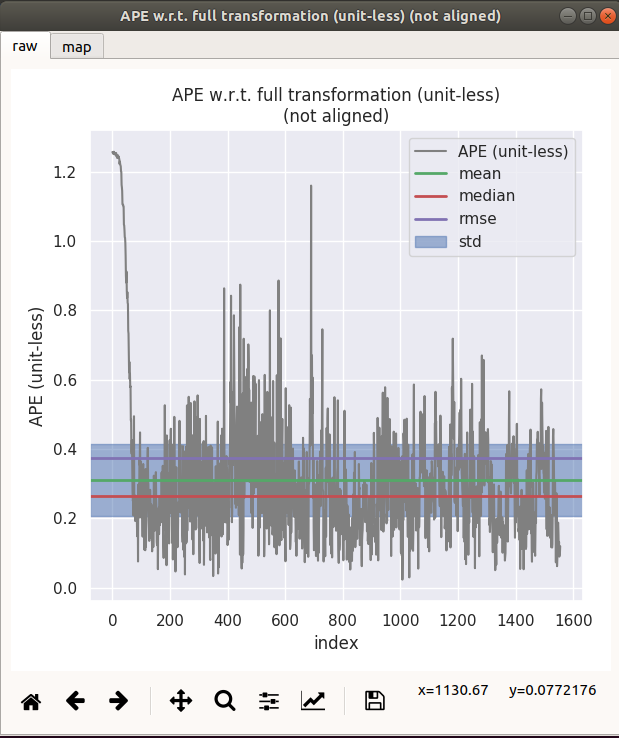 | 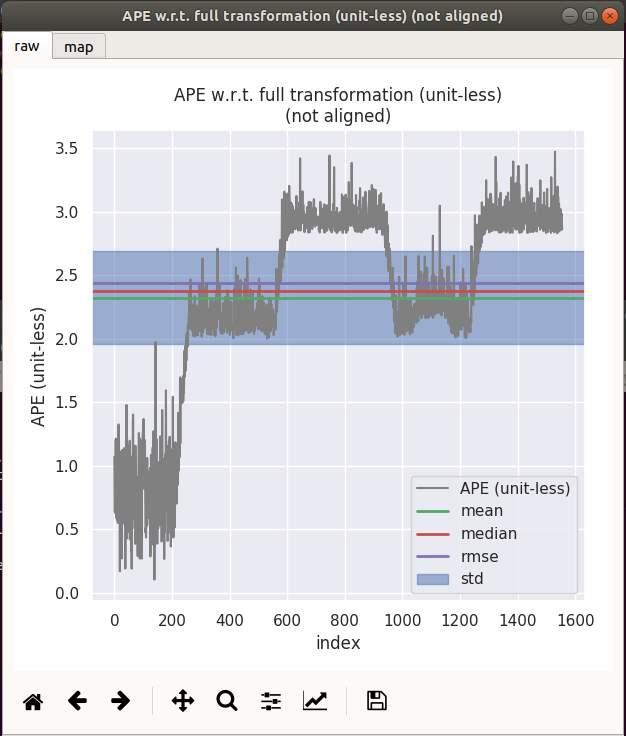 |
| max | mean | median | min | rmse | sse | std | |
|---|---|---|---|---|---|---|---|
| gnss+odom | 1.25794 | 0.31052 | 0.263991 | 0.0234911 | 0.374327 | 218.028 | 0.209041 |
| gnss only | 3.473 | 2.32244 | 2.37926 | 0.103637 | 2.43563 | 9230.62 | 0.733851 |
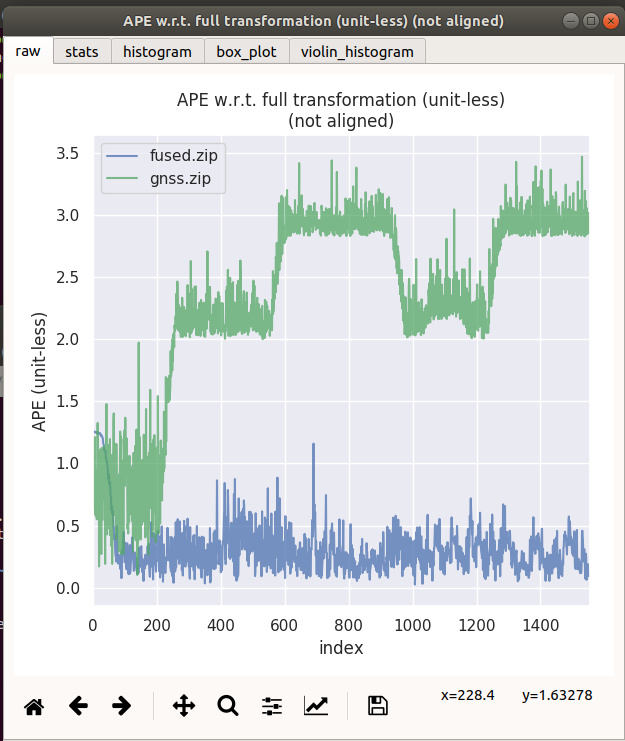
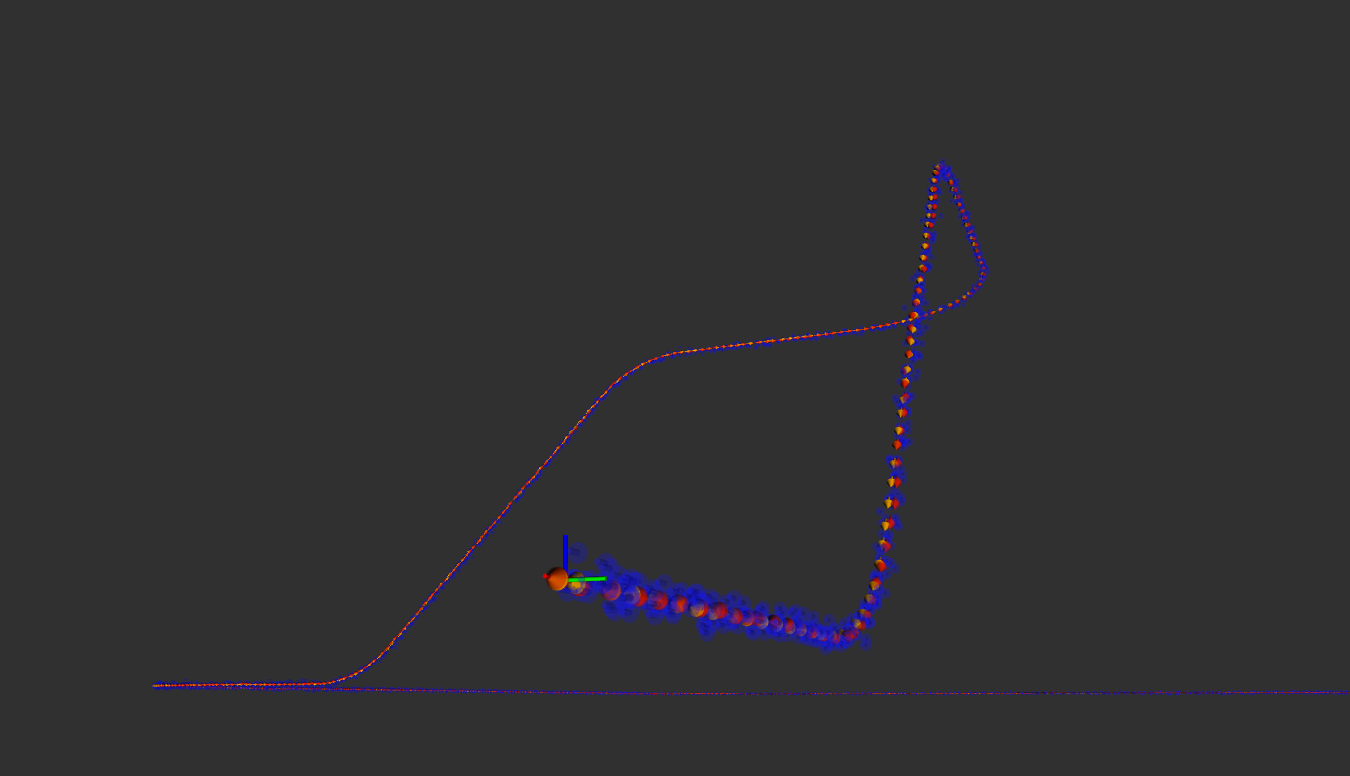
3.4 结论通过对比上述实验
可得知,融合了odom轮速里程计后,数据波动得到大幅度抑制。
? edit by kaho 2021.10.22