基于内容的推荐算法
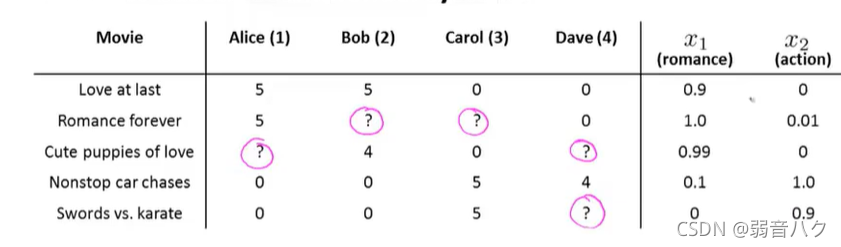
有5个电影,4个人对电影的评分,假设每部电影有2种特征量,即
x
(
i
)
∈
R
(
2
)
x^{(i)} \in R^{(2)}
x(i)∈R(2),如何估算出图中问号的值呢?
我们假设每个用户
j
j
j有一个参数向量
θ
(
j
)
\theta^{(j)}
θ(j),在此例中
θ
(
j
)
∈
R
(
2
)
\theta^{(j)}\in R^{(2)}
θ(j)∈R(2)。用户的参数向量与电影的特证向量维度是相同的。那么与用户对每部电影的评分为:
(
θ
(
j
)
)
T
x
(
i
)
(\theta^{(j)})^{T} x^{(i)}
(θ(j))Tx(i)。
例如第一个用户对第三部电影的预测评分为:

两个向量三维的原因是有一个偏置数,对结果影响不大,暂不考虑。
总结一下条件:

已知:每部电影的特征向量、用户对电影的评价、评分公式:
(
θ
(
j
)
)
T
x
(
i
)
(\theta^{(j)})^{T} x^{(i)}
(θ(j))Tx(i)、求每个用户的参数向量:
θ
(
j
)
\theta^{(j)}
θ(j)。
这就转化为线性回归问题:


最后再使用梯度下降算法或者其他算法求解,得到最终表达式:

在知道每部电影的特征向量,求解每个用户的参数向量,以上就是基于内容的推荐算法。
协同过滤算法
我们把上面的例子调整一下,假设我们不知道每部电影的特征向量,但是我们知道每个打分用户的参数向量
θ
(
j
)
\theta^{(j)}
θ(j)。
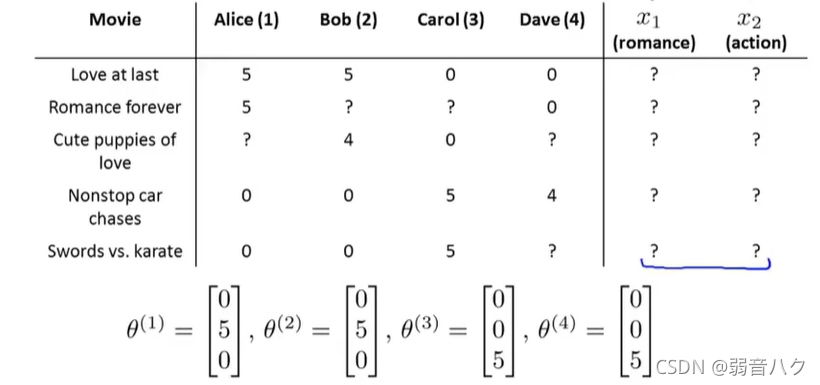
这时候求解每部电影的特征向量
x
(
i
)
x^{(i)}
x(i)。
计算流程和上面基于内容的推荐算法相同,结果如下:

结合两个流程:

两个流程结合就出现这样的情况:先得到
θ
(
j
)
\theta^{(j)}
θ(j)然后求解
x
(
i
)
x^{(i)}
x(i),再求解
θ
(
j
)
\theta^{(j)}
θ(j),这样反复迭代,所以被称为协同过滤。
仔细看两个流程的最后结果的前半部分其实是同一个东西,所以可以得到最终的计算式:

协同过滤算法的总流程:

低秩矩阵分解

假设我们知道
θ
(
j
)
\theta^{(j)}
θ(j),
x
(
i
)
x^{(i)}
x(i),怎么快速计算评分呢?

可以把得分矩阵进行分解:
Y
=
x
θ
T
Y= x \theta^{T}
Y=xθT
如何找到两个相似的电影呢?

均值规范化

假设新加入第五用户,根据最下面的代价函数,此时新用户
θ
(
5
)
\theta^{(5)}
θ(5)应该全是0,此时评分也全是0,这就没有意义了。
那么如何让新用户的0参数向量有意义呢?
使用均值归一化!

然后改变得分公式:
(
θ
(
j
)
)
T
x
(
i
)
+
u
(\theta^{(j)})^{T} x^{(i)} + u
(θ(j))Tx(i)+u
这样即使新用户的参数向量是0向量,它的评分结果也不会是0,而是每个电影的平均得分,这时候就变得有意义。