开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 2021SC@SDUSC基于人工智能的多肽药物分析问题（四） -> 正文阅读

[人工智能]2021SC@SDUSC基于人工智能的多肽药物分析问题（四）

基于人工智能的多肽药物分析问题（四）

2021SC@SDUSC

1. 前言

由于之前未接触过深度学习领域，所以基本所有的代码都得查文档，查api，现在也是一边学习神经网络，一边研究源码。。。而且前两篇直接上手了源码分析，发现漏讲了该方法的具体思路，这周补上。

2. 方法思路

2.1 来自AlphaFold2方法学进展

PS : AlphaFold2目前是小组内另外一名同学的分析内容

从多序列比对（MSA）开始，而不是从更多处理的序列开始特征
用一种更好地表示沿序列相距遥远的残基之间相互作用的注意机制替换二维（2D）卷积
使用双轨网络体系结构，其中1D序列级和2D距离图级的信息进行迭代转换并来回传递，
用SE（3）等变变压器网络直接细化原子坐标（而不是像以前的方法那样细化2D距离图）从双轨网络生成
端到端学习，其中所有网络参数通过反向传播从最终生成的三维坐标通过所有网络层返回到输入序列进行优化

2.2 新思路

rosettafold结合上述五种特性的不同组合的网络结构，尝试了多种方法在网络的不同部分之间传递信息，成功地生成了一个“双轨”网络，信息沿着一维序列对齐轨道和二维距离矩阵轨道并行流动

之后，在双轨的基础上，扩展到在三维坐标空间中运行的第三个轨道。

因而能够在序列、剩余距离和方向以及原子坐标之间提供更紧密的连接，可以实现更好的性能
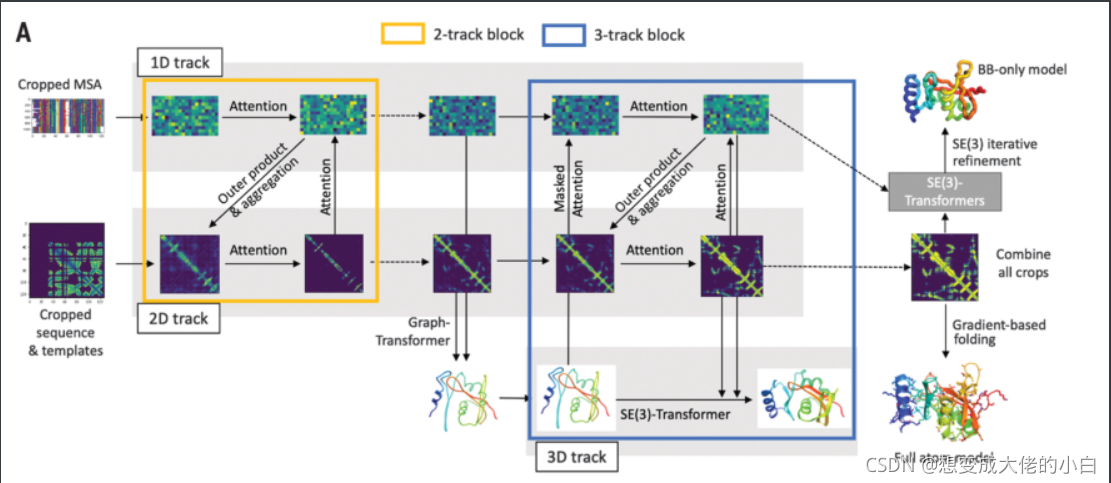
在这里插入图片描述

（在该架构中，信息在1D氨基酸序列信息、2D距离图和3D坐标之间来回流动，从而允许网络集体推理序列内部和之间的关系、距离和坐标）

2.3 限制和解决方法

由于三轨道模型有数百万个参数，收到了计算机硬件内存的限制无法直接在大型蛋白质上训练模型；所以，输入序列的许多不连续片段呈现给网络，这些不连续片段由两个不连续的序列段组成，共跨越260个残基。为了生成最终模型，结合并平均了为每种crops生成的1D特征和2D距离和方向预测，然后使用两种方法生成最终3D结构。

解决方法：

将预测的剩余距离和方向分布输入pyRosetta（5）To generate all-atom模型
将平均的一维和二维特征输入到最终的SE(3)- equivariant Layer(6)，并在从氨基酸序列到三维坐标的端到端训练后，由网络直接生成主干坐标

经过查阅相关资料显示pyrosetta方法要比e2e更精确一些，也就是第一种方法的精确度更高

2.4 看法

rosettafold与AlphaFold2相比来说，在精确度上稍有逊色，这也是公认的事实，但是AlphaFold2所需要的运算资源太苛刻了，平常的计算机难以真正跑相关的模型，RoseTTAFold运算资源相比之下要求低得多，适合平民玩家使用，但是需要的文件大小也着实不小，加起来得有1T+了。另外提一嘴，山大的高性能计算平台就可以跑AlphaFold2的模型。

3. 源码分析

3.0 接上篇博客

def set_neighbors6D(pdict):

    N = pdict['N']
    Ca = pdict['Ca']
    Cb = pdict['Cb']
    nres = pdict['nres']
    
    dmax = 20.0
    
    
    kdCb = scipy.spatial.cKDTree(Cb)
    indices = kdCb.query_ball_tree(kdCb, dmax)
    
    
    idx = np.array([[i,j] for i in range(len(indices)) for j in indices[i] if i != j]).T  # 联系残差指数
    idx0 = idx[0]
    idx1 = idx[1] 
    
    
    dist6d = np.zeros((nres, nres))
    dist6d[idx0,idx1] = np.linalg.norm(Cb[idx1]-Cb[idx0], axis=-1)

   
    omega6d = np.zeros((nres, nres))
    omega6d[idx0,idx1] = get_dihedrals(Ca[idx0], Cb[idx0], Cb[idx1], Ca[idx1])

    
    theta6d = np.zeros((nres, nres))
    theta6d[idx0,idx1] = get_dihedrals(N[idx0], Ca[idx0], Cb[idx0], Cb[idx1])
    
    
    phi6d = np.zeros((nres, nres))
    phi6d[idx0,idx1] = get_angles(Ca[idx0], Cb[idx0], Cb[idx1])
    
    pdict['dist6d'] = dist6d
    pdict['omega6d'] = omega6d
    pdict['theta6d'] = theta6d
    pdict['phi6d'] = phi6d

使用cKDTree进行快速邻居搜索

调用scipy.spatial.cKDTree生成二维样本数据点，然后调用query_ball_tree方法进行快速查找邻点，求自身与他人之间距离不超过r的所有点对，dmax为context中定义的20.0
之后根据得到的点对计算联系残差指数

[[i,j] for i in range(len(indices)) for j in indices[i] if i != j]生成之后转置再保存至idx变量

Cb-Cb距离矩阵

利用 np.zeros生成nres行，nres列的零矩阵，将Cb[idx1]-Cb[idx0]的范数保存至零矩阵的(idx0,idx1)元素中

求Ca-Cb-Cb-Ca二面体的矩阵

定义omega6d为0矩阵，之后对 omega6d[idx0,idx1]这个元素调用了get_dihedrals方法，传入参数为Ca[idx0], Cb[idx0], Cb[idx1], Ca[idx1]：

def get_dihedrals(a, b, c, d):

    b0 = -1.0*(b - a)
    b1 = c - b
    b2 = d - c

    b1 /= np.linalg.norm(b1, axis=-1)[:,None]

    v = b0 - np.sum(b0*b1, axis=-1)[:,None]*b1
    w = b2 - np.sum(b2*b1, axis=-1)[:,None]*b1

    x = np.sum(v*w, axis=-1)
    y = np.sum(np.cross(b1, v)*w, axis=-1)

    return np.arctan2(y, x)

先是对 b0,b1,b2进行初始化赋值。之后，

调用了np.linalg.norm方法，指定了计算向量规范的轴为b1变量的最后一个维度，并使用[:,None]切片操作，对返回的数组增加了一个维度。
调用np.sum方法，对v和w进行赋值
最终求出了x和y，调用np.arctan2，返回了一个n维数组，存储到omega6d[idx0,idx1]变量

求theta矩阵的极坐标

同样是先初始化了一个0矩阵，随后依旧调用了get_dihedrals方法，讲矩阵的极坐标保存至theta6d[idx0,idx1]向量中

求φ矩阵的极坐标

初始化0矩阵phi6d，并调用了get_angles方法，传入Ca[idx0], Cb[idx0], Cb[idx1]参数

def get_angles(a, b, c):
    
    v = a - b
    v /= np.linalg.norm(v, axis=-1)[:,None]
    
    w = c - b
    w /= np.linalg.norm(w, axis=-1)[:,None]
    
    x = np.sum(v*w, axis=1)

    return np.arccos(x)

3.1 set_neighbors3D方法

（由于代码过长，不一次性粘贴，具体分析的时候再粘贴具体代码）

计算得到所有非氢原子的坐标以及类型

    xyz = []
    types = []
    pose = pdict['pose']
    nres = pdict['nres']
    for i in range(1,nres+1):
        r = pose.residue(i)
        rname = r.name()[:3]
        for j in range(1,r.natoms()+1):
            aname = r.atom_name(j).strip()
            name = rname+'_'+aname
            if not r.atom_is_hydrogen(j) and aname != 'NV' and aname != 'OXT' and name in atypes:
                xyz.append(r.atom(j).xyz())
                types.append(atypes[name])

    xyz = np.array(xyz)
    xyz_ca = pdict['Ca']
    lfr = pdict['lfr']

前言：该部分的pdict变量均为前面文章所分析的pdict用一个变量

首先根据传入的参数初始化变量，之后通过两层循环，外层循环获取pose模型内每一个残基，之后对残基的atom_name属性的进行遍历，即相当于rname和aname两个属性之间加上下划线，之后将氢原子的坐标append到xyz变量中，原子类型加入到types变量中。

找到邻间原子并投射到局部参考系上

	dist = 14.0
    kd = scipy.spatial.cKDTree(xyz)
    kd_ca = scipy.spatial.cKDTree(xyz_ca)
    indices = kd_ca.query_ball_tree(kd, dist)
    idx = np.array([[i,j,types[j]] for i in range(len(indices)) for j in indices[i]])

    xyz_shift = xyz[idx.T[1]] - xyz_ca[idx.T[0]]
    xyz_new = np.sum(lfr[idx.T[0]] * xyz_shift[:,None,:], axis=-1)

调用scipy库的scipy.spatial.cKDTree方法生成二维样本数据点，之后query_ball_tree寻找之前存储的xyz变量的邻点，之后根据得到的点对计算联系残差指数idx。之后计算了xyz_shift，xyz_new

    nbins = 24
    width = 19.2
    N = idx.shape[0]
    h = width / (nbins-1)

    xyz = (xyz_new + 0.5 * width) / h

    # residue indices
    i = idx[:,0].astype(dtype=np.int16).reshape((N,1))
    
    # atom types
    t = idx[:,2].astype(dtype=np.int16).reshape((N,1))
    
    # discretized x,y,z coordinates
    klm = np.floor(xyz).astype(dtype=np.int16)

    # atom coordinates in the cell it occupies
    d = xyz - np.floor(xyz)

进行离散化，定义变量nbins，width并初始化
N表示总的邻居数
将所有邻点移到中心，并将坐标按h缩放
调用astype()，将idx数据的副本再转化为指定的类型，其中i表示残差指数，t表示原子的种类
之后调用np.floor()方法离散x，y，z坐标
再用移至中心点后缩放过的xyz变量减去np.floor(xyz)，得到原子在他所占据的单元格内的坐标

再进行三线性插值

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KhrPqUlc-1634903231781)(C:\Users\你好\AppData\Roaming\Typora\typora-user-images\image-20211022191415371.png)]$

b = a[(np.min(a[:,1:4],axis=-1) >= 0) & (np.max(a[:,1:4],axis=-1) < nbins) & (a[:,5]>1e-5)]

pdict['idx'] = b[:,:5].astype(np.uint16)
pdict['val'] = b[:,5].astype(np.float16)

最后将得到的b相应的切片赋值给pdict变量

3.2 set_features1D方法

def set_features1D(pdict):传入参数pdict

进行β-strand 配对

β[折叠]链（β-strand，beta-strand）是2009年公布的细胞生物学名词，蛋白质二级结构的基本类型之一，外观伸展并稍有折叠。

是蛋白质的二级结构，肽键平面折叠成锯齿状，相邻肽链主链的N-H和C=O之间形成有规则的氢键，在β-折叠中，所有的肽键都参与链间氢键的形成，氢键与β-折叠的长轴呈垂直关系。

蛋白质二级结构数据库

—来自百度百科

    DSSP = pyrosetta.rosetta.core.scoring.dssp.Dssp(p)
    bbpairs = np.zeros((nres, nres)).astype(np.uint8)
    for i in range(1,nres+1):
        for j in range(i+1,nres+1):
            # parallel
            if DSSP.paired(i,j,0):
                bbpairs[i,j] = 1
                bbpairs[j,i] = 1
            # anti-parallel
            elif DSSP.paired(i,j,1):
                bbpairs[i,j] = 2
                bbpairs[j,i] = 2
    
    abc = np.array(list("BEGHIST "), dtype='|S1').view(np.uint8)
    dssp8 = np.array(list(DSSP.get_dssp_unreduced_secstruct()),
                     dtype='|S1').view(np.uint8)
    for i in range(abc.shape[0]):
        dssp8[dssp8 == abc[i]] = i
    dssp8[dssp8 > 7] = 7

DSSP声明为pyrosetta.rosetta.core.scoring.dssp.Dssp这个类，bbpairs声明为0矩阵，之后一个二重循环遍历矩阵，调用DSSP.paired方法，传入三个参数，前两个参数表示坐标，最后一个参数为bool值，如果是parallel，那么将bbpairs这一矩阵相应位置以及相应的转置位置都置为1，反之，则置为2.
定义abc
dssp8的定义调用了get_dssp_unreduced_secstruct方法，将返回的dssp结构字符串强制类型转换为数组

将三态的DSSP映射到0，1，2三个整数

DSSP = pyrosetta.rosetta.core.scoring.dssp.Dssp(p)
abc = np.array(list("EHL"), dtype='|S1').view(np.uint8)
dssp3 = np.array(list(DSSP.get_dssp_secstruct()), 
                 dtype='|S1').view(np.uint8)
for i in range(abc.shape[0]):
    dssp3[dssp3 == abc[i]] = i
dssp3[dssp3 > 2] = 2

和前面一样，先声明Dssp实例，再调用get_dssp_secstruct方法得到结构（返回字符串类型），最后遍历dssp3数组并将字符mapping为0，1，2数字

alphabet = np.array(list("ARNDCQEGHILKMFPSTWYV-"), dtype='|S1').view(np.uint8)
seq = np.array(list(p.sequence()), dtype='|S1').view(np.uint8)
for i in range(alphabet.shape[0]):
    seq[seq == alphabet[i]] = i

上述这一块代码将ARNDCQEGHILKMFPSTWYV这些字母转化为了数字，（便于后面训练模型）

    phi = np.array(np.deg2rad([p.phi(i) for i in range(1, nres+1)])).astype(np.float32)
    psi = np.array(np.deg2rad([p.psi(i) for i in range(1, nres+1)])).astype(np.float32)

    # termini & linear chainbreaks
    mask1d = np.ones(nres).astype(np.bool)
    mask1d[0] = mask1d[-1] = 0
    for i in range(1,nres):
        A = p.residue(i).atom('CA')
        B = p.residue(i+1).atom('CA')
        if (A.xyz() - B.xyz()).norm() > 4.0:
            mask1d[i-1] = 0
            mask1d[i] = 0

linear chainbreaks翻译过来是线性链断裂，具体原理暂时不是很明白，涉及别的学科了。。代码方面还是比较简单易懂

最后，将相应的变量都存储至pdict中

    pdict['seq'] = seq
    pdict['dssp8'] = dssp8
    pdict['dssp3'] = dssp3
    pdict['phi'] = phi
    pdict['psi'] = psi
    pdict['mask1d'] = mask1d
    pdict['bbpairs'] = bbpairs