图像阈值化,是指根据图像内像素点强度的分布规律设置一个阈值,并根据像素点强度高于阈值或者低于阈值而进行一些处理。例如,输入是一张灰度图和一个阈值 T T T,当图中像素值大于阈值 T T T,则输出图像对应像素设置为255(白色);当图中像素值小于等于阈值 T T T,则输出图像对应像素设置为0(黑色),这样通过阈值化就得到了一个二值化的图像。阈值化作为一种非常普遍使用的图像预处理方式,有利于我们在图像中定位到我们的目标对象。
从上述阈值化的定义中,我们会发现存在两个关键问题:
- 合适的阈值如何设置?
- 阈值设置后,基于像素点与阈值的关系而进行的处理方式都有哪些?
1. 手动设置阈值
最简单粗暴的方式莫过于手动设置阈值。当我们拿到一张彩色图像并转换到灰度图后,我们可以打印出灰度图每个图像位置的灰度值。我们可以不断地尝试阈值,从而使得我们的目标对象被提取地很好。
在OpenCV中提供了阈值化的函数
double cv::threshold ( InputArray src,
OutputArray dst,
double thresh,
double maxval,
int type
)
| 参数 | 参数含义 |
|---|---|
| src | 输入图像(支持多通道) |
| dst | 输出图像 |
| thresh | 手动设置的阈值 |
| maxval | 图像像素的最大值 |
| type | 阈值处理的方式,见下图 |

c++示例代码
// 原始图像
Mat src = imread("/home/user/1.jpg");
// 转为灰度图
Mat gray;
cvtColor(src, gray, COLOR_BGR2GRAY);
// 阈值化,像素点强度>200的设置为255,小于等于200的设置为0
Mat bw;
threshold(gray, bw, 200, 255, THRESH_BINARY);
手动设置阈值在针对一张特定图像的处理时,虽然我们会尝试若干次,但通常我们还是可以基本找到一个理想的值。但它的主要弊端是它的泛化值不好,可能在这张图像上效果很不错,换到另一张图像效果就大打折扣,原因可能只是另一张图像拍摄的光线、角度稍有不同等等。
因此我们需要有一种自动确定阈值的方法,能根据图像中像素强度的规律,找到一个合理的阈值。
2. OTSU 大津阈值法
大津阈值法假定图像中包含前景像素和背景像素,于是它计算能够将两类像素分类的最佳阈值,从而使得它们的类内方差最小,并证明了类内方差最小等价于类间方差最大。
为了形象的说明大津阈值法的效果,我们先举一个例子,让大家有一个直观的理解,最后我们会给出严谨的证明。
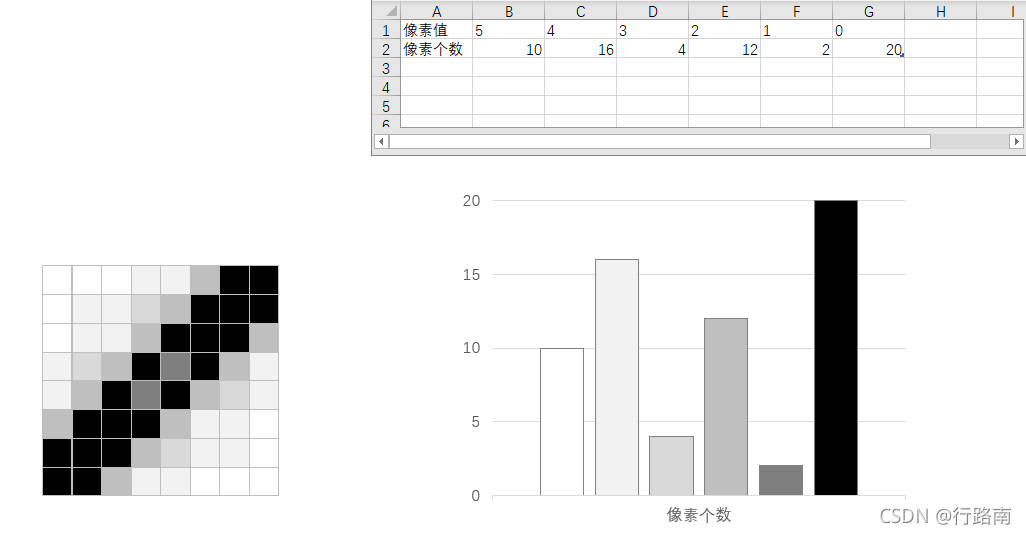
大津算法,是逐一计算每个阈值下的最小类内方差,找到最小的类内方差的阈值就是我们期望的阈值。
咱们以阈值 T = 3 T=3 T=3为例,来计算该阈值下的类内方差。
- 像素值小于等于3的为背景,背景像素的像素数量权重 w b w_b wb?、灰度均值 μ b \mu_b μb?和灰度方差 σ b 2 \sigma_b^2 σb2?计算如下:
n b = 20 + 2 + 12 + 4 = 38 n = 8 ? 8 = 64 w b = n b n = 38 64 μ b = 0 ? 20 + 1 ? 2 + 2 ? 12 + 3 ? 4 n b = 38 38 = 1 σ b 2 = ( 0 ? μ b ) 2 ? 20 + ( 1 ? μ b ) 2 ? 2 + ( 2 ? μ b ) 2 ? 12 + ( 3 ? μ b ) 2 ? 4 n b = 48 38 = 1.26 n_b = 20 + 2 + 12 + 4 = 38 \\ n = 8 * 8 = 64 \\ w_b = \frac{n_b}{n} = \frac{38}{64} \\ \mu_b = \frac{0 * 20 + 1 * 2 + 2 * 12 + 3 * 4}{n_b} = \frac{38}{38} = 1\\ \sigma_b^2 = \frac{(0-\mu_b)^2 * 20 +(1-\mu_b)^2 * 2+(2-\mu_b)^2 * 12 +(3-\mu_b)^2*4}{n_b} = \frac{48}{38} = 1.26 nb?=20+2+12+4=38n=8?8=64wb?=nnb??=6438?μb?=nb?0?20+1?2+2?12+3?4?=3838?=1σb2?=nb?(0?μb?)2?20+(1?μb?)2?2+(2?μb?)2?12+(3?μb?)2?4?=3848?=1.26
- 像素值大于3的为前景,前景像素的像素数量权重 w f w_f wf?、灰度均值 μ f \mu_f μf?和灰度方差 σ f 2 \sigma_f^2 σf2?计算如下:
n f = 16 + 10 = 26 w f = n f n = 24 64 μ f = 4 ? 16 + 5 ? 10 n f = 114 24 σ f 2 = ( 4 ? μ f ) 2 ? 16 + ( 5 ? μ f ) 2 ? 10 n f = 9.625 24 = 0.4 n_f =16 + 10 = 26 \\ w_f = \frac{n_f}{n} = \frac{24}{64} \\ \mu_f = \frac{4 * 16 + 5 * 10}{n_f} = \frac{114}{24}\\ \sigma_f^2 = \frac{(4-\mu_f)^2 * 16 +(5-\mu_f)^2 * 10}{n_f} = \frac{9.625}{24} = 0.4 nf?=16+10=26wf?=nnf??=6424?μf?=nf?4?16+5?10?=24114?σf2?=nf?(4?μf?)2?16+(5?μf?)2?10?=249.625?=0.4
- 根据背景的灰度方差
σ
b
2
\sigma_b^2
σb2? 和
σ
f
2
\sigma_f^2
σf2? 和对应的权重
w
b
w_b
wb? 和
w
f
w_f
wf?, 求得类内方差为:
σ T 2 = w b ? σ b 2 + w f ? σ f 2 = 0.898 \sigma_T^2 = w_b*\sigma_b^2 + w_f * \sigma_f^2 = 0.898 σT2?=wb??σb2?+wf??σf2?=0.898
以上是阈值设置为3的类内方差计算过程,同理我们可以计算阈值从0到5的全部类内方差,找到最小的类内方差对应的阈值即可。
实际上,大津算法证明的是最小化类内方差是等价于最大化类间方差,从而利用最大化类间方差,产生了一个比上述过程更简便,能够迭代计算的高效算法。
以下是证明过程(不感兴趣的可以跳过)。
已知条件:
h ( i ) h(i) h(i): 像素值为 i i i的像素数量, i = 0 , 1 , 2 , . . . , 255 i= 0,1,2,...,255 i=0,1,2,...,255
n b n_b nb? : 背景像素的像素数量 n b = ∑ i = 0 T h ( i ) n_b = \sum_{i=0}^T h(i) nb?=∑i=0T?h(i);
n f n_f nf? : 前景像素的像素数量 n f = ∑ i = T + 1 255 h ( i ) n_f = \sum_{i=T+1}^{255} h(i) nf?=∑i=T+1255?h(i);
n n n : 图像像素的像素数量总数 n = n b + n f n=n_b+n_f n=nb?+nf?
w b w_b wb? : 背景像素的像素数量权重 w b = n b / n w_b = n_b / n wb?=nb?/n;
w f w_f wf? : 前景像素的像素数量权重 w f = n f / n = 1 ? w b w_f = n_f / n = 1- w_b wf?=nf?/n=1?wb?
g ( i ) g(i) g(i): 像素值为 i i i的像素数量在所在区域的比例,即当 i i i属于背景, g ( i ) = h ( i ) / n b g(i) = h(i) / n_b g(i)=h(i)/nb?; 当 i i i属于前景,有 g ( i ) = h ( i ) / n f g(i) = h(i) / n_f g(i)=h(i)/nf?
p ( i ) p(i) p(i): 像素值为 i i i的像素数量在整个图像的比例,即 p ( i ) = h ( i ) / n p(i) = h(i) / n p(i)=h(i)/n
μ b \mu_b μb? : 背景像素的灰度均值 μ b = ∑ i = 0 T i ? h ( i ) n b = ∑ i = 0 T g ( i ) ? i \mu_b = \frac{\sum_{i=0}^T i * h(i) }{n_b} = \sum_{i=0}^T g(i) * i μb?=nb?∑i=0T?i?h(i)?=∑i=0T?g(i)?i;
μ f \mu_f μf? : 前景像素的灰度均值 μ f = ∑ i = T + 1 255 i ? h ( i ) n f = ∑ i = T + 1 255 g ( i ) ? i \mu_f = \frac{\sum_{i=T+1}^{255} i * h(i) }{n_f} = \sum_{i=T+1}^{255} g(i) * i μf?=nf?∑i=T+1255?i?h(i)?=∑i=T+1255?g(i)?i;
μ \mu μ : 图像像素的总灰度均值 μ = w b ? μ b + w f ? μ f \mu = w_b * \mu_b + w_f * \mu_f μ=wb??μb?+wf??μf?
σ b 2 \sigma^2_b σb2? : 背景像素的灰度方差 σ b 2 = E ( x 2 ) ? E ( x ) 2 = ∑ i = 0 T g ( i ) ? i 2 ? μ b 2 \sigma^2_b = E(x^2) - E(x)^2 = \sum_{i=0}^T g(i) * i^2 - \mu_b^2 σb2?=E(x2)?E(x)2=∑i=0T?g(i)?i2?μb2?
σ f 2 \sigma^2_f σf2? : 前景像素的灰度方差 σ f 2 = ∑ i = T + 1 255 g ( i ) ? i 2 ? μ f 2 \sigma^2_f = \sum_{i=T+1}^{255} g(i) * i^2 - \mu_f^2 σf2?=∑i=T+1255?g(i)?i2?μf2?
σ 2 \sigma^2 σ2 : 图像像素的灰度方差 σ 2 = ∑ i = 0 255 p ( i ) ? i 2 ? μ 2 \sigma^2 = \sum_{i=0}^{255} p(i) * i^2 - \mu^2 σ2=∑i=0255?p(i)?i2?μ2
且类内方差和类间方差的定义为:
σ i n 2 \sigma_{in}^2 σin2? : 图像像素的类内方差 $\sigma_{in}^2 = w_b * \sigma_b^2 + w_f * \sigma_f^2 $
σ o u t 2 \sigma^2_{out} σout2? : 图像像素的类间方差 $\sigma_{out}^2 = w_b * (\mu_b - \mu)^2 + w_f * (\mu_f - \mu)^2 $
求证:
最小化类内方差 σ i n 2 \sigma_{in}^2 σin2?等价于最大化类间方差 σ o u t 2 \sigma^2_{out} σout2?
证明过程:

因为 σ 2 \sigma^2 σ2 是一个定值,因此最小化 σ i n 2 \sigma^2_{in} σin2? 等价于最大化 σ o u t 2 \sigma^2_{out} σout2?
证明完毕。
在OpenCV中对于大津算法阈值化的函数和手动阈值法是一个函数
double cv::threshold ( InputArray src,
OutputArray dst,
double thresh,
double maxval,
int type
)
区别在于最后一个参数不仅要指定要处理的方式(上述介绍的THRESH_BINARY 等五种方式),还需要指定是大津算法THRESH_OTSU。
具体代码示意如下:
// 原始图像
Mat src = imread("/home/user/1.jpg");
// 转为灰度图
Mat gray;
cvtColor(src, gray, COLOR_BGR2GRAY);
// 阈值化,指定了处理方式和大津算法,此时会自动计算出阈值而代替手动指定的阈值,即此时50不起作用
Mat bw;
threshold(gray, bw, 50, 255, THRESH_BINARY | THRESH_OTSU);
3 局部自适应阈值化法
上述介绍的两种阈值化方法都是针对全局图像有一个唯一的阈值;本节介绍的是当一副图像的不同区域具有不同的亮度时,所实现的针对每个区域的自适应阈值方法。具体原理是设置一个区域块大小,每一块区域计算出一个阈值,从而在图像亮度不同时得到一个很好的效果。
在OpenCV中的函数是:
void cv::adaptiveThreshold ( InputArray src,
OutputArray dst,
double maxValue,
int adaptiveMethod,
int thresholdType,
int blockSize,
double C
)
Parameters
| src | 仅支持单通道图像 |
|---|---|
| dst | 输出图像 |
| maxValue | 为满足条件的像素指定的非零值 |
| adaptiveMethod | 支持两种自适应阈值方法,在下文详细介绍。 |
| thresholdType | 自适应类型只支持THRESH_BINARY 和 THRESH_BINARY_INV两种。这两种在上文第一节中有详细介绍。 |
| blockSize | 用于计算像素阈值的像素邻域的大小: 3、5、7等等。 |
| C | 从平均数或加权平均数减去常数(详见下文) |
adaptiveMethod 方法由两种:
- ADAPTIVE_THRESH_MEAN_C : b l o c k ? b l o c k block * block block?block的邻域内的均值减去常数C即得到局部阈值
- ADAPTIVE_THRESH_GAUSSIAN_C : b l o c k ? b l o c k block * block block?block的邻域内的加权和减去常数C即得到局部阈值
// 原始图像
Mat src = imread("/home/user/1.jpg");
// 转为灰度图
Mat gray;
cvtColor(src, gray, COLOR_BGR2GRAY);
// 自适应阈值化
Mat bw;
cv::adaptiveThreshold(gray, bw, 255, adaptiveMethod, THRESH_BINARY, 3, 1);
参考资料
https://docs.opencv.org/master/d7/d1b/group__imgproc__misc.html#ga72b913f352e4a1b1b397736707afcde3
https://docs.opencv.org/master/d7/d1b/group__imgproc__misc.html#gae8a4a146d1ca78c626a53577199e9c57
https://zh.wikipedia.org/wiki/%E5%A4%A7%E6%B4%A5%E7%AE%97%E6%B3%95
https://github.com/opencv/opencv/blob/master/modules/imgproc/src/thresh.cpp
https://cloud.tencent.com/developer/article/1084244
