文章目录
第二周 优化算法
2.1 Mini-batch 梯度下降
把样本再分为小批量的样本,在梯度下降时,用这小批量的样本的梯度代替整体梯度进行梯度下降的方法。
这样,我们得到的cost function随着迭代进行的曲线并不是一直下降,而是波动下降。
当mini-batch的大小为1,我们就得到了随机梯度下降算法(Stochastic Gradient Descent)。
2.2 指数加权平均数 Exponentially weighted averages
直接给出公式:
v t = β v t ? 1 + ( 1 ? β ) θ t v_t=\beta v_{t-1}+(1-\beta)\theta_t vt?=βvt?1?+(1?β)θt?,其中 θ \theta θ 是原数据,v是经过计算后的数据。
本质就是以指数式递减加权的移动平均。各数值的加权而随时间而指数式递减,越近期的数据加权越重,但较旧的数据也给予一定的加权。
2.3 指数加权平均数的修正
计算移动平均数的时候,初始化𝑣0 = 0,𝑣1 = 0.98𝑣0 + 0.02𝜃1,但是𝑣0 = 0,所以这部 分没有了(0.98𝑣0),所以𝑣1 = 0.02𝜃1,所以如果一天温度是 40 华氏度,那么𝑣1 = 0.02𝜃1 = 0.02 × 40 = 8,因此得到的值会小很多,所以第一天温度的估测不准。
有个办法可以修改这一估测,让估测变得更好,更准确,用 v t ′ = v t 1 ? β t v_t^\prime = \frac{v_t}{1-\beta^t} vt′?=1?βtvt?? ,t 就是现在的天数。相当于给原来的vt乘上一个大于1的数修正。
在机器学习中,在计算指数加权平均数的大部分时候,大家不在乎执行偏差修正,因为 大部分人宁愿熬过初始时期,拿到具有偏差的估测,然后继续计算下去。如果你关心初始时 期的偏差,在刚开始计算指数加权移动平均数的时候,偏差修正能帮助你在早期获取更好的 估测。
2.4 动量梯度下降法 Gradient descent with Momentum
动量梯度下降法就是将指数加权平均用到梯度下降的过程。

在上图中你会发现,纵轴的摆动很大,但平均值为0;横轴的摆动很小,都指向中心方向。
如果我们对历史梯度进行加权平均,我们就能一定程度上消除纵轴摆动过大的缺点,加快横轴的运动。

2.6 RMSprop 算法
root mean square prop 均方根传播算法
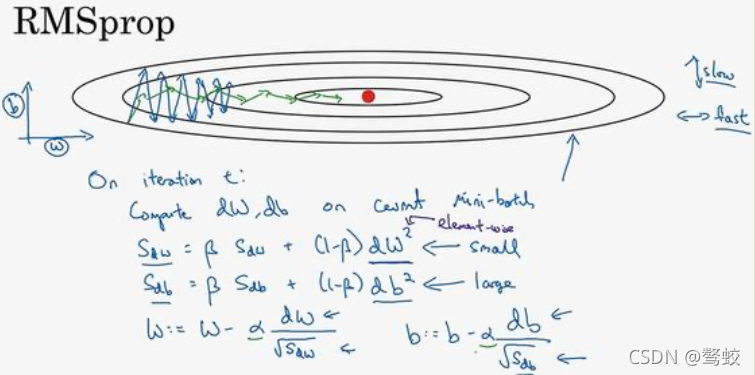
我的理解:平方加剧了方向上的摆动。最后梯度更新时,再除以方根,结果就是摆动大的维度除以一个较大的数,消除了影响。
要说明一点,我一直把纵轴和横轴方向分别称为𝑏和𝑊,只是为了方便展示而已。实际中,你会处于参数的高维度空间,所以需要消除摆动的垂直维度,你需要消除摆动,实际上是参数𝑊 ,𝑊 等的合集,水平维度可能𝑊 ,𝑊 等等,因此把𝑊和𝑏分开只是方便说明。
实际中𝑑𝑊是一个高维度的参数向量,𝑑𝑏也是一个高维度参数向量,但是你的直觉是,在你要消除摆动的维度中,最终你要计算一个更大的和值,这个平方和微分的加权平均值,所以你最后去掉了那些有摆动的方向。所以这就是 RMSprop,全称是均方根,因为你将微分进行平方,然后最后使用平方根。
2.7 Adam 优化算法 Adaptive Moment Estimation

Adam 算法结合了 Momentum 和 RMSprop 梯度下降法,并且是一种极其常用的学 习算法,被证明能有效适用于不同神经网络,适用于广泛的结构。
2.8 学习率衰减
你可以将学习率设置为 $a=\frac{1}{1+decay_rate\times epoch_num}a_0 $ ,其中 decay_rate是衰减率,epoch_num是代数,a0是初始学习率。这个衰减率是另外一个你需要调整的超参数。
还有许多其他 学习率衰减公式。
2.9 局部最优问题
在神经网络优化中,我们遇到的局部最优往往都是鞍点。
我们从深度学习历史中学到的一课就是,我们对低维度空间的大部分直觉,比如你 可以画出上面的图,并不能应用到高维度空间中
首先,你不太可能困在极差的局部最优中,条件是你在训练较大的神经网络,存在大量参数,并且成本函数𝐽被定义在较高的维度空间。
第二点,平稳段是一个问题,这样使得学习十分缓慢,这也是像 Momentum 或是 RMSprop,Adam 这样的算法,能够加速学习算法的地方。在这些情况下,更成熟的优化算法,如 Adam 算法,能够加快速度,让你尽早往下走出平稳段。