[人工智能]一元函数微分的python实现(上)

本博文源于高等数学用python实现，包含了变量与函数，如何利用python进行基本数学运算，也包含了如何利用python绘制平面曲线，效果非常不错，可方便收藏，代码+效果，简短而高效，可方便修改，也可随手复制。

实验一：变量与函数

1.将0.182赋值给x，将0.225赋值给y

>>> x,y = 0.182,'hello'
>>> x
0.182
>>> y
'hello'
>>>

2.调用math标准库，计算$\sin \frac{\pi }{2}$

>>> import math
>>> math.sin(math.pi/2)
1.0
>>>

3.自定义函数，返回用户输入实数的绝对值

>>> def main():
...     a = input("Enter a number:")
...     print(fabs(float(a)))
...
>>> main()
Enter a number:23
23.0
>>> main()
Enter a number:-12
12.0
>>>

实验二: 利用python进行基本数学运算

1.直接输入并计算$(1.5{)}^3?\frac{1}{3}\sin \pi +\sqrt{5}$

>>> from math import sin,sqrt,pi
>>> 1.5**3-sin(pi)/3+sqrt(5)
5.61106797749979
>>>

2.设球的半径为r=2,求球的体积$V=\frac{4}{3}\pi r^3$

>>> from math import pi
>>> r = 2
>>> v = 4/3*pi*pow(r,3)
>>> v
33.510321638291124
>>>

3. 求$y_1=\frac{2sin(0.3\pi )}{1+\sqrt{5}},y_2=\frac{2cos(0.3\pi )}{1+\sqrt{5}}$

>>> from math import sin,cos,sqrt,pi
>>> y1 = 2 * sin(0.3*pi)/(1+sqrt(5))
>>> y2 = 2 * cos(0.3*pi)/(1+sqrt(5))
>>> print('y1=',y1,';y2=%.2f'%y2)
y1= 0.5 ;y2=0.36
>>>

实验三：利用Python绘制平面曲线

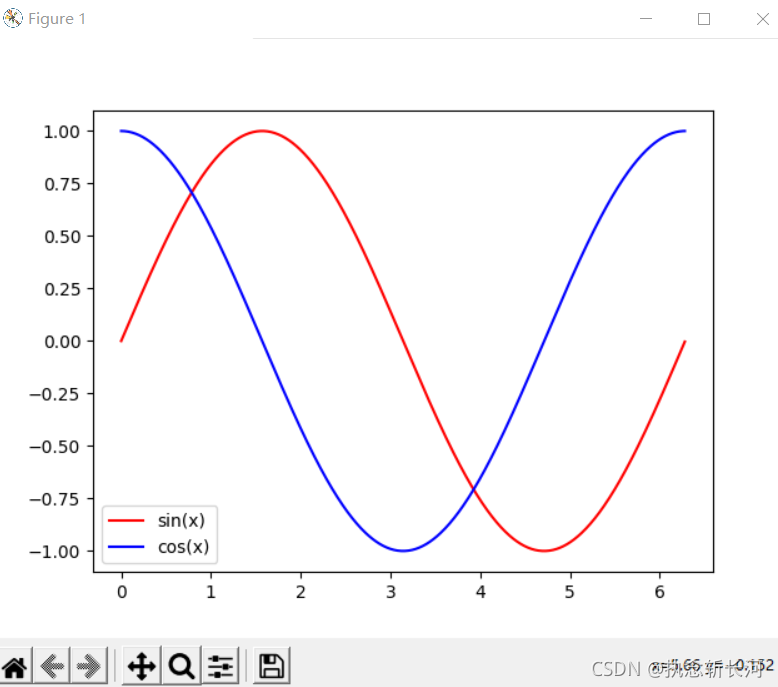
3.1 同时绘制函数y=sinx和y=cos的图像

import  matplotlib.pyplot as plt
from numpy import *
x = arange(0,2*pi,0.01)
y1 = sin(x)
y2 = cos(x)
plt.figure()
plt.plot(x,y1,color='r',linestyle='-',label='sin(x)')
plt.plot(x,y2,color='b',linestyle='-',label='cos(x)')
plt.legend()
plt.show()

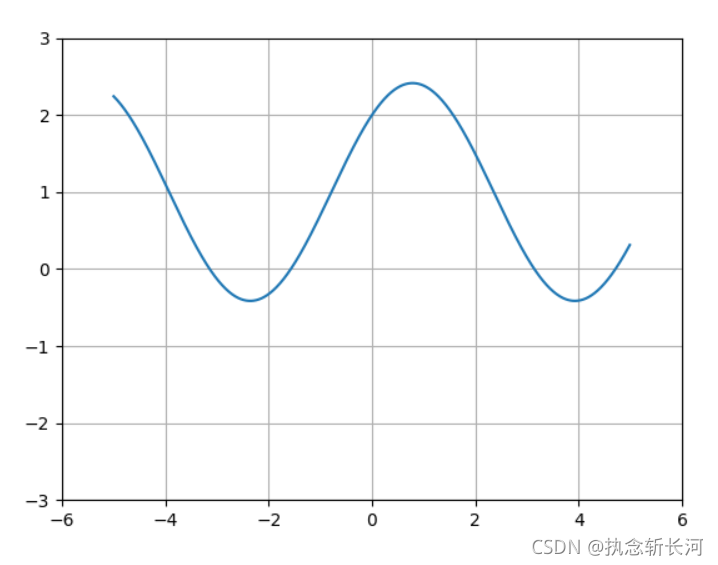
3.2 绘制以下函数的图像，判断其奇偶性，并观察其在x=0处的连续性

$(1)y=\sin x+\cos x+1$
$(2)y={\log }_2(x+\sqrt{1+x^2})$

import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-5,5,0.01)
y = np.sin(x) + np.cos(x) + 1
plt.figure()
plt.plot(x,y)
plt.axis([-6,6,-3,3])
plt.grid(True)
plt.show()