激活函数:只是一个抽象概念,使用激活函数时为了让中间输出多样化,能够处理更复杂的问题。
激活函数给神经元引入了非线性因素,若无激活函数,则每一层最后输出的都是上一层输入的线性函数,不管加多少层神经网络,我们最后的输出也只是最开始输入数据的线性组合而已。当加入多层神经网络时,就可以让神经网络拟合任何线性函数及非线性函数,从而使得神经网络可以适用于更多的非线性问题,而不仅仅是线性问题。
>> 01 sigmoid函数
????????
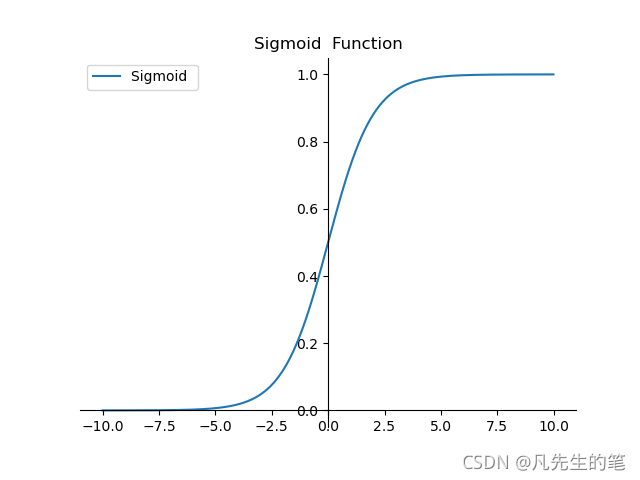
- ?sigmoid函数是机器学习中的一个比较常用的函数,用于隐层神经元输出,取值范围为(0,1);
- 它可以将一个实数映射到(0,1)的区间,用来做二分类,而且是单调递增,比较容易优化;
- 在特征相差比较复杂或是相差不是特别大时效果比较好;
- 优点:平滑、易于求导;
- 缺点:①收敛比较慢,反向传播求误差梯度时,求导涉及除法;②Sigmoid是软饱和,反向传播时,容易产生梯度消失,从而无法完成深层网络的训练;(当x趋于无穷大的时候,也会使导数趋于0)③Sigmoid函数并不是以(0,0)为中心点;?
from matplotlib import pyplot as plt
import numpy as np
import math
def sigmoid_function(x_list):
fx = []
for x in x_list:
# print(x)
fx.append(1 / (1 + np.exp(-x)))
return fx
if __name__ == '__main__':
x_list = np.arange(-10, 10, 0.01)
fx = sigmoid_function(x_list)
ax = plt.gca() # get current axis 获得坐标轴对象
ax.spines['right'].set_color('none') # 将右边的两条边颜色设置为空
ax.spines['top'].set_color('none') # 将上边的两条边颜色设置为空
ax.xaxis.set_ticks_position('bottom') # 指定下边的边为 x 轴
ax.yaxis.set_ticks_position('left') # 指定左边的边为 y 轴
ax.spines['bottom'].set_position(('data', 0)) # 指定的x轴绑定到0这个点
ax.spines['left'].set_position(('data', 0)) # 指定的y轴绑定到0这个点
plt.plot(x_list, fx, label='Sigmoid ', linestyle="-") # label为标签
plt.legend(['Sigmoid '])
plt.title('Sigmoid Function')
plt.show()??>> 02 tanh函数
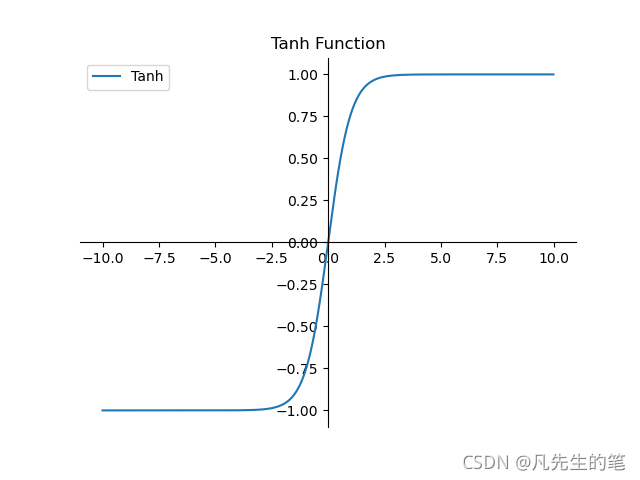
- 优点:①函数输出以(0,0)为中心;②收敛速度相对于Sigmoid更快;
- 缺点:tanh函数并没有解决sigmoid梯度消失的问题
from matplotlib import pyplot as plt
import numpy as np
import math
def tanh_function(x_list):
fx = []
for x in x_list:
fx.append((np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x)))
return fx
if __name__ == '__main__':
x_list = np.arange(-10, 10, 0.01)
fx = tanh_function(x_list)
ax = plt.gca() # get current axis 获得坐标轴对象
ax.spines['right'].set_color('none') # 将右边的两条边颜色设置为空
ax.spines['top'].set_color('none') # 将上边的两条边颜色设置为空
ax.xaxis.set_ticks_position('bottom') # 指定下边的边为 x 轴
ax.yaxis.set_ticks_position('left') # 指定左边的边为 y 轴
ax.spines['bottom'].set_position(('data', 0)) # 指定的x轴绑定到0这个点
ax.spines['left'].set_position(('data', 0)) # 指定的y轴绑定到0这个点
plt.plot(x_list, fx, label='Tanh', linestyle="-") # label为标签
plt.legend(['Tanh'])
plt.title('Tanh Function')
plt.show()?>> 03 tanh函数
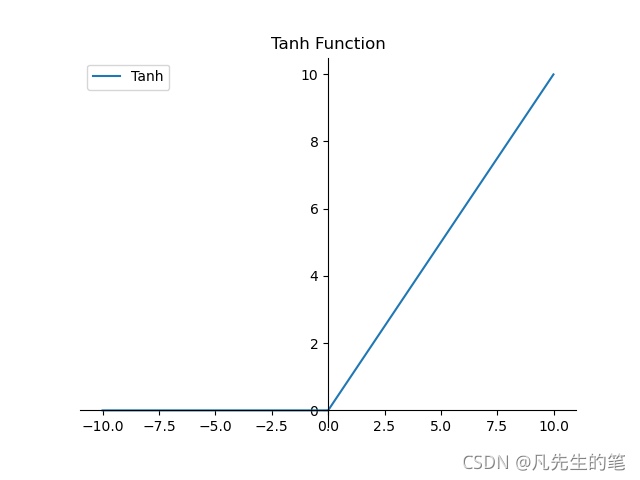
- 优点:①收敛速度快;②有效的缓解了梯度消失问题;③对神经网络可以使用稀疏表达;④对于无监督学习,也能获得很好的效果。
- 缺点:在训练过程中容易出现神经元失望,之后梯度永远为0的情况。
from matplotlib import pyplot as plt
import numpy as np
import math
def sigmoid_function(x_list):
fx = []
for x in x_list:
fx.append(np.where(x < 0, 0, x))
return fx
if __name__ == '__main__':
x_list = np.arange(-10, 10, 0.01)
fx = sigmoid_function(x_list)
print(len(fx))
ax = plt.gca() # get current axis 获得坐标轴对象
ax.spines['right'].set_color('none') # 将右边的两条边颜色设置为空
ax.spines['top'].set_color('none') # 将上边的两条边颜色设置为空
ax.xaxis.set_ticks_position('bottom') # 指定下边的边为 x 轴
ax.yaxis.set_ticks_position('left') # 指定左边的边为 y 轴
ax.spines['bottom'].set_position(('data', 0)) # 指定的x轴绑定到0这个点
ax.spines['left'].set_position(('data', 0)) # 指定的y轴绑定到0这个点
plt.plot(x_list, fx, label='Tanh', linestyle="-") # label为标签
plt.legend(['Tanh'])
plt.title('Tanh Function')
plt.show()?
??