[人工智能]一篇实验结果统计检验入门文档

一篇统计基础文档

写在前面

以前看到保哥发教程发写的文档就觉得很没有必要，感觉高端的统计学知识、争论离我们的需求很远，而基础的统计学应用早就看腻了。

直到最近王行同学拿到实验数据想做统计却根本不知道统计是什么的时候，我感受到了保哥的无奈，他真滴想让大家知道真正的统计是怎样的。

我打算用保哥的风格写一篇我们神经科学/工程入门的统计检验应用的文档，有2个目的：让王行学习、作为自己的第一篇CSDN博客。

有可能有些理解不是很正确，但是应该够用。

2021.10.21 21:50

正文

正态分布

感觉需要明确一下正态分布

又名高斯分布，这些都听不出什么，但是从英文名可以得到他最直观的解释：Normal Distribution。

我们可以从生活中的各项指标中得到Notmal distribution的特征：中间高，两头低。比如考试成绩：大多数人都会考70-90分之间，少数人会考90分以上或者70分一下，那么成绩分布图大概就是下图的形状，这个形状就是正态分布

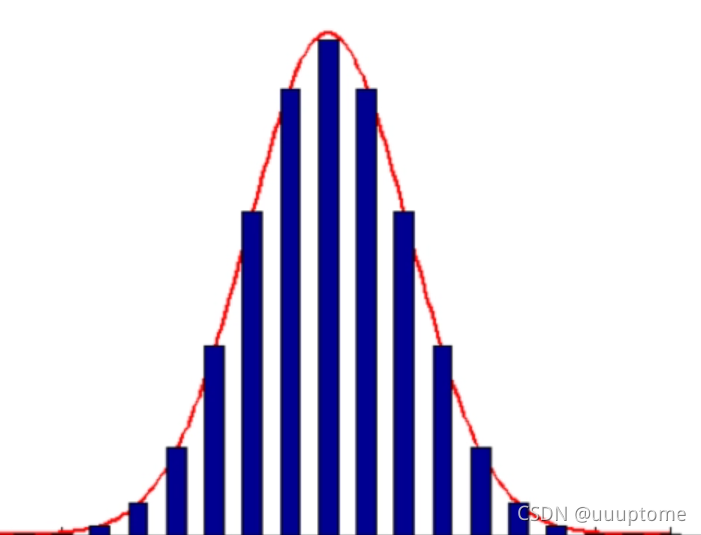
这里我们就可以写考试成绩X服从正态分布N（均值，方差），均值就是平均成绩，方差代表了大家成绩的集中程度，大家都考的差不多，方差就小；大家成绩差距大，方差就大。($X$~$N(\mu ,{\sigma }^2)$)

为什么要做统计检验

许多人（这里特指王行）不知道做统计检验的目的是什么，只是觉得在文献中看到了别人的工作两个柱状图之间加了个星号后似乎说服力大了许多，因此也想做一下检验，这是非常气人的。

我们采集、收集到的实验数据，是一组样本，是在一个总体中随机取样得到的，样本并不能直接指代总体。

比如人一整天每时每刻的体重是一个总体，这个总体可能是服从正态分布的。如果你每次都在我吃完饭后的时间对我的体重进行取样，以此估计我的体重，那么很容易把我的体重估计的偏大。因为你的样本大概率都是来自上面分布图的右侧。

同样的，如果连续三天在我吃完中饭采集体重，分别是（101Kg，100Kg，99Kg），在王行吃中饭前采集体重（46Kg，45Kg，44Kg），这时候得出结论，我的体重比王行大，这我是肯定不服气的，因为样本并不能完全代表整体，或许我吃饭前是非常轻的，但并没有采集到我吃饭前的体重。因此这时候就需要统计检验来告诉我们，有多大的把握说明，我比王行的体重大。

类比到实验中，如果采集了5只老鼠打药前后分别大脑的脑电，计算了30-80Hz频带的能量，直接对比五只老鼠打药前平均能量和打药后的平均能量，发现打药后能量增加了，由此得出结论：打药能使能量增加。这并没有足够的说服力，因为你想得出的结论是所有的老鼠打药后能量都会增加，而你的样本只能提供的信息是这五只老鼠打药后平均能量增加，这时候，需要一个统计检验的结果，告诉你，基于现有的数据，你有多大把握告诉大家，打药会对老鼠脑电的能量有影响。

假设检验

检验一般有一个零假设$H_0$，然后通过统计量和遵循的分布得到，在现有数据的基础上能不能拒绝$H_0$

在我们的实际应用，一般假设的$H_0$是 $mea{n}_{pre}=mea{n}_{post}$，意思是假设前后数据的均值并没有改变，检验的结果一般是一个p值，这个p值可以理解为：在零假设下，获得现有样本结果甚至更差的结果的概率

（我知道p值的定义真滴很难正确解释，保哥至少发过2篇关于p值定义、p值意义的paper，但是我觉得上述定义是能够理解的，而且这个理解并不特别错误）

还是上面这个例子，一共5只老鼠，打药前能量是（10，11，12，13，15），打药后能量是（14，16，17，18，19）统计检验做的零假设是打药前后能量的均值并没有改变，计算得到的p值是$p<0.001$，意思是有小于0.001的概率在前后能量均值不改变下，能够观测到当前样本，也就是说均值大概率是改变了的，否则不可能有这样的结果。一般p值的界限卡在0.05、0.01、0.005等不同水平。

介绍几种最常用的统计检验方法和应用场景

One sample T test

从标题上也可以听得出来，只有一组样本，只有一组样本的时候怎么对比的？答案是跟一个定值比（经常是经过变换后和0比）。

比如Y和X有一个关系k，即Y~kX（相关的符号我不会打），经过多组样本算出了多个k，如果Y和X真的有关系，那么这个k肯定是不为0的（为0代表没有关系），我们就拿这多个样本k进行检验，看有多大的把握说真实的K不为0。

用仿真数据试一下：

假设XY其实没有关系，K服从均值为0，方差为1的正态分布，我们随机取样10个值作为样本

k=normrnd(0,1,[10,1])// 0均值 方差1 产生10*1的数据

可以看到，随机取样的K均值有0.62，但是我们并不能说真实的K不等于0，因为统计检验的结果显示p=0.294,没有足够的把握拒绝K=0的零假设

Paired T test

适用情况：两组数据是两两配对的

比如10只老鼠每次打药前后各10个观测数据，每只老鼠打药前后的两个数据是配对的，是有一定关系的，这时候要用配对t检验。这里零假设就是打药前后能量均值没有改变。

仿真：

pre=normrnd(10,1,[10,1]) % 打药前老鼠的能量服从均值为10方差为1的正态分布
delta=normrnd(1,2,[10,1]) % 真的存在变化，变化量服从均值为1方差为2的正态分布
post=pre+delta % 打药后 = 打药前 + 变化量

第一行数据随机采样了10只老鼠的初始能量，假设真的存在变化，随机采样了均值为1方差为2的变化量，两者相加得到打药后的能量，通过配对t检验，p=0.021<0.05，说明两组均值有显著变化，打药后能量显著增加了（即使有的样本打药后观测的能量降低了，比如样本2，但是统计检验的结果显示有很大把握说明均值是变化了的）。

如果把上面的代码变一下，变化量均值改为0：

pre=normrnd(10,1,[10,1]) % 打药前老鼠的能量服从均值为10方差为1的正态分布
delta=normrnd(0,2,[10,1]) % 真的存在变化，变化量服从均值为0方差为2的正态分布
post=pre+delta % 打药后 = 打药前 + 变化量```

可以看到，p=0.545，不能说明打药前后真实均值发生了变化

从上面两组仿真可以看到，统计检验真的可以帮助我们从我们的数据中得到一些真实的结论

independent T test

独立样本检验，和配对样本检验相对应，在两组样本没有相关性的时候使用。比如对比一组男生和一组女生的身高差异用独立样本检验，对比一组女生10年前和今天身高的差异用配对样本检验

零假设依旧是两组均值相等

仿真

假设对比一下一组抑郁的老鼠和一组没有抑郁的老鼠的脑电能量有没有差异：

Group1=normrnd(10,1,[10,1]) %第一组老鼠的能量服从均值为10 方差为1的正态分布
Group2=normrnd(12,1,[10,1]) %第二组老鼠的能量服从均值为12 方差为1的正态分布

可以看到，P<0.001，说明抑郁组和正常组的大脑能量有显著差异

ANOVA

前面介绍的都是一组（one sample t-test）、和两组之间（paired or independent t-test）的检验方法，有可能相对比多组之间的比较，这时候就需要方差分析了

比如想看一下一年级、二年级、三年级三个年级学生的身高有没有显著差异，就要做方差分析，基本做法和前面介绍的类似，这里就不仿真了。

方差分析得到p值显著，只能说明组间有差异，不能得到哪些组有差异，比如：上述的对比p=0.01，说明三个年级的学生身高确实有差异，但是你不知道差异到底来自于哪些年级之间，因此这时候需要post hoc 即事后多重比较，对三个年级的结果进行两两的独立样本t检验，找到真正的差异来源，方差分析只能做一个多组之间初步的判断。

进阶

前面介绍的都是最最简单基础的统计知识，只能完成一部分应用场景，在实际的分析中，由于复杂的实验设计，往往需要更加复杂的统计检验流程，这里不详述了，用到可以自行查阅

举一些例子：

• 如果有两组老鼠，一组老鼠打药，一组老鼠打生理盐水，分别采集两组数据（共四组，2组的处理方式*2个时间点），这时候有两个因素：处理方式、时间，前面介绍的单因素的分析就不适用了，可能要做双因素方差分析或repeated measure（因为没做过所以不是特别明确，停留在保哥的课堂）
• 如果你采集了多个时间点，比如刺激后5min, 10min, 15min, 20min,四组，可能使用方差分析也不是很好，因为方差分析是把这四组当成了完全独立的组，在统计分析的时候抛弃了时间这一有效的信息（4组的组号是能提供一些信息的，但是方差分析没有考虑到）。这时候用线性模型比较好？
• 还有，上述的t检验、anova都是参数方法，对数据的分布有一定要求（自查），如果是不满足要求，需要用对应的非参数方法（自查）

假阳性和矫正

假阳性: false positive 说的是零假设成立，但是拒绝了零假设的情况。

比如：零假设是我昨天的体重和今天的体重相等，但是采样的时候，昨天采样了3次都是饭前，今天采样的3次都是饭后，通过检验发现p=0.001，得出结论昨天今天体重不等，这就是假阳性。

上面的例子比较绝对，在实际的实验中，因为我们是随机取样，一般不会出现上述这种情况，但是还是有一定概率（p=0.05, 所以我们认为就是5%），真的出现了这种情况（真的就这么巧，昨天三次通知体测的时间都在饭前，今天三次通知体测的时间都在饭后），假阳性就出现了。但是因为概率真的很低，只有5%，我们还是大胆的认为我们的结论是正确的。

但是！

上面是只有一次比较的时候，如果有多次比较，假阳性概率就大大增加了

比如我们采集了32通道的脑电，对比两天我们脑电能量的差异，按理说我们两天没有啥重大疾病出现的话，每个通道的能量应该没有显著性差异。我们做了32次检验，每次检验犯错（出现假阳性）概率为5%，那么32次实验出现假阳性的概率是$1?(1?5\%{)}^{32}=80.6\%$，也就是说大概率会出现假阳性！

这时候我们对比了32次，发现枕叶的一个通道能量昨天今天有差异，就得出结论今天是不是用眼过度了，枕叶能量都变化了，这个结论是不可靠的

这时候我们就需要矫正，矫正的方法就是提高显著性的阈值，我们做一次实验，p<0.05就可以认为显著，做10次实验，为了避免假阳性，可能p<0.005我们才能认为显著

最后

上面的介绍为了通俗易懂，可能有些论述是错误的，毕竟统计是非常严谨的领域。

生成随机数据用的matlab，统计分析用的jamovi，强推jamovi，图表都非常好看和规范，直接可以用到论文里的那种，本来想趁机学一下R语言，但是由于太懒，没有去试。

今天先写到这吧，在保哥的熏陶下，其实还知道很多统计知识，但是写起来太费劲了，如果还有问题，博资考后再加上去。