使用两层网络实现手写数字识别(《深度学习入门:基于Python的理论与实现》实践笔记)
一、加载mnist数据集
这部分可以看看本人写的另一篇文章:将MNIST手写数字数据集导入NumPy数组。
二、构建两层网络
1. 两层网络结构
两层网络的结构图如下所示:
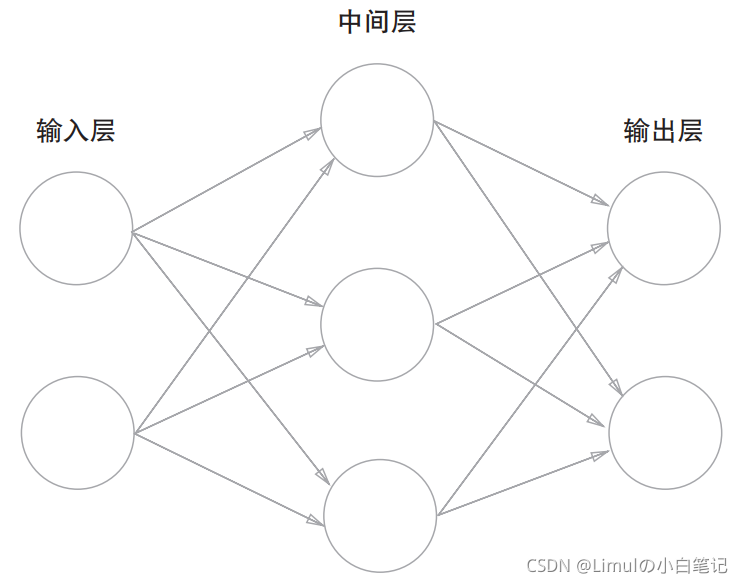
- 由于mnist手写数字的图片都是单通道28×28像素的图片,在将图片所有像素一维展开后得到784个像素,所以输入层一共784个神经元。
- 中间层的神经元个数可自己设定,这里就直接使用书中例子的50个神经元。
- 由于这个神经网络最后需要告诉我们这个图片是哪个数字,那么结果就可能为0~9这10个数字,所以输出层的神经元个数为10。
2. 参数
- 参数一共有4个:第一层权重w1,第一层偏置值b1,第二层权重w2,第二层偏置值b2。
- 由于两层都是全连接层,所以权重w1是784(输入层神经元个数)×50(隐藏层神经元个数)的数组,而权重w2是50(隐藏层神经元个数)×10(输出层神经元个数)的数组。
- 偏置值b1为50(隐藏层神经元个数),b2为10(输出层神经元个数)。
- 参数在构建网络之初就初始化。初始化时,权重w随机初始化,偏置值b初始化为0。
# 初始化权重
self.params = {
'W1': weight_init_std * np.random.randn(input_size, hidden_size),
'b1': np.zeros(hidden_size),
'W2': weight_init_std * np.random.randn(hidden_size, output_size),
'b2': np.zeros(output_size)
}
3. 信号传递
- 网络的第一层是全连接层,然后信号经过sigmoid激活函数后进入第二层全连接层,最后经过softmax归一化层得到输出。
def predict(self, x):
w1, w2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, w1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, w2) + b2
y = softmax(a2)
return y
4. 计算梯度
- 神经网络在训练的时候需要向前传递信号,然后反向传递计算梯度更新参数,所以在网络的定义中要提供计算梯度的函数。
def gradient(self, x, t):
w1, w2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, w1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, w2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, w2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
5. 计算精准度
- 最后体现训练结果的是网络的精准度,就是将输入放入网络,然后对比网络的输出和监督数据,计算这个网络的正确率。
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
三、训练模型
- 在构建好模型后,就可以开始训练了。训练模型就是将数据导入模型,然后向前传播,然后计算梯度并更新参数,然后再进行下一轮的训练。
- 为了反映这个训练情况,每完成一定次数的训练,要输出当前模型的准确度。
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
# 生成网络
if os.path.exists('model.pkl'):
with open('model.pkl', 'rb') as fp:
network = pickle.load(fp)
else:
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iter_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iter_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 梯度
grad = network.gradient(x_batch, t_batch)
# 更新
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print(train_acc, test_acc)
# 保存模型,下次训练时不必从头训练
with open('model.pkl', 'wb') as fp:
pickle.dump(network, fp, -1)
四、完整代码
构建并训练模型的完整代码如下所示:
import numpy as np
import urllib.request
import gzip
import os
import pickle
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 溢出对策
return np.exp(x) / np.sum(np.exp(x))
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 监督数据是one-hot-vector的情况下,转换为正确解标签的索引
if t.size == y.size:
t = t.argmax(axis=1)
y_batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / y_batch_size
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
x_grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
x_grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 还原值
it.iternext()
return x_grad
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 初始化权重
self.params = {
'W1': weight_init_std * np.random.randn(input_size, hidden_size),
'b1': np.zeros(hidden_size),
'W2': weight_init_std * np.random.randn(hidden_size, output_size),
'b2': np.zeros(output_size)
}
def predict(self, x):
w1, w2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, w1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, w2) + b2
y = softmax(a2)
return y
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x:输入数据, t:监督数据
def numerical_gradient(self, x, t):
def loss_w(): return self.loss(x, t)
grads = {
'W1': numerical_gradient(loss_w, self.params['W1']),
'b1': numerical_gradient(loss_w, self.params['b1']),
'W2': numerical_gradient(loss_w, self.params['W2']),
'b2': numerical_gradient(loss_w, self.params['b2'])
}
return grads
def gradient(self, x, t):
w1, w2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, w1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, w2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, w2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
def load_mnist(normalize=True, flatten=True, one_hot_label=False):
# 用dataset字典保存由4个文件读取得到的np数组
dataset = {}
# 若不存在pkl文件,下载文件导入numpy数组,并生成pkl文件
if not os.path.exists('mnist.pkl'):
# MNIST数据集的4个文件
key_file = {
'train_img': 'train-images-idx3-ubyte.gz', 'train_label': 'train-labels-idx1-ubyte.gz',
'test_img': 't10k-images-idx3-ubyte.gz', 'test_label': 't10k-labels-idx1-ubyte.gz'
}
# 下载文件并导入numpy数组
for _ in key_file.keys():
print('Downloading ' + key_file[_] + '...')
urllib.request.urlretrieve('http://yann.lecun.com/exdb/mnist/' + key_file[_], key_file[_]) # 下载文件
print('Download finished!')
# 用二进制只读方式打开.gz文件
with gzip.open(key_file[_], 'rb') as f:
# img文件前16个字节不是img数据,跳过读取;label文件前8个不是label数据,跳过读取
dataset[_] = np.frombuffer(f.read(), np.uint8,
offset=16 if _ == 'train_img' or _ == 'test_img' else 8)
if _ == 'train_img' or _ == 'test_img':
dataset[_] = dataset[_].reshape(-1, 1, 28, 28)
# 生成mnist.pkl
print('Creating pickle file ...')
with open('mnist.pkl', 'wb') as f:
pickle.dump(dataset, f, -1)
print('Create finished!')
# 若存在pkl文件,把pkl文件内容导入numpy数组
else:
with open('mnist.pkl', 'rb') as f:
dataset = pickle.load(f)
# 标准化处理
if normalize:
for _ in ('train_img', 'test_img'):
dataset[_] = dataset[_].astype(np.float32) / 255.0
# one_hot_label处理
if one_hot_label:
for _ in ('train_label', 'test_label'):
t = np.zeros((dataset[_].size, 10))
for idx, row in enumerate(t):
row[dataset[_][idx]] = 1
dataset[_] = t
# 展平处理
if flatten:
for _ in ('train_img', 'test_img'):
dataset[_] = dataset[_].reshape(-1, 784)
# 返回np数组
return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])
if __name__ == '__main__':
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
# 生成网络
if os.path.exists('model.pkl'):
with open('model.pkl', 'rb') as fp:
network = pickle.load(fp)
else:
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iter_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iter_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 梯度
# grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# 更新
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print(train_acc, test_acc)
# 保存模型,下次训练时不必从头训练
with open('model.pkl', 'wb') as fp:
pickle.dump(network, fp, -1)
结果截图如下所示:
完整的pycharm工程文件可查看:TrainNeuralnet.rar
本实例来自于,由[日]斋藤康毅所著的《深度学习入门:基于Python的理论与实现》。