KNN算法的原理
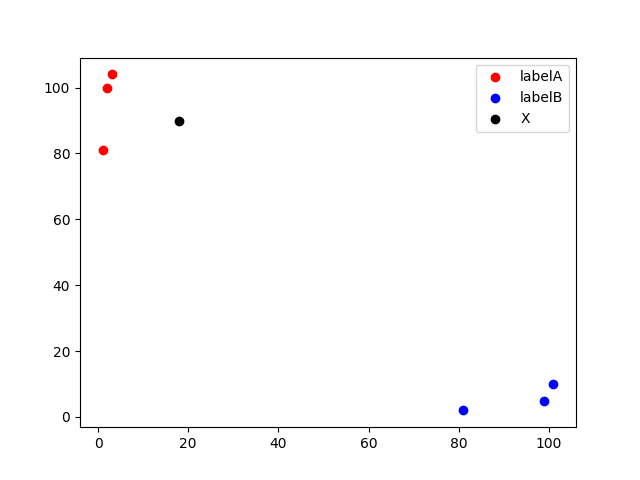
原理:K近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例(也就是该实例的K个邻居), 这K个实例的多数属于某个类,就把该输入实例分类到这个类中。(这类似于现实生活中少数服从多数的思想)如下图所示,当k=3时,黑点最邻近的3个实例中有2个是红点,而红点属于labelA,故此时黑点应当属于labelA。

注:k近邻的k值选取是关键,因为k值过小,将意味着我们的整体模型会变得复杂,容易发生过拟合;k值过大就会使得邻域过大,过大的邻域内包含着与输入实例较远的(也就是不相似的)训练实例也会对预测起作用,使预测发生错误。故k值选取很重要的关键是实验调参。
方法:我们知道了原理,而我们是如何计算新的输入实例的邻近实例呢?这时我们就用到了欧氏距离:
d
i
s
(
x
,
y
)
=
∑
i
=
1
n
(
x
i
?
y
i
)
2
dis(x,y)=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}
dis(x,y)=i=1∑n?(xi??yi?)2?
如在二维空间中,A点坐标(x,y),B点坐标(x1,y1),故两点间的距离为
d
i
s
(
x
,
y
)
=
(
x
1
?
x
)
2
+
(
y
1
?
y
)
2
dis(x,y)=\sqrt{(x_1-x)^2+(y_1-y)^2}
dis(x,y)=(x1??x)2+(y1??y)2?
在三维空间中,A点坐标(x,y,z),B点坐标(x1,y1,z1),故两点间的距离为
d
i
s
(
x
,
y
)
=
(
x
1
?
x
)
2
+
(
y
1
?
y
)
2
+
(
z
1
?
z
)
2
dis(x,y)=\sqrt{(x_1-x)^2+(y_1-y)^2+(z_1-z)^2}
dis(x,y)=(x1??x)2+(y1??y)2+(z1??z)2?
由此我们可以推导出n维空间的距离,即若A点坐标(x1,x2,……xn),B点坐标(y1,y2,……yn),则两点之间的距离为
d
i
s
(
x
,
y
)
=
(
x
1
?
y
1
)
2
+
(
x
2
?
y
2
)
2
+
?
+
(
x
n
?
y
n
)
=
∑
i
=
1
n
(
x
i
?
y
i
)
2
dis(x,y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots+(x_n-y_n)}=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}
dis(x,y)=(x1??y1?)2+(x2??y2?)2+?+(xn??yn?)?=i=1∑n?(xi??yi?)2?
KNN算法的实现
以下图中的数据为例
带注释运行结果版,下滑可看无注释运行结果版
import numpy as np
import operator
#已知分类的数据
x_data = np.array([[3, 104],
[2, 100],
[1, 81],
[101, 10],
[99, 5],
[81, 2]])
y_data = np.array(['A', 'A', 'A', 'B', 'B', 'B'])
x_test = np.array([18, 90])
#计算样本数量
x_data_size = x_data.shape[0] #shape(0)查询有多少行
'''
复制x_test
np.tile(x_test, (x_data_size, 1))
其中的(x_data_size, 1)是将x_test行复制x_data_size次,列复制1次
若np.tile(x_test, (1, 1))
结果为
[[18 90]]
若np.tile(x_test, (2, 2))
结果为
[[18 90 18 90]
[18 90 18 90]]
'''
#下面五步就是使用欧氏距离求邻近实例
#1、计算x_test与每一个样本的差值
diffMat = np.tile(x_test, (x_data_size, 1)) - x_data
'''
print(diffMat)
[[ 15 -14]
[ 16 -10]
[ 17 9]
[-83 80]
[-81 85]
[-63 88]]
'''
#2、计算差值的平方
sqDiffMat = diffMat**2
'''
print(sqDiffMat)
[[ 225 196]
[ 256 100]
[ 289 81]
[6889 6400]
[6561 7225]
[3969 7744]]
'''
#3、求和,求得每一行的和
sqDiffMat = sqDiffMat.sum(axis=1)
'''
print(sqDiffMat)
[ 421 356 370 13289 13786 11713]
'''
#5、开方
distances = sqDiffMat**0.5
'''
print(distances)
[ 20.51828453 18.86796226 19.23538406 115.27792503 117.41379817 108.2266141 ]
'''
#从小到大排序
#argsort返回的是索引
sortedDistances = distances.argsort()
'''
print(sortedDistances)
[1 2 0 5 3 4]
'''
classCount = {}
#设置k
k = 5
for i in range(k):
#获取标签
votelabel = y_data[sortedDistances[i]]
#统计标签数量
#字典的get方法,(a,0)若字典中有键a,则返回a的值,若无则返回规定值0
classCount[votelabel] = classCount.get(votelabel, 0) + 1
#根据operator.itemgetter(1)-第1个值d对classCount排序,然后再取倒序
sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse=True)
#获取数量最多的标签
knnclass = sortedClassCount[0][0]
print(knnclass)
简洁版
import numpy as np
import operator
#已知分类的数据
x_data = np.array([[3, 104],
[2, 100],
[1, 81],
[101, 10],
[99, 5],
[81, 2]])
y_data = np.array(['A', 'A', 'A', 'B', 'B', 'B'])
x_test = np.array([18, 90])
#计算样本数量
x_data_size = x_data.shape[0] #shape(0)查询有多少行
#复制x_test
#print(np.tile(x_test, (x_data_size, 1)).shape)
#计算x_test与每一个样本的差值
diffMat = np.tile(x_test, (x_data_size, 1)) - x_data
#计算差值的平方
sqDiffMat = diffMat**2
#求和
sqDiffMat = sqDiffMat.sum(axis=1)
#开方
distances = sqDiffMat**0.5
#从小到大排序
sortedDistances = distances.argsort()
classCount = {}
#设置k
k = 5
for i in range(k):
#获取标签
votelabel = y_data[sortedDistances[i]]
#统计标签数量
classCount[votelabel] = classCount.get(votelabel, 0) + 1
#根据operator.itemgetter(1)-第1个值d对classCount排序,然后再取倒序
sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse=True)
#获取数量最多的标签
knnclass = sortedClassCount[0][0]
print(knnclass)