多元线性回归之预测房价
一、多元线性回归
在回归分析中,如果
有两个或两个以上的自变量,就称为多元回归。事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。因此多元线性回归比一元线性回归的实用意义更大。
回归系数:

线性回归数学模型:
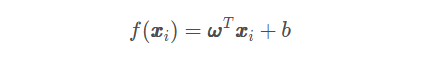
1. 理论基础
- 一元线性回归分析的数学模型为:y = a+bx+ε。
- 使用偏差平方和分别对参数a和参数b求偏导,可以得到线性模型的未知参数a、b的最小二乘估计值,其中,偏差平方和定义为∑(yi-a-bXi)2
二、案例分析
- 对未来房价进行预测,在一定程度上影响着社会经济的发展。房屋售价与多因素有关,并且房屋价格与影响房价的一些因素存在线性关系,所以选取多元线性回归模型研究该问题较为合适。
- 本次课题研究通过对某段时间某地区的已售房价数据进行线性回归分析,探索
街区(neighborhood),房屋面积(area),卧室数bedrooms,浴室数bathrooms,房屋风格(style)与 房价(price)等因素,并对这些影响因素的影响程度进行分析,利用分析得到的数据,对未来房价的趋势和走向进行预测。
三、数据预处理
1. 错误数据清洗
- 原始数据中,
存在卧室,浴室或者房屋面积等数据不合理的情况,需要对数据进行清洗操作
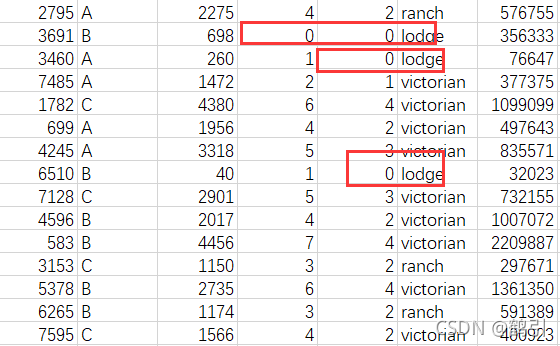
- 数据->筛选
自定义数据进行筛选操作
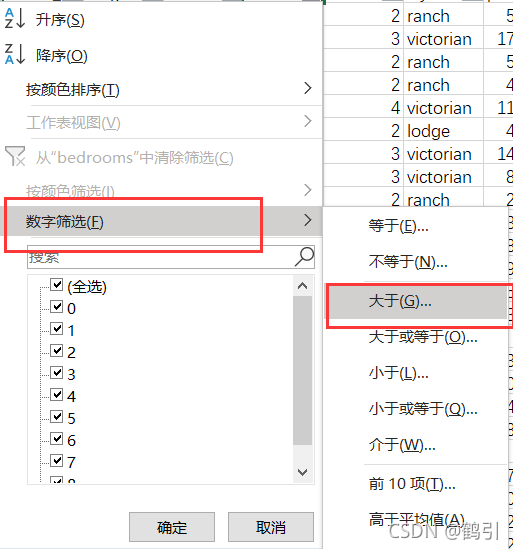

- 重复上述操作将异常数据清理掉
bathrooms
- 清洗操作完成
- 数据->筛选
2. 非数值型数据转化
在原始数据中,存在非数值型数据,需要进行转化
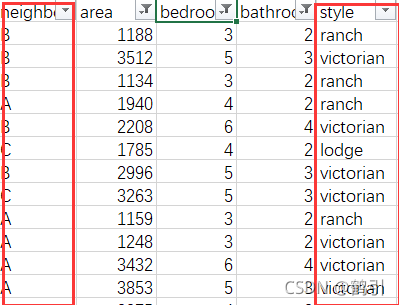
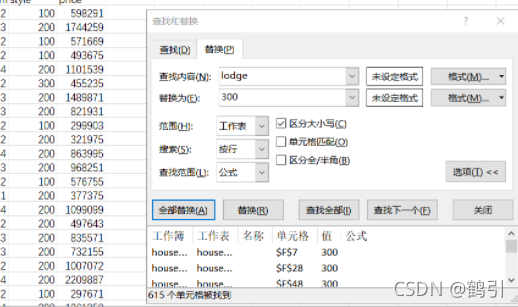
neighborhoodA,B,C转化为1,2,3
四、使用Excel
1. 实现
-
删除表格中的非数据项,进行后续的数据线性回归
-
勾选
数据分析中的线性回归
若没出现数据分析项- 选择更多里的选项
- 加载项->转到
- 勾选分析库
- 选择更多里的选项
-
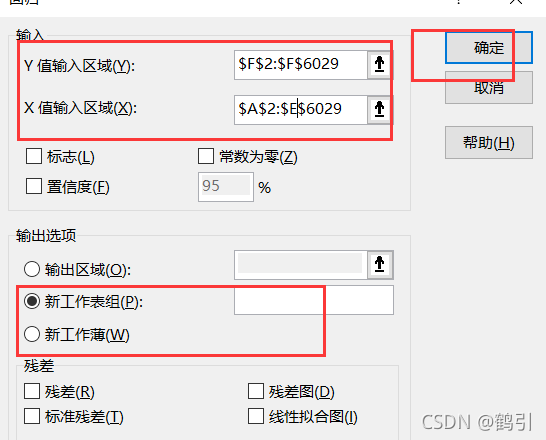
设置
输入和输出选项
-
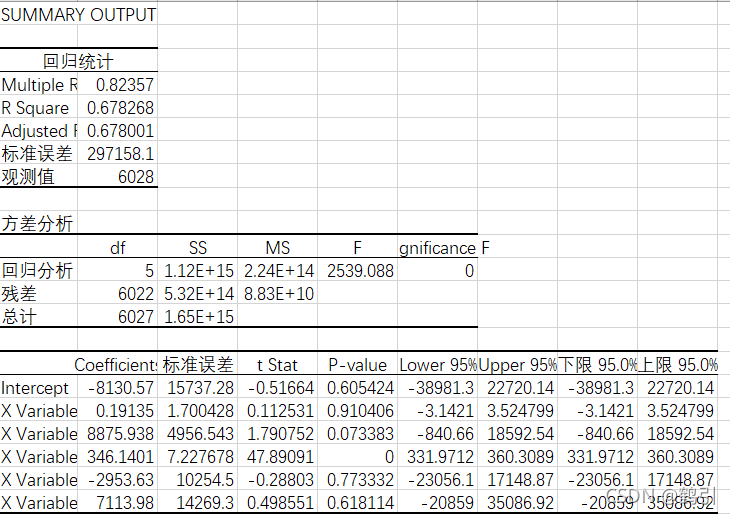
输出结果
2. 分析
-
Multiple R:相关系数R = 0.82357, x,y相关度高 -
R Square:决定系数R2
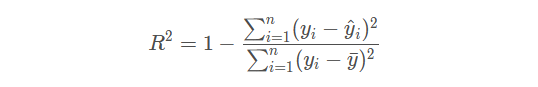
本数据集回归分析R2 = 0.678001 说明自变量能解释因变量范围大概在67.8% -
子表

- X Variable 1 : house_id
- X Variable 2 : neighborhood
- X Variable 3 : area
- X Variable 4 : bedrooms
- X Variable 5 : bathrooms
-
根据
Coefficients推算估计方程
? y = 0.19135 x 1 + 8875.938 x 2 + 346.1401 x 3 ? 2953.63 x 4 + 7113.98 x 5 \ y = 0.19135x_1 + 8875.938x_2 + 346.1401x_3 - 2953.63x_4 + 7113.98x_5 ?y=0.19135x1?+8875.938x2?+346.1401x3??2953.63x4?+7113.98x5? -
P-value
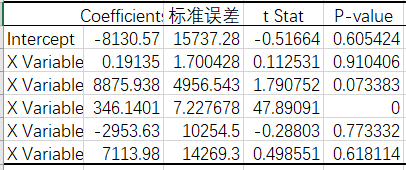
- 自变量房屋面积 ? x 2 \ x_2 ?x2?的P值远小于显著性水平0,因此房屋面积(area)与房价(price)相关
bedrooms和bathrooms,house_id的P值远大于显著性水平0.05与房价相关性较弱,甚至不存在相关性关系
五、代码方式实现多元线性回归
1. 数据预处理
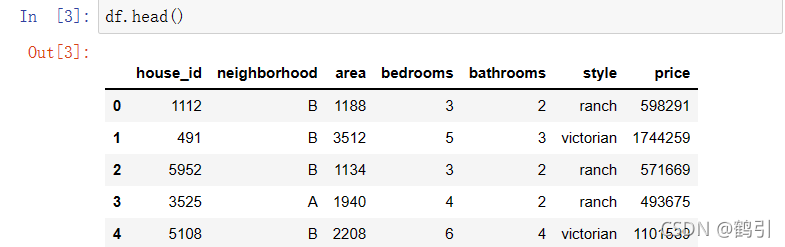
- 查看数据基础信息
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt#导入数据
df = pd.read_csv("E:\人工智能\house_prices1.csv")
#读取数据的基础信息
df.info()

- 冗余数据
# 判断数据中是否存在重复观测
df.duplicated().any()

# 判断各变量中是否存在缺失值
df.isnull().any(axis = 0)
# 各变量中缺失值的数量
df.isnull().sum(axis = 0)
# 各变量中缺失值的比例
df.isnull().sum(axis = 0)/df.shape[0]
- 异常数据值识别处理
# 异常值处理
# ================ 异常值检验函数:iqr & z分数 两种方法 =========================
def outlier_test(data, column, method=None, z=2):
""" 以某列为依据,使用 上下截断点法 检测异常值(索引) """
"""
full_data: 完整数据
column: full_data 中的指定行,格式 'x' 带引号
return 可选; outlier: 异常值数据框
upper: 上截断点; lower: 下截断点
method:检验异常值的方法(可选, 默认的 None 为上下截断点法),
选 Z 方法时,Z 默认为 2
"""
# ================== 上下截断点法检验异常值 ==============================
if method == None:
print(f'以 {column} 列为依据,使用 上下截断点法(iqr) 检测异常值...')
print('=' * 70)
# 四分位点;这里调用函数会存在异常
column_iqr = np.quantile(data[column], 0.75) - np.quantile(data[column], 0.25)
# 1,3 分位数
(q1, q3) = np.quantile(data[column], 0.25), np.quantile(data[column], 0.75)
# 计算上下截断点
upper, lower = (q3 + 1.5 * column_iqr), (q1 - 1.5 * column_iqr)
# 检测异常值
outlier = data[(data[column] <= lower) | (data[column] >= upper)]
print(f'第一分位数: {q1}, 第三分位数:{q3}, 四分位极差:{column_iqr}')
print(f"上截断点:{upper}, 下截断点:{lower}")
return outlier, upper, lower
# ===================== Z 分数检验异常值 ==========================
if method == 'z':
""" 以某列为依据,传入数据与希望分段的 z 分数点,返回异常值索引与所在数据框 """
"""
params
data: 完整数据
column: 指定的检测列
z: Z分位数, 默认为2,根据 z分数-正态曲线表,可知取左右两端的 2%,
根据您 z 分数的正负设置。也可以任意更改,知道任意顶端百分比的数据集合
"""
print(f'以 {column} 列为依据,使用 Z 分数法,z 分位数取 {z} 来检测异常值...')
print('=' * 70)
# 计算两个 Z 分数的数值点
mean, std = np.mean(data[column]), np.std(data[column])
upper, lower = (mean + z * std), (mean - z * std)
print(f"取 {z} 个 Z分数:大于 {upper} 或小于 {lower} 的即可被视为异常值。")
print('=' * 70)
# 检测异常值
outlier = data[(data[column] <= lower) | (data[column] >= upper)]
return outlier, upper, lower
- 进行异常值检测
#对数据进行异常值检测
outlier, upper, lower = outlier_test(data=df, column='price', method='z')
outlier.info();
outlier.sample(5)
- 丢弃异常值
# 这里简单的丢弃即可
df.drop(index=outlier.index, inplace=True)
- 统计非数值变量
# 类别变量,又称为名义变量,nominal variables
nominal_vars = ['neighborhood', 'style']
for each in nominal_vars:
print(each, ':')
print(df[each].agg(['value_counts']).T)
# 直接 .value_counts().T 无法实现下面的效果
## 必须得 agg,而且里面的中括号 [] 也不能少
print('='*35)
# 发现各类别的数量也都还可以,为下面的方差分析做准备

- 绘制热力图
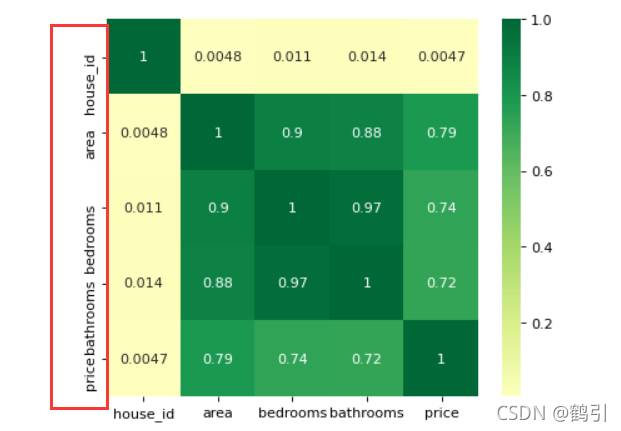
通过热力图可以看出area,bedrooms,bathrooms变量与房屋价格 price 的关系都还比较强,放入模型,但分类变量 style与 neighborhood两者与price的关系未知。
- 方差分析
刚才的探索我们发现,style 与 neighborhood的类别都是三类,如果只是两类的话我们可以进行卡方检验,所以这里我们使用方差分析
# 利用回归模型中的方差分析
## 只有 statsmodels 有方差分析库
## 从线性回归结果中提取方差分析结果
import statsmodels.api as sm
from statsmodels.formula.api import ols # ols 为建立线性回归模型的统计学库
from statsmodels.stats.anova import anova_lm
- 样本量和置信水平 α_level 的注意点(置信水平 α 的选择经验)
样本量 ??????? α-level
≤ 100 ??????? 10%
100 < n ≤ 500????5%
500 < n ≤ 1000???1%
n > 2000 ??????千分之一- 样本量过大,α-level 就没什么意义了。
- 数据量很大时,p 值就没用了,样本量通常不超过 5000,
- 为了证明两变量间的关系是稳定的,样本量要控制好。
# 从数据集样本中随机选择 600 条,如果希望分层抽样,可参考文章:
df = df.copy().sample(600)
# C 表示告诉 Python 这是分类变量,否则 Python 会当成连续变量使用
## 这里直接使用方差分析对所有分类变量进行检验
## 下面几行代码便是使用统计学库进行方差分析的标准姿势
lm = ols('price ~ C(neighborhood) + C(style)', data=df).fit()
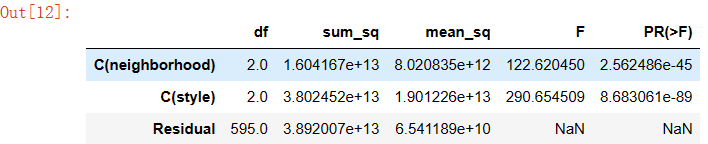
anova_lm(lm)
# Residual 行表示模型不能解释的组内的,其他的是能解释的组间的
# df: 自由度(n-1)- 分类变量中的类别个数减1
# sum_sq: 总平方和(SSM),residual行的 sum_eq: SSE
# mean_sq: msm, residual行的 mean_sq: mse
# F:F 统计量,查看卡方分布表即可
# PR(>F): P 值
2. 建立线性回归模型
- 使用
最小二乘法建立线性回归模型
from statsmodels.formula.api import ols
#最小二乘法建立线性回归模型
lm = ols('price ~ area + bedrooms + bathrooms', data=df).fit()
lm.summary()
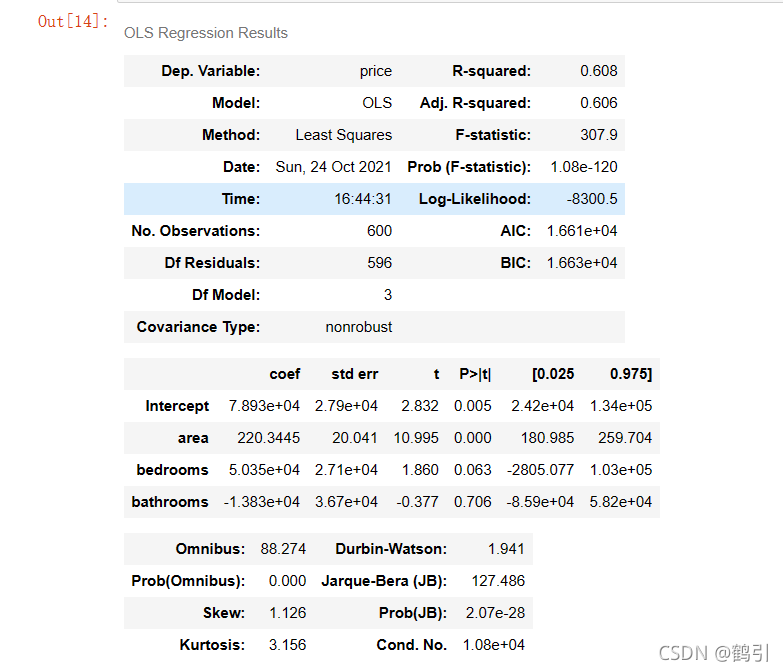
模型拟合效果不理想,
?
R
2
=
0.608
\ R^2 =0.608
?R2=0.608,模型需要进一步优化。
- 模型优化
模型精度较低,这里通过添加虚拟变量与使用方差膨胀因子检测多元共线性的方式来提升模型精度
# 设置虚拟变量
# 以名义变量 neighborhood 街区为例
nominal_data = df['neighborhood']
# 设置虚拟变量
dummies = pd.get_dummies(nominal_data)
dummies.sample() # pandas 会自动帮你命名
# 每个名义变量生成的虚拟变量中,需要各丢弃一个,这里以丢弃C为例
dummies.drop(columns=['C'], inplace=True)
dummies.sample()

结果与原数据集连接
# 将结果与原数据集拼接
results = pd.concat(objs=[df, dummies], axis='columns') # 按照列来合并
results.sample(3)
# 对名义变量 style 的处理可自行尝试
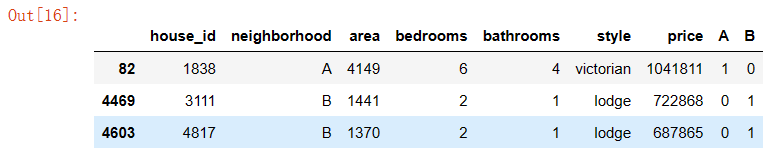
lm = ols('price ~ area + bedrooms + bathrooms + A + B', data=results).fit()
lm.summary()
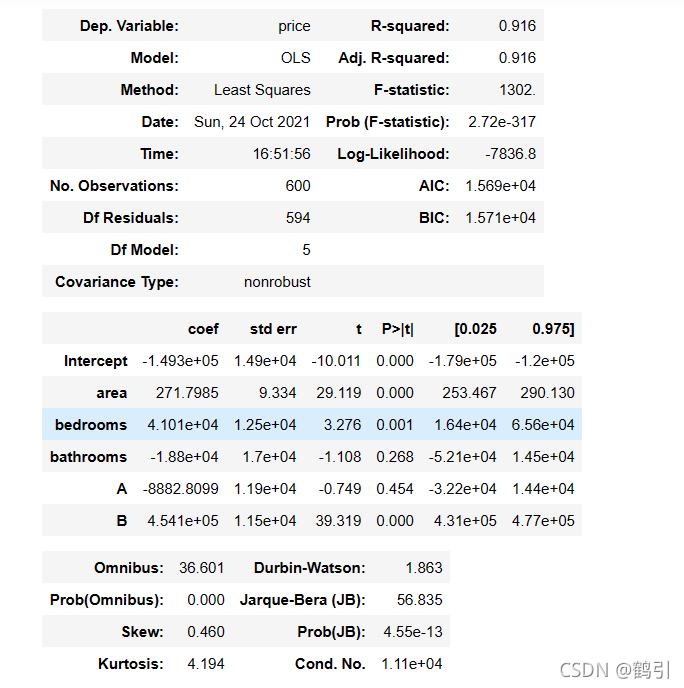
?
R
2
=
0.916
\ R^2 =0.916
?R2=0.916
3. Sklearn库建立多元线性回归模型
#导入相关库
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split #这里是引用了交叉验证
from sklearn.linear_model import LinearRegression #线性回归
from sklearn.linear_model import Lasso, Ridge, LinearRegression as LR
from sklearn.metrics import r2_score, explained_variance_score as EVS, mean_squared_error as MSE
from sklearn.model_selection import train_test_split, cross_val_score
from pandas.core.accessor import register_dataframe_accessor
- 读入数据
data=pd.read_csv('E:\人工智能\house_prices.csv')
x = data[['neighborhood','area','bedrooms','bathrooms','style']]#自变量
y= data['price']# 因变量
- 划分训练集等
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.3, random_state=1)
- 模型训练与求解

- 判断参数
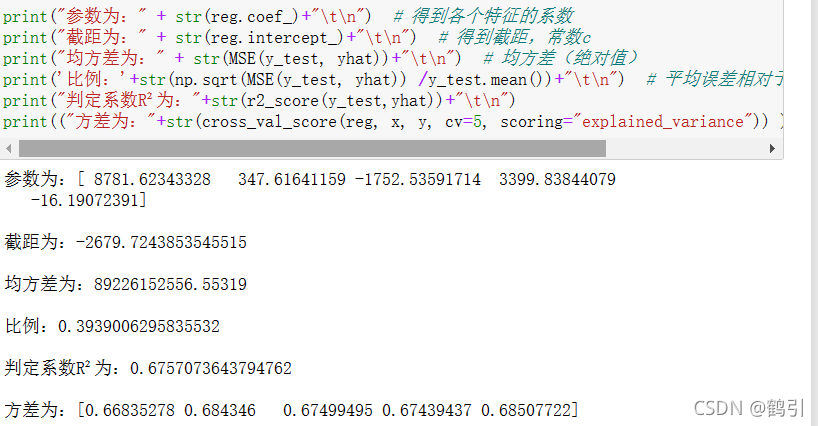
六、总结
- 使用数学方法对影响因变量的各种因素进行分析,可以快速确定自变量与因变量之间是否存在线性关系,能够帮助我们建立合适的数学模型。
Pandas库提供的数据清洗处理,Python能够更灵活的对模型进行优化,提升精度。- 使用
Excel和linear_model进行回归时,必须将非数值型数据转换为数值型数据。
七、参考
基于多元线性回归的房价预测
【机器学习】机器学习之多元线性回归
sklearn线性回归实现房价预测模型
机器学习理论(三)多元线性回归