[人工智能]【手撕LSTM】LSTM的numpy实现

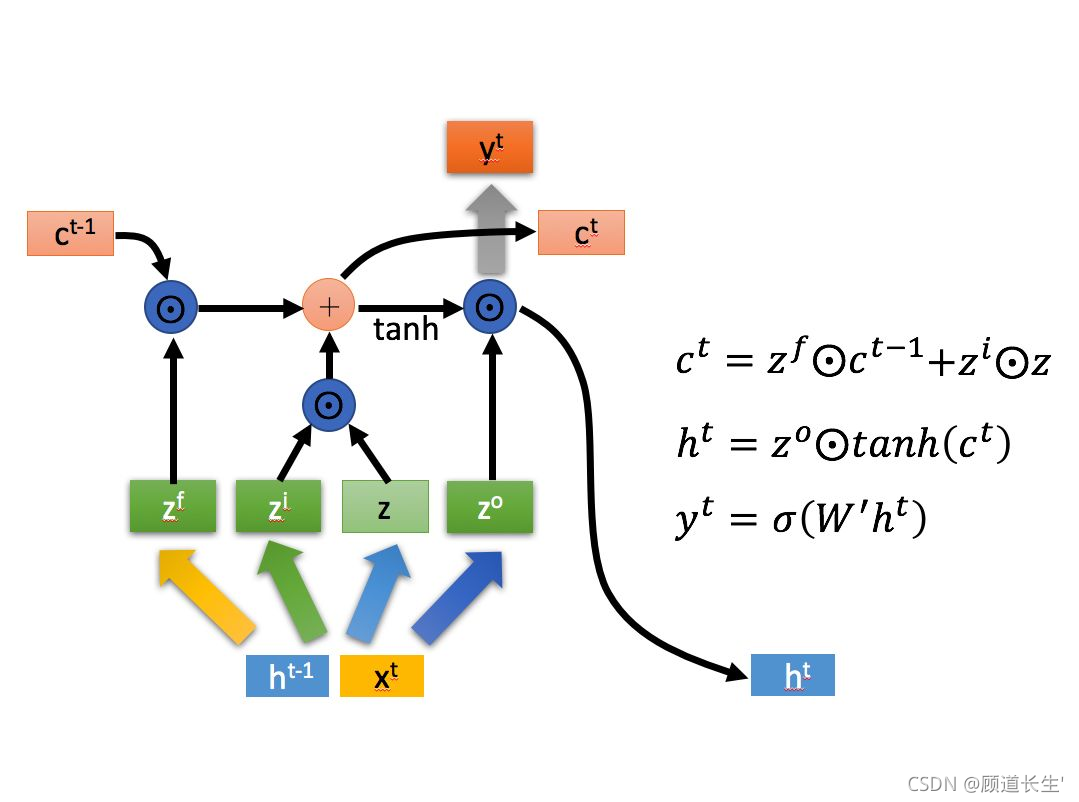
详细理论部分参考我博文（2020李宏毅）机器学习-Recurrent Neural Network

LSTM原理图

公式
$${\mathbf{F}}_t=\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xf}+{\mathbf{H}}_{t?1}{\mathbf{W}}_{hf}+{\mathbf{b}}_f\right)$$
$${\mathbf{I}}_t=\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xi}+{\mathbf{H}}_{t?1}{\mathbf{W}}_{hi}+{\mathbf{b}}_i\right)$$
$${\tilde{\mathbf{C}}}_t=\tanh \left({\mathbf{X}}_t{\mathbf{W}}_{xc}+{\mathbf{H}}_{t?1}{\mathbf{W}}_{hc}+{\mathbf{b}}_c\right)$$
$${\mathbf{C}}_t={\mathbf{F}}_t\odot {\mathbf{C}}_{t?1}+{\mathbf{I}}_t\odot {\tilde{\mathbf{C}}}_t$$
$${\mathbf{O}}_t=\sigma \left({\mathbf{X}}_t{\mathbf{W}}_{xo}+{\mathbf{H}}_{t?1}{\mathbf{W}}_{ho}+{\mathbf{b}}_o\right)$$
$${\mathbf{H}}_t={\mathbf{O}}_t\odot \tanh \left({\mathbf{C}}_t\right)$$

便于程序实现的公式（简化版公式）

$${\mathbf{F}}_t=\sigma \left({\mathbf{W}}_f[{\mathbf{H}}_{t?1},{\mathbf{X}}_t]+{\mathbf{b}}_f\right)$$
$${\mathbf{I}}_t=\sigma \left({\mathbf{W}}_i[{\mathbf{H}}_{t?1},{\mathbf{X}}_t]+{\mathbf{b}}_i\right)$$
$${\tilde{\mathbf{C}}}_t=\tanh \left({\mathbf{W}}_c[{\mathbf{H}}_{t?1},{\mathbf{X}}_t]+{\mathbf{b}}_c\right)$$
$${\mathbf{C}}_t={\mathbf{F}}_t\odot {\mathbf{C}}_{t?1}+{\mathbf{I}}_t\odot {\tilde{\mathbf{C}}}_t$$
$${\mathbf{O}}_t=\sigma \left({\mathbf{W}}_o[{\mathbf{H}}_{t?1},{\mathbf{X}}_t]+{\mathbf{b}}_o\right)$$
$${\mathbf{H}}_t={\mathbf{O}}_t\odot \tanh \left({\mathbf{C}}_t\right)$$

关于“门”

遗忘门

在LSTM中，遗忘门可以实现操作：
$${\mathbf{F}}_t=\sigma \left({\mathbf{W}}_f[{\mathbf{H}}_{t?1},{\mathbf{X}}_t]+{\mathbf{b}}_f\right)$$
在这里，$W_f$是控制遗忘门行为的权重。将$[{\mathbf{H}}_{t?1},{\mathbf{X}}_t]$连接起来，然后乘以$W_f$。上面的等式使得向量${\mathbf{F}}_t$的值介于0到1之间。该遗忘门向量将逐元素乘以先前的单元状态${\mathbf{C}}_{t?1}$。因此，如果${\mathbf{F}}_t$的其中一个值为0（或接近于0），则表示LSTM应该移除${\mathbf{C}}_{t?1}$中的一部分信息，如果其中一个值为1，则它将保留信息。

输入门

输入门的公式：
$${\mathbf{I}}_t=\sigma \left({\mathbf{W}}_i[{\mathbf{H}}_{t?1},{\mathbf{X}}_t]+{\mathbf{b}}_i\right)$$
类似于遗忘门，在这里${\mathbf{I}}_t$也是值为0到1之间的向量。这将与${\tilde{\mathbf{C}}}_t$逐元素相乘以计算${\mathbf{C}}_t$。

更新memory

新的输入向量：
$${\tilde{\mathbf{C}}}_t=\tanh \left({\mathbf{W}}_c[{\mathbf{H}}_{t?1},{\mathbf{X}}_t]+{\mathbf{b}}_c\right)$$
最后，新的memory状态为：
$${\mathbf{C}}_t={\mathbf{F}}_t\odot {\mathbf{C}}_{t?1}+{\mathbf{I}}_t\odot {\tilde{\mathbf{C}}}_t$$

输出门

为了确定接下来将使用哪些输出，使用以下两个公式：

$${\mathbf{O}}_t=\sigma \left({\mathbf{W}}_o[{\mathbf{H}}_{t?1},{\mathbf{X}}_t]+{\mathbf{b}}_o\right)$$
$${\mathbf{H}}_t={\mathbf{O}}_t\odot \tanh \left({\mathbf{C}}_t\right)$$

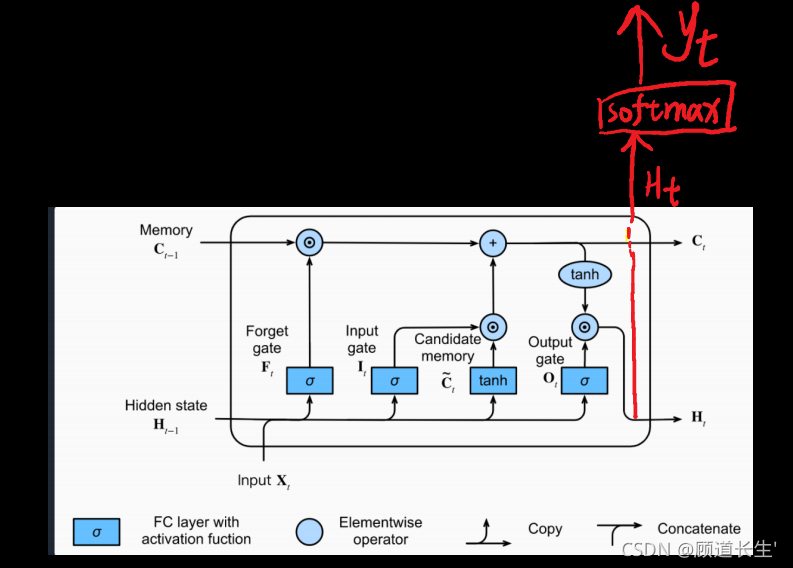
LSTM单元

实现上图中描述的LSTM单元。

说明：

1. 将${\mathbf{H}}_{t?1}$和${\mathbf{X}}_t$连接在一个矩阵中：$concat=\left[\begin{array}{c}{\mathbf{H}}_{t?1}\\ {\mathbf{X}}_t\end{array}\right]$
2. 计算以上公式，使用sigmoid()和np.tanh()。
3. 计算预测$y^{?t?}$，使用softmax()。
4. 预测$\hat{y}$公式为$\hat{y}=softmax(W_y{H}_t+b_y)$

import numpy as np

def sigmoid(x):
    return 1/(1+np.exp(-x))

def softmax(x):
    e_x = np.exp(x-np.max(x))# 防溢出
    return e_x/e_x.sum(axis=0)

def LSTM_CELL_Forward(xt,h_prev,C_prev,parameters):
    """
    Arguments:
    xt:时间步“t”处输入的数据 shape(n_x,m)
    h_prev:时间步“t-1”的隐藏状态 shape(n_h,m)
    C_prev:时间步“t-1”的memory状态 shape(n_h,m)
    parameters
        Wf 遗忘门的权重矩阵 shape(n_h,n_h+n_x)
        bf 遗忘门的偏置 shape(n_h,1)
        Wi 输入门的权重矩阵 shape(n_h,n_h+n_x)
        bi 输入门的偏置 shape(n_h,1)
        Wc 第一个“tanh”的权重矩阵 shape（n_h，n_h+n_x）
        bc 第一个“tanh”的偏差 shape（n_h，1）
        Wo 输出门的权重矩阵 shape（n_h，n_h+n_x）
        bo 输出门的偏置 shape（n_h，1）
        Wy 将隐藏状态与输出关联的权重矩阵 shape（n_y，n_h）
        by 隐藏状态与输出相关的偏置 shape（n_y，1）
    Returns:
    h_next -- 下一个隐藏状态 shape（n_h，m）
    c_next -- 下一个memory状态 shape（n_h，m）
    yt_pred -- 时间步长“t”的预测 shape（n_y，m）
    """
    # 获取参数字典中各个参数
    Wf = parameters["Wf"]
    bf = parameters["bf"]
    Wi = parameters["Wi"]
    bi = parameters["bi"]
    Wc = parameters["Wc"]
    bc = parameters["bc"]
    Wo = parameters["Wo"]
    bo = parameters["bo"]
    Wy = parameters["Wy"]
    by = parameters["by"]
    
    # 获取 xt 和 Wy 的维度参数
    n_x, m = xt.shape
    n_y, n_h = Wy.shape
    
    #拼接 h_prev 和 xt
    concat = np.zeros((n_x+n_h,m))
    concat[: n_h, :] = h_prev
    concat[n_h :, :] = xt
    
    # 计算遗忘门、输入门、记忆细胞候选值、下一时间步的记忆细胞、输出门和下一时间步的隐状态值
    ft = sigmoid(np.dot(Wf,concat)+bf)
    it = sigmoid(np.dot(Wi,concat)+bi)
    cct = np.tanh(np.dot(Wc,concat)+bc)
    c_next = ft*c_prev + it*cct
    ot = sigmoid(np.dot(Wo,concat)+bo)
    h_next = ot*np.tanh(c_next)
    
    # LSTM单元的计算预测
    yt_pred = softmax(np.dot(Wy, h_next) + by)
    
    return h_next,c_next,yt_pred

np.random.seed(1)
xt = np.random.randn(3,10)
h_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

h_next, c_next, yt = LSTM_CELL_Forward(xt, h_prev, c_prev, parameters)
print("a_next[4] = ", h_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)

a_next[4] =  [-0.66408471  0.0036921   0.02088357  0.22834167 -0.85575339  0.00138482
  0.76566531  0.34631421 -0.00215674  0.43827275]
a_next.shape =  (5, 10)
c_next[2] =  [ 0.63267805  1.00570849  0.35504474  0.20690913 -1.64566718  0.11832942
  0.76449811 -0.0981561  -0.74348425 -0.26810932]
c_next.shape =  (5, 10)
yt[1] = [0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
 0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape =  (2, 10)

预期输出:
a_next[4] = [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482
0.76566531 0.34631421 -0.00215674 0.43827275]

a_next.shape = (5, 10)

c_next[2] = [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942
0.76449811 -0.0981561 -0.74348425 -0.26810932]

c_next.shape = (5, 10)

yt[1] = [0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
0.00943007 0.12666353 0.39380172 0.07828381]

yt.shape = (2, 10)

参考
https://zh-v2.d2l.ai/chapter_recurrent-modern/lstm.html
https://www.heywhale.com/mw/project/6174b96ef7e7c300175739cc