视频可以在b站上搜到。官方实录:https://www.pazhoulab.com/2021/08/1843/
机器学习的先验假设
机器学习问题能非常好地科学化为一个数学上的最优化问题:
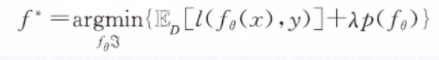
第一个是有关损失函数的独立性假设;第二个是假设空间大容量假设;第三个是训练数据的完备性假设;第四个是关于正则项设置的正则项假设;第五个是有关分析方法的欧式假设。这五个假设反映了我们大家通常用机器学习/深度学习时的选择习惯。
1、独立性假设
我们总是默认假设损失函数的选择是与问题无关的。
思路:
假定标签y与特征x之间满足一个确定性的近似关系,外加一个随机误差ε(即满足可加的生成模型),根据概率论,则立即知道,这个标签预测正确的概率是唯一由误差ε 决定的的,而且此时可由极大似然估计来估计参数。
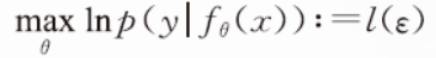
基于这个观察,可以很快推出并实验证实:当问题的误差是白噪声时,最好的损失度量的确是最小二乘,而如果误差是拉普拉斯噪声,最好的损失度量却是最小一乘;类似地,如果误差服从指数分布,最好的损失度量则是p 范数。只要知道生成数据的误差分布,就能求出最优的损失函数形式。徐院士将这个作法总结出来,叫做误差建模原理。换言之,最优的损失度量可按误差建模原理确定。作为一般应用,徐院士证明了“当数据误差是混合高斯分布时,最优的损失度量是加权最小二乘度量”。由于任意未知误差可通过高斯混合任意逼近,这一结论有应用的普适性。
2、大容量假设 4、正则项假设
我们总是假定自己用到的网络结构已经包含了最优解或近似解。我们认为根据经验设定正则项是可行的。
思路:
可以用相近的思路来解决这两个假设。假设空间怎样才能在开始时就设计到最小,这是不太可能解决的问题。我们解决问题的思路是,用粗糙的模型( 称为模型簇,含大量超参数的模型) 来界定解所满足的空间,用模型族导出寻找解的算法族,然后将算法映射到深度神经网络结构,最后用深度学习调参找到问题解。
我们这个方法叫做“模型驱动的深度学习”,它保证了使用越来越小、渐近最优的假设空间去执行机器学习。不仅如此,这个方法既解决了深度学习的设计方法问题,也缓解了深度学习的可解释性问题。
在不容易精确的地方加进很多待定的超参数(叫做模型簇)
- 这样粗糙的建模可以大大地减轻数学和物理学本身的困难,同时增加了人工智能应用的空间。
- 基于粗糙的模型就可以进行理论研究、数学性质研究和求解方法研究,从而形成找解的方法簇,即含有大量超参数的算法。
一旦这个方法簇形成,就能转成深度学习所使用的深度学习的深度结构。因为深度网络本身可看成是实现有限步的迭代法,这和所导出的方法簇(假定是迭代法簇)完全一致。这是最优化迭代算法与深度学习能打通的核心和关键。最后用深度学习学习出超参。
3、完备性假设
不得不总是假定这个数据集是完全代表的、高质量的、少噪声的、分布均衡的;换句话说,是个完备的大数据集。如果没有足够的量,没有高质量标签,很难得到很好的结果。
思路:
现实中数据标签可能是不够的、不准确的、不平衡的。能不能对错标得不太离谱的数据用机器学习方法,让它能够很稳健的工作?
在一定条件下,这是可能的,即是课程- 自步学习理论。
课程学习的想法最早由Bengio教授2009年提出,他提出将人类学习过程按从简单到复杂的难易程度设置课程按照不同年级、不同课程实施教育的过程变成算法,来处理标签不好的数据。后来Koller教授2010年提出了实现Bengio想法的自步算法。Koller的算法是一个硬阈值的算法,即引进一个随时间改变的难度阈值,当损失函数小于这个阈值的数据安排来当前学习,否则不学习。这种方法很难设置阈值,结果不理想。徐院士及其团队在这个问题上做出的贡献:
- 将课程-自步学习纳入正则化框架,提出了正则化函数满足什么样的条件能达到课程- 自步学习的公理化条件。
- 理论上证明了课程-自步学习的本质是使用非凸损失函数的稳健机器学习。通过引进隐式攒失函数,建立了课程-自步学习的凹共轭理论,说明任何课程-自步学习策略等价于使用一个非凸出数作损失的常规机器学日算法。
- 提出了自动设计自步正则项和年龄参数的元学习算法,全面实现了课程-自步学习 算法的自动化。
5、欧式假设
假设机器学习参数能够自然嵌入到我们熟悉的欧几里得空间中。这个假设则限制了我们对很多不能放在欧式空间分析或者使用的算法之分析。
思路:
要分析收敛性、泛化性和计算复杂性等,就必须把相应算法放在一个合适的平台上,这个平台就是数学上的空间。
为什么我们会不自觉地去用2范数去作这样的估计?因为用2范数能够把要估计的量再分拆,即不加任何放大、不加任何粗糙化地把它展成3项,其中每一项都有更加确定的意义和更方便分析。
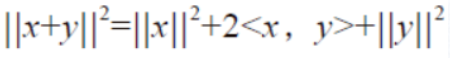
这个欧氏假设非常方便我们去分析数据拟合项和正则项都为2范数的情形,但不允许我们去分析p≠2 的拟合项和正则项。
1991年徐院士和英国数学家G.F. 罗奇联合发表了现在被广泛称之为“徐- 罗奇”定理的“巴拿赫空间特征不等式数量律”。巴拿赫空间几何可以帮我们在突破欧式假设上开辟一条新路。