一、实验原理
1.什么是逻辑回归 (LogisticRegression)
? ? ? ? 逻辑回归实际上是一种分类模型,往往用来解决二分类问题(0 or 1)。比如某用户购买某商品的可能性,某病人患有某种疾病的可能性。

Logistic 回归的本质是:假设数据服从某种分布,然后使用极大似然估计做参数的估计。
sigmoid 函数:
????????逻辑回归名字的由来是因为算法流程中使用到了一个关键的 Logisitic 函数,该函数是一个比较简单的单调递增函数,逻辑回归用 sigmoid 函数来计算样本对应的后验概率。
表达式和图像如下:
?
其中,X是我们的训练样本输入,w就是我们需要求的参数,Y是最后的结果分类标签(0,1)
2.如何得到模型的函数
逻辑回归模型的数学形式确定后,剩下就是如何去求解模型中的参数。
在统计学中,常常使用极大似然估计法来求解,即找到一组参数,使得在这组参数下,我们的数据的似然度(概率)最大。
似然函数:
为了更方便求解,我们对等式两边同取对数,写成对数似然函数:
?
?找到令l(w)最大的w,就是我们要找的模型
?在l(w)公式上加个负号,得到的损失函数表示![]()
?我们发现交叉熵公式跟之前的逻辑回归损失函数完全一致,也就是说逻辑回归的损失函数其实就是交叉熵
?3.如何求解最小化代价函数
求得代价函数后,接下来的任务就是最小化代价函数,常见的方法就是梯度下降法,
梯度公式推导如下:
对似然函数求导得到梯度![]()
?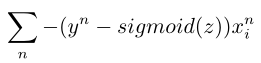
?所以梯度下降时候的迭代式子为:

为了防止过拟合加入正则项后为:
 ??
??
?二、实验过程
1.生成数据:
首先我们要生成测试数据,分别是高斯分布的正例数据和反例数据
此方法需要用到的函数:
①生成一个多元正态(高斯)分布矩阵:
def multivariate_normal(mean, cov, size=None, check_valid=None, tol=None):
"""
mean:均值μ,n维分布的平均值,是一个一维数组长度为N.
cov:协方差矩阵,它的形状必须是(n,n),注意:协方差矩阵必须是对称的且需为半正定矩阵;
size:指定生成的正态分布矩阵的维度
(例:若size=(1, 1, 2),则输出的矩阵的shape即形状为 1*1*2*N(N为mean的长度))。
check_valid:这个参数用于决定当cov即协方差矩阵不是半正定矩阵时程序的处理方式,它一共有三个值: warn,raise以及ignore。当使用warn作为传入的参数时,如果cov不是半正定的程序会输出警告但仍旧会得到结 果;当使用raise作为传入的参数时,如果cov不是半正定的程序会报错且不会计算出结果;当使用ignore时忽略 这个问题即无论cov是否为半正定的都会计算出结果。
"""②list和numpy数组的“:”操作
a[:n]?意思是取出a中的前n个元素
a[n:]?表示输出a的从第n个元素到最后一个元素
list[::]?的意思是?list[start:end:step][m::n]? 后面的n是取元素的间隔,从下标为m的元素开始取,接着是下标为m+n的元素,直到结束
?正例数据在前,反例数据在后
def getData(n, mean_0, mean_1, variance, cov_xy):
"""
生成是高斯分布的两类数据
:param n: 每一类样本的个数
:param mean_0: 反例样本均值
:param mean_1: 正例样本均值
:param variance: 样本方差
:param cov_xy: 样本协方差
:return: 训练集x与y
"""
# 初始化
train_x = np.ones((n * 2, 3))
train_y = np.zeros(n * 2)
# 获得两类数据,正例在前,反例在后
train_x[:n, 1:] = np.random.multivariate_normal(mean_0, [[variance, cov_xy], [cov_xy, variance]], n)
train_x[n:, 1:] = np.random.multivariate_normal(mean_1, [[variance, cov_xy], [cov_xy, variance]], n)
train_y[:n] = 0
train_y[n:] = 1
return train_x, train_y?
2.梯度下降法
使用实验1中接触到的梯度下降法最小化代价函数
输入训练集x,训练集真实类别y,
param eta: 学习率
param penality_lambda: 正则项系数
当前梯度与步长迭代后会使得损失函数下降后 更新θ
直到梯度变成一个极小值或者迭代到一定次数后退出迭代
3.计算正确率
计算ω ? x 的值,与0比较,若大于或者等于零预测为1;小于0预测为0.统计预测正确的样本数correct_count ,计算预测的正确率correct_count / train_size
4.读取实际数据
采用了 UCI 网站上找到 Skin_NonSkin.txt 文件进行测试,由于每一个数据都是三维的,所以画了三维的图来显式地表示分类情况。
?绘制3D图像
? #绘制样本点
? ? ax.scatter(train_x[:, 0], train_x[:, 1], train_x[:, 2], c=train_y, cmap=plt.cm.RdYlGn)
? ? #绘制平面
? ? real_x = np.arange(-200, 250, 50)
? ? real_y = np.arange(-200, 250, 50)
? ? real_X, real_Y = np.meshgrid(real_x, real_y)
? ? real_z = coefficient[0] + coefficient[1] * real_X + coefficient[2] * real_Y
? ? ax.plot_surface(X=real_X, Y=real_Y, Z=real_z, rstride=1, cstride=1)
读取数据时,由于样本数量过于庞大,采取500的步长选取数据,并对样本点x值进行100的坐标平移便于显示
? ? load_data = np.loadtxt('./Skin_NonSkin.txt', dtype=np.int32)
? ? train_data = load_data[:load_data_size, :] ?# 训练集数据
? ? train_x = train_x[::step]
? ? train_x = train_x - 100 ?# 对样本点进行坐标平移
三、实验结果与分析
1.有惩罚项,满足朴素贝叶斯假设
?===============================>有无正则项
#生成两组组均值分别是[?2,?2],[2,2],方差为2,协方差为0,正则项权重为0 的高斯分布样本点,用梯度下降法进行迭代求解的结果:
无正则项:

有正则项=0.001 (表现最好的正则值)

2.不满足/满足朴素贝叶斯假设
===========================>是否符合朴素贝叶斯
Gaussian_test(100, [-2, -2], [2, 2], 3, 0.5, 0.001, 1000000, 10) ? ?#93%(cov=0.5)

?
?Gaussian_test(100, [-2, -2], [2, 2], 3, 2, 0.001, 1000000, 10) ? ? ?#89.5%(cov=2)
?

?
?Gaussian_test(100, [-2, -2], [2, 2], 3, 5, 0.001, 1000000, 10) ? ? ?#83%(cov=5)

通过以上的测试可以看出,
在二维条件下,是否有惩罚项对分类影响不大,但当减小训练集时,所得到的判别函数确实存在过拟合现象,加入正则项可以预防此现象的发生。?
逻辑回归分类器在在满足朴素贝叶斯假设时分类良好,在不满足朴素贝叶斯假设时且协方差较小时,分类效果也与满足时相差并不大,可能是由于数据维度只有二维,不会发生较大的偏差。不过cov过大时正确率会存在下降。
3.真实skin数据集测试
1)Skin_NonSkin.txt
accuracy rate: 94.09%

?2)Iris3Txt
由于是多维数据没有做图,accuracy rate: 96.67%

?在UCI数据的表现大致相同,判别准确率在90%~95%,在一些数据很差的数据集中准确率有所下降(比如正例反例数量不均等)
?
?四、结论
1.逻辑回归并没有对数据的分布进行建模,也就是说,逻辑回归模型并不知道数据的具体分布,而是直接根据已有的数据求解分类超平面。
2.逻辑回归可以很好地解决线性分类问题,而且收敛速度较快,在真实的数据集上往往只需要数百次的迭代就能得到结果。
3.正则项在数据量较大时,对结果的影响不大。在数据量较小时,可以有效解决过拟合问题。
4.从结果中可以看出,模型在满足朴素贝叶斯假设时的分类表现略好于不满足朴素贝叶斯假设时。
5.在 UCI 上找的数据以及自己的生成数据上的准确率基本都在 90% 以上,说明逻辑回归是一个比较不错的线性分类模型。但数据本身的分布对实验结果影响较大,需要满足数据本身就是线性可分的,否则正确率下降严重
?

