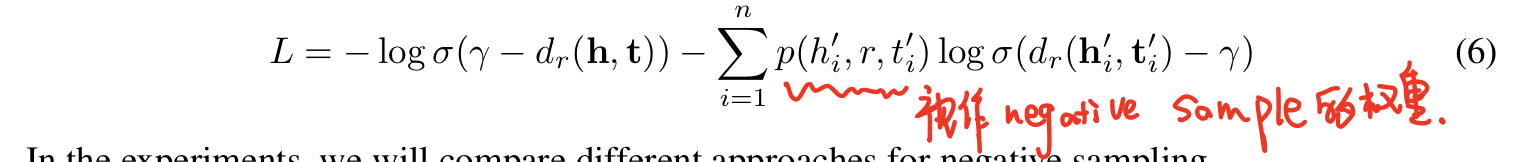abstract

研究在知识图中学习实体和关系的表征来预测缺失links的任务。这种任务的成功很大程度上取决于建模和推断关系的模式上。本文提出了一种全新的知识嵌入图的方法RotatE，可以建模和推断各种关系模式：对称/非对称，反转，组成。RotatE将每种关系建模为在复向量空间中从源实体到目标实体的一个旋转（rotate）。除此以外，我们还提出了一种全新的self-adversarial 负采样技术来进行RotatE模型的有效性训练。实验证明，RotatE不仅是具有可扩展性的，也可以推断和建模各种各样的关系模式，在链接预测模式上可以超越现存的SOTA方法。

1.introduction

从observed facts中找到方法来建模和推断模式（如：对称性/不对称性，反转，组成）在预测missing links中是很重要的。但是，现存的方法没有办法建模以上这些所有的模式，于是我们找到方法来建模和推断以上三种类型的关系模式。

我们的motivation来自于Euler identity： $e^{i\theta} =cos \theta+ i \,sin \theta$ ，它表明一个复数可以被视为是复平面（complex space）的一个旋转。给定一个三元组 $(h, r, t)$ ，我们期望 $\circ r$ ，其中 $\in \mathbb{C}^k$ 是embeddings，以及 $r_i|=1$ , $\circ$ 代表哈达玛积。对于复平面中的每一个维度，我们期望：

t_i =h_i r_i ，h_i,r_i,t_i \in \mathbb{C},|r_i|=1.

这样一个简单的操作，可以有效建模之前提到的三种关系：symmetric/antisymmetric，inversion，composition。举例说明：一个relation $r$ 是对称的iff embedding $r$ 的每个成分满足 $r_i = e^{0/i\pi}=\pm 1.$ 两个关系是inverse iff 它们的embedding是conjugates（共轭的）: $r_2 = \bar{r_1}$ ，一个关系 $r_3 =e^{i \theta_3}$ 是两个关系 $r_2 =e^{i \theta_2},r_1 =e^{i \theta_1}$ 的组合 iff $r_3 = r_1 \circ r_2 (\theta_3 =\theta_1 +\theta_2)$ 。进一步的，RotatE可以扩展到大的知识图上去，因为它在时间和空间上几乎是线性的。

为了有效优化RotatE，我们进一步提出了一个self-adversarial 负采样方法，根据目前的实体和关系来生成负样本。这种方法非常通用可以被用于许多现有的知识图嵌入方法中。实验证明，RotatE达到了SOTA。

2.related work

3.RotatE：relational rotation in complex vector space

3.1 modeling and inferring relation patterns

在知识图中三种非常重要的关系模式：summery，inversion and composition。给出它们的定义:\
定义1:一个关系 $r$ 是对称的/反对称的，若对 $\forall x,y:$

\Rightarrow r(y,x)(r(x,y) \Rightarrow \neg r(y,x))

定义2:一个关系 $r_1$ 是关系 $r_2$ 的inverse，若对 $\forall x,y:$

r_2(x,y)\Rightarrow r_1(x,y)

定义3:一个关系 $r_1$ 由 $r_2,r_3$ 构成，若对 $\forall x,y,z:$

r_2(x,y)\bigcap r_3(y,z)\Rightarrow r_1(x,z)

请添加图片描述

3.2 modeling relations as rotations in complex vector space

给定一个三元组 $(h, r, t)$ ：

\circ r，where \, |r_i| =1

对于embedding中的每一个元素，我们都有 $t_i = h_i r_i$ ，且 $h,t\in \mathbb{C}^k$ ， $r_ i \in \mathbb{C}, |r_i|=1$ ,因此 $r_i$ 具有形式 $e^{i \theta_{r,i}}$ ，是关于复平面中的原点的 $\theta_{r,i}$ 的逆时针旋转，仅仅影响负向量空间中的实体嵌入。我们称提出的模型为RotatE由于它的旋转特性。根据以上的定义，对于每个三元组 $(h, r, t)$ ，我们定义RotatE的距离函数如下:

d_r(h,t) =||h \circ r - t||

通过定义每个关系为复向量空间中的旋转，RotatE是唯一可以建模以及推断上面三种关系模式的模型。

3.3 optimization

我们使用了和负采样损失相似的损失函数来有效优化基于距离的模型：

\, \sigma(\gamma-d_r(h,t))-\sum\limits_{i=1}^n \frac{1}{k}log \, \sigma (d_r(h_i',t_i')-\gamma),

其中 $\gamma$ 是固定的margin， $h_i',r,t_i')$ 是i-th negative triplet。

我们也提出了一种新的方法来生成负样本。负采样损失使用一种uniform的方法来采样negative triplets。这样的均匀的负采样方法具有效率不高的问题（因为很多的样本随着训练的进行很明显是错误的，并不能提供任何有意义的信息）。因此我们提出了一个称为self-adversarial的负采样，它根据目前的embedding模型采样出negative triples。具体来说，我们从下面的分布中采样出negative triples：
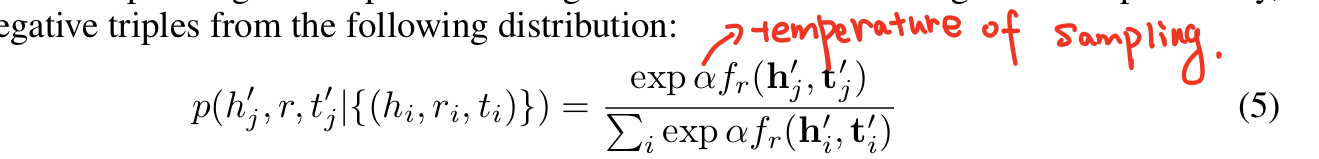
请添加图片描述
最终的带有self-adversarial training 的负采样损失的形式：