核心思想
??本文提出了一种基于学习的带有几何约束的局部特征描述算法,作者提出一种几何相似性的度量方法,并根据几何相似性改进了训练集的采样方法及损失函数。作者认为如果两个匹配图块之间的几何相似性太高,也就是两幅图像拍摄的角度比较接近时,这样的匹配图块对于网络的训练作用有限,因为太容易了。因此作者希望在采样过程中选择出那些几何相似性更低的,匹配难度更大的图块,这能够为网络的训练提供更多有用的信息。
??和LIFT算法一样,首先利用3D重建数据集获取正确的2D匹配点,根据不同角度拍摄的同一个目标的图像,使用SfM算法获得稀疏的3D重构点云,重构出来的部分就表示两幅图像之间正确匹配。然后将3D点云中的点重新映射到各个图像上,得到2D匹配点。在此基础上,作者又引入的3D Delaunay三角剖分方法用于能见度检测,进一步筛除误匹配点,提高数据的质量。
??对每个2D匹配点都生成一个对应的匹配图块,生成方式如下
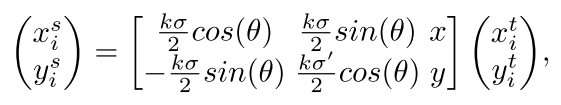
(
x
i
s
,
y
i
s
)
(x^s_i,y^s_i)
(xis?,yis?),
(
x
i
t
,
y
i
t
)
(x^t_i,y^t_i)
(xit?,yit?)分别表示输入和输出的规则采样网格坐标(原文中这样写的,我感觉输入输出是不是反了?),
(
x
,
y
,
σ
,
θ
)
(x,y,\sigma,\theta)
(x,y,σ,θ)为匹配点的参数,分别表示
x
,
y
x,y
x,y坐标,尺度和方向,这些参数可以通过SIFT描述器获得。
??接下来是计算匹配图块之间的几何相似性,作者提出两个计算方式一个是图块之间的相似性(Patch similarity),另一个是图像之间的相似性(Image similarity)。图块之间的几何相似性描述了从不同视角下获取的一对图块之间的匹配难度,相似性越高,匹配难度越低。首先给定一对匹配图块,将其与以
C
i
C_i
Ci?和
C
j
C_j
Cj?为中心的摄像机所看到的相应的3D轨迹
P
P
P联系起来。我理解
P
P
P点就是两个匹配图块对应的3D关键点,因为两个匹配图块是由两个2D匹配点得到的,而两个2D匹配点必然对应空间中的一个3D关键点,
C
i
C_i
Ci?和
C
j
C_j
Cj?就是拍摄两个图块的相机的中心位置。然后计算
P
P
P点处的法线向量
P
n
P_n
Pn?,如下图所示
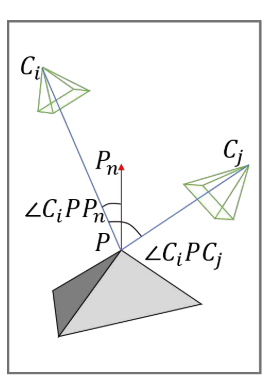
图块相似性的计算方法如下
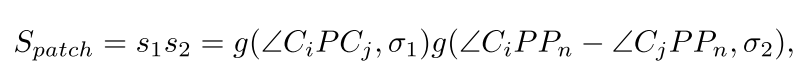
s
1
s_1
s1?计算了两个观察光线之间的夹角,
s
2
s_2
s2?计算了两个入射角之间的差异,
g
(
α
,
σ
)
g(\alpha,\sigma)
g(α,σ)是一种角度计算方法,过程如下
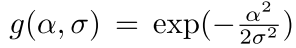
图像之间的相似性就是两幅匹配图像之间所有匹配图块相似性的平均值。

??下面构建每个batch训练匹配图块集,L2-Net和HardNet是从整个数据集中随机采样得到每个Batch的训练集,而本文提出的方法是从一对匹配图像之间构建每个Batch的训练图块集。给定一对匹配图像,从中获取一组匹配图块集
X
=
{
(
x
1
,
x
1
+
)
,
(
x
2
,
x
2
+
)
,
(
x
3
,
x
3
+
)
.
.
.
(
x
N
1
,
x
N
1
+
)
,
}
X=\{(x_1,x_1^+),(x_2,x_2^+),(x_3,x_3^+)...(x_{N_1},x_{N_1}^+),\}
X={(x1?,x1+?),(x2?,x2+?),(x3?,x3+?)...(xN1??,xN1?+?),},
(
x
1
,
x
1
+
)
(x_1,x_1^+)
(x1?,x1+?)表示一对匹配图块,
N
1
N_1
N1?表示匹配图块集合的大小。每个batch的训练图块集是从
N
2
N_2
N2?个匹配图块集合中采样构建起来。作者还将图块几何相似性超过0.85的图块删除掉了。这样做的好处是每个batch中的图块都是比较相似的,给训练带来更大的难度。
实现过程
网络结构
??网络结构借用了L2-Net中的结构,并且使用带有步长的卷积层取代了池化层,除了最后一层其他卷积层后面均带有BN层,最后用一个L2正则化层将卷积层的输出规范化为128维的特征向量。
损失函数
??损失函数包含两个部分结构化损失(Structured loss)和几何损失(Geometric loss)。
??结构化损失保证了匹配图块和误匹配图块之间有一定的距离,首先给定一个匹配图块集合
X
X
X,然后计算图块集合中每对匹配图块的特征向量
F
1
,
F
2
∈
R
N
1
×
128
F_1,F_2\in \mathbb{R}^{N_1\times 128}
F1?,F2?∈RN1?×128之间的余弦相似度
S
=
F
1
F
2
T
S=F_1F_2^T
S=F1?F2T?,然后计算
L
=
S
?
α
d
i
a
g
(
S
)
L=S-\alpha diag(S)
L=S?αdiag(S),再计算结构化损失
E
1
E_1
E1?
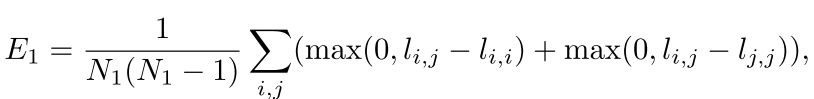
l
i
,
j
l_{i,j}
li,j?是
L
L
L中的元素。
??几何损失则是使得匹配图块在度量空间中的距离更近。作者根据图块的几何相似性来设置不同阈值,对于匹配难度越大的图块,则认定二者正确匹配的阈值越低。
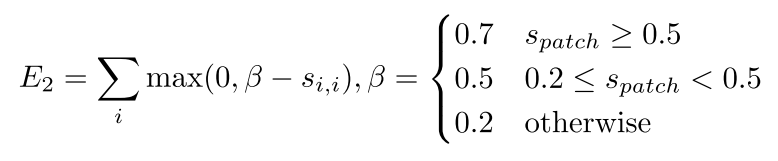
创新点
- 提出一种几何相似性度量的方法
- 基于上述度量方法,提出一种新的训练集构建方法以及损失函数
算法评价
??本文主要是从利用几何相似性来反映匹配难度的角度出发,先是确定了一种集合相似性的度量方法,然后利用几何相似性从数据集中选择出匹配难度更大的图块,来构成每个batch的训练集。然后在损失函数构建方面,也考虑了几何相似性的影响,让损失函数中的阈值能够随着匹配难度自适应的调整。
如果大家对于深度学习与计算机视觉领域感兴趣,希望获得更多的知识分享与最新的论文解读,欢迎关注我的个人公众号“深视”。