三维点云课程—Special Clustering代码
from sklearn import datasets
import numpy as np
from sklearn.cluster import KMeans
from matplotlib import pyplot as plt
from itertools import cycle, islice
# 计算两个坐标之间的欧氏距离
def distance(x1, x2):
res = np.sqrt(np.sum((x1 - x2) ** 2))
return res
# 计算数据之间的距离矩阵,分别计算一个坐标与其他坐标间的距离
def distanceMatrix(X):
M = np.array(X)
Z = np.zeros((len(M), len(M)))
for i in range(len(M)):
for j in range(i + 1, len(M)):
Z[i][j] = 1.0 * distance(X[i], X[j])
Z[j][i] = Z[i][j]
return Z
# 计算相似矩阵,采用KNN法+高斯核函数,Z距离矩阵,k聚类数
def adjacencyMatrix(Z, k, sigma=1.0):
N = len(Z)
A = np.zeros((N, N))
for i in range(N):
"""
>>>a = [1,2,3]
>>> b = [4,5,6]
>>> c = [4,5,6,7,8]
>>> zipped = zip(a,b) # 打包为元组的列表
[(1, 4), (2, 5), (3, 6)]
>>> zip(a,c) # 元素个数与最短的列表一致
[(1, 4), (2, 5), (3, 6)]
>>> zip(*zipped) # 与 zip 相反,*zipped 可理解为解压,返回二维矩阵式
[(1, 2, 3), (4, 5, 6)]
"""
dist = zip(Z[i], range(N)) # 将Z矩阵的一行内的元素进行逐个标识下标(下标从0-range(N))
dist_index = sorted(dist, key=lambda x: x[0]) # 根据X[0]=dist[i][0]的元素进行从小到大排序
neibours_id = [dist_index[m][1] for m in range(k + 1)] # 挑出排序前K的元素的下标索引
sigma=np.var(Z)/4
for index in neibours_id:
A[i][index] = np.exp(-(Z[i][index]**2) / (2 * sigma * sigma))
A[index][i] = A[i][index]
return A
# 计算拉普拉斯矩阵及其特征矩阵,A相似矩阵,k聚类数
def laplacianMatrix(A,k):
# 计算对角矩阵D
D = np.sum(A, axis=1)
# 计算普通的拉普拉斯矩阵
L = np.diag(D) - A
# 计算标准化之后的拉普拉斯矩阵
squareD = np.diag(1.0 / (D ** (0.5)))
#Lsym=I-D^(-1/2)*W*D^(-1/2)=D^(-1/2)*L*D^(-1/2)
standardization_L = np.dot(np.dot(squareD, L), squareD)
# 计算标准化拉普拉斯矩阵的特征值和特征向量
x, V = np.linalg.eig(standardization_L)
V=V.astype(float)
# y=np.copy(x)
# z=np.partition(y,list(range(len(y))))
# n_cluster=0;
# diff_value=abs(abs(z[1])-abs(z[0]))
# for i in range(1,len(z)):
# if abs(abs(z[i-1])-abs(z[i]))>diff_value*2 and abs(z[i-1])*3<abs(z[i]):
# n_cluster=i+1
# break
# diff_value=abs(abs(z[i-1])-abs(z[i]))
# print (n_cluster)
# 将特征值进行排序
idx_k_smallest = np.where(x < np.partition(x, k)[k])
H = np.hstack([V[:, i] for i in idx_k_smallest])
return H
def read_txt(path):
filename = path # txt文件和当前脚本在同一目录下,所以不用写具体路径
pos = []
Efield = []
with open(filename, 'r') as file_to_read:
while True:
lines = file_to_read.readline() # 整行读取数据
if not lines:
break
pass
p_tmp, E_tmp = [float(i) for i in lines.split(",")] # 将整行数据分割处理,如果分割符是空格,括号里就不用传入参数,如果是逗号, 则传入‘,'字符。
pos.append(p_tmp) # 添加新读取的数据
Efield.append(E_tmp)
pass
pos = np.array(pos) # 将数据从list类型转换为array类型。
Efield = np.array(Efield)
x=np.vstack(pos)
y=np.vstack(Efield)
X=np.concatenate((x,y),axis=1)
return X
fig, ax = plt.subplots(4, 2)
def show_result(x,i,j,n_labels):
ax[i][j].scatter(x[:, 0], x[:, 1], s=20, c="b", marker='o')
ax[i][j].set_xlabel('x')
ax[i][j].set_ylabel('y')
list_max = max(n_labels)
if list_max == 1:
for idx, value in enumerate(n_labels):
if value == 0:
ax[i][j+1].scatter(x[idx, 0], x[idx, 1], s=20, c="r", marker='*')
elif value == 1:
ax[i][j+1].scatter(x[idx, 0], x[idx, 1], s=20, c="g", marker='+')
elif list_max == 2:
for idx, value in enumerate(n_labels):
if value == 0:
ax[i][j+1].scatter(x[idx, 0], x[idx, 1], s=20, c="r", marker='*')
elif value == 1:
ax[i][j+1].scatter(x[idx, 0], x[idx, 1], s=20, c="g", marker='+')
elif value == 2:
ax[i][j+1].scatter(x[idx, 0], x[idx, 1], s=20, c="y", marker='^')
ax[i][j+1].set_xlabel('x')
ax[i][j+1].set_ylabel('y')
if __name__ == '__main__':
data_circle=read_txt("circle.txt")
Z_circle = distanceMatrix(data_circle)
M_cicle = adjacencyMatrix(Z_circle, 5)
H_cicle = laplacianMatrix(M_cicle,2)
sp_circle = KMeans(n_clusters=2).fit(H_cicle)
show_result(data_circle,0,0,sp_circle.labels_)
print("the first cluster successful")
data_moons = read_txt("moons.txt")
Z_moons = distanceMatrix(data_moons)
M_moons = adjacencyMatrix(Z_moons, 6)
H_moons = laplacianMatrix(M_moons,2)
sp_moons = KMeans(n_clusters=2).fit(H_moons)
show_result(data_moons, 1, 0, sp_moons.labels_)
print("the second cluster successful")
data_varied = read_txt("varied.txt")
Z_varied = distanceMatrix(data_varied)
M_varied = adjacencyMatrix(Z_varied, 30)
H_varied = laplacianMatrix(M_varied,3)
sp_varied = KMeans(init='k-means++',n_clusters=3,tol=1e-6).fit(H_varied)
show_result(data_varied, 2, 0, sp_varied.labels_)
print("the third cluster successful")
data_aniso = read_txt("aniso.txt")
Z_aniso = distanceMatrix(data_aniso)
M_aniso = adjacencyMatrix(Z_aniso, 20)
H_aniso = laplacianMatrix(M_aniso,3)
sp_aniso = KMeans(init="k-means++",n_clusters=3,tol=1e-6).fit(H_aniso)
show_result(data_aniso, 3, 0, sp_aniso.labels_)
print("the fourth cluster successful")
plt.show()
仿真结果
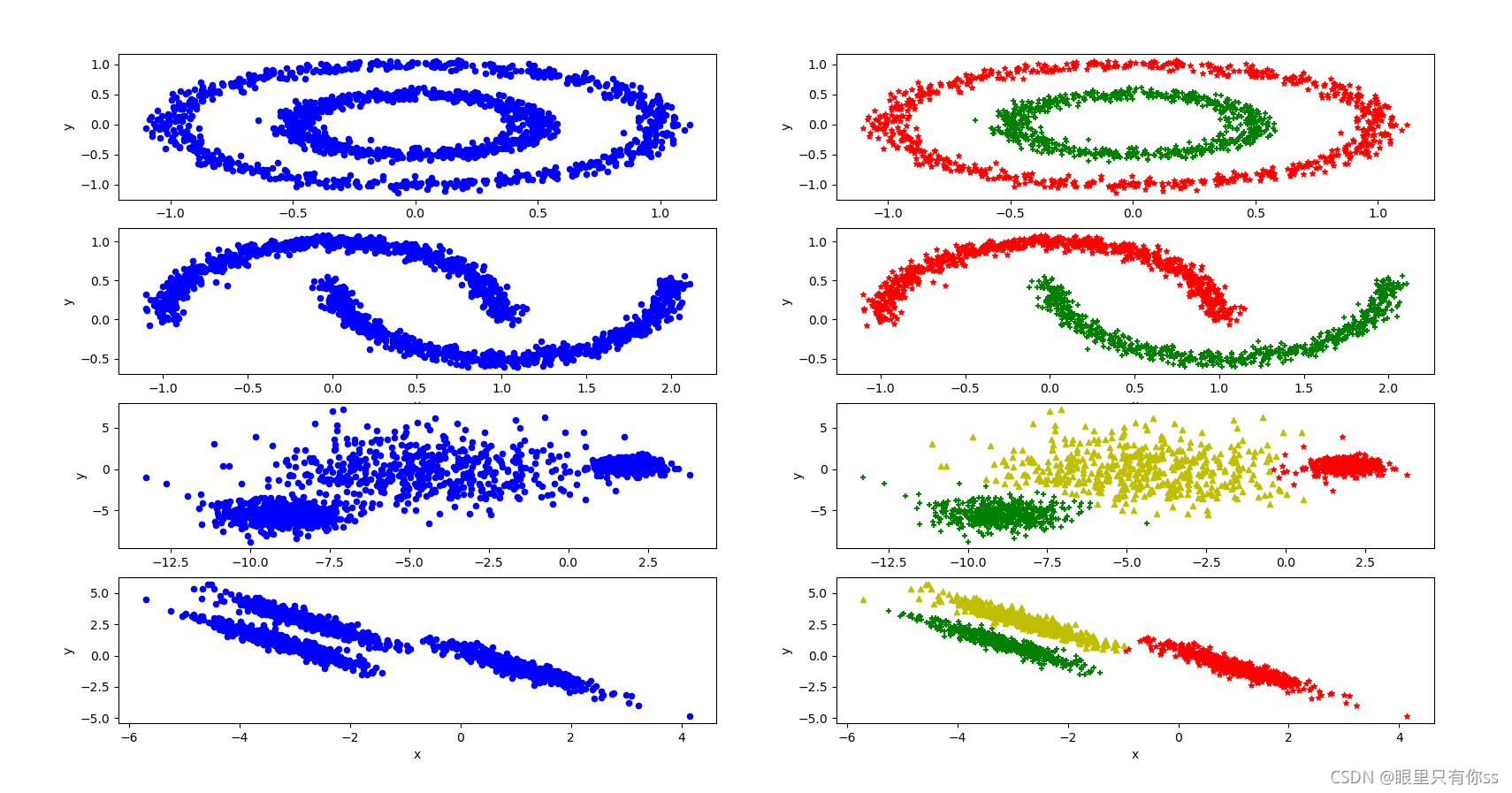
代码比较清晰,数据集参考KMeans的文章,自行下载