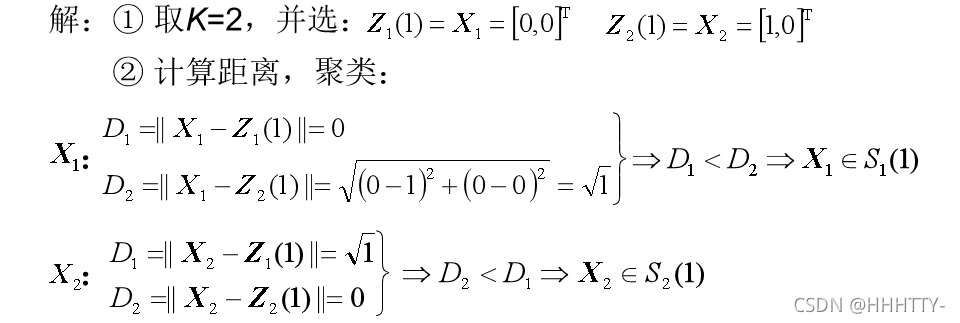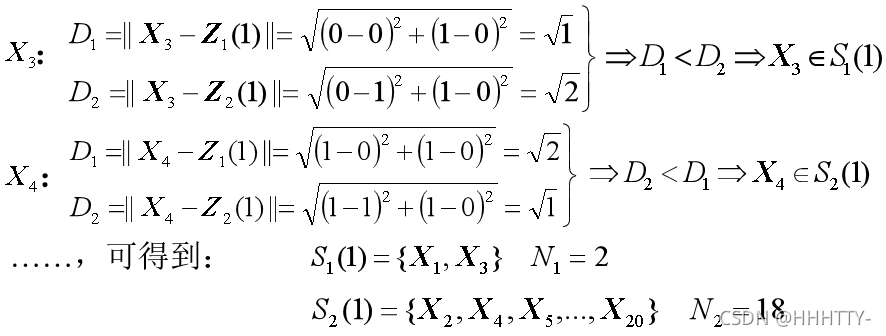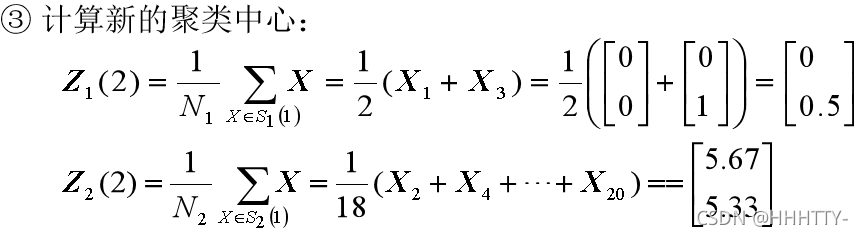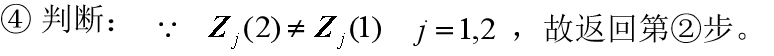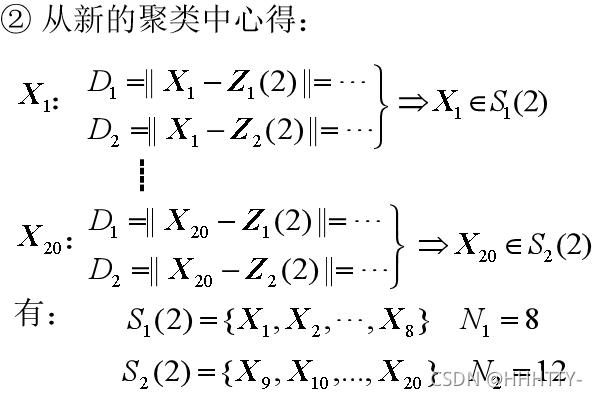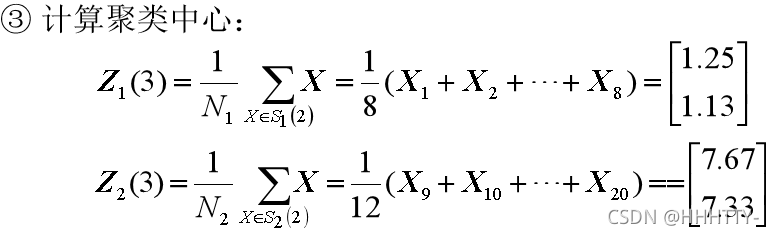目录
动态聚类法
两种常用算法:
- K-均值算法(K-means算法)
- 迭代自组织的数据分析算法(ISODATA, iterative self-organizing data analysis techniques algorithm)
?
一、K—均值算法(K-means)
1.1 条件及约定
- 设待分类的模式特征矢量集为 { x1,x2,…,xN };
- 类的数目K是事先取定的。
1.2 基本思想:
- 首先任意选取K个聚类中心
- 按最小距离原则将各模式分配到K类的某一类;
- 不断计算聚类中心和调整各模式的类别
- 最终使各模式到其判属类别中心的距离平方之和最小。
1.3 基于使聚类准则函数最小化
准则函数
- 聚类集中每一样本点到该类中心的距离平方和。
对于第 j 个聚类集,准则函数定义为
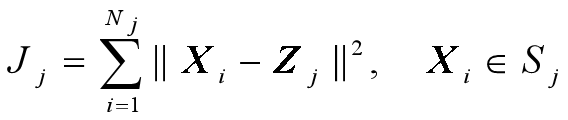
- Sj:第j个聚类集(域),
- 聚类中心为Zj;
- Nj:第j个聚类集Sj中所包含的样本个数。
?
?
对所有K个模式类有:
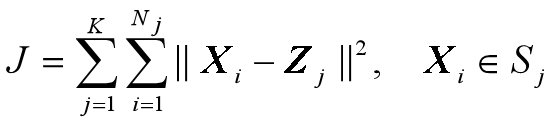
?
?
聚类准则
K-均值算法的聚类准则:
- 聚类中心的选择应使准则函数J极小
- 即使Jj的值极小。
?
对于某一个聚类 j:
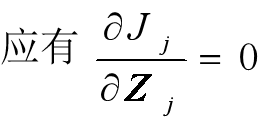
即 :
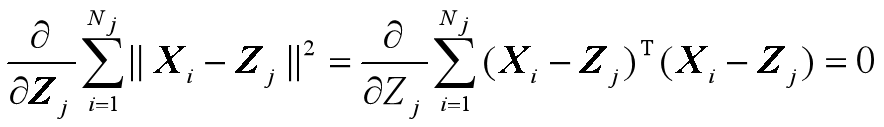
可解得 :
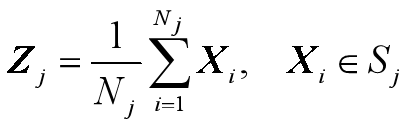
1.4 算法步骤
(1) 任选K个模式特征矢量作为初始聚类中心:
- z1(1) ,z2(1) ,…zK(1)。
- 括号内的序号表示迭代次数
(2) 将待分类的模式特征矢量集{x}中的模式
- 逐个按最小距离原则分划给K类中的某一类。
- 如果
D
j
(
k
)
=
min
?
{
∥
x
?
Z
i
(
k
)
∥
}
,
i
=
1
,
2
,
…
,
K
\mathrm{D}_{j}(k)=\min \left\{\left\|x-\mathrm{Z}_{i}(k)\right\|\right\}, \quad i=1,2, \ldots, K
Dj?(k)=min{∥x?Zi?(k)∥},i=1,2,…,K
则判 x ∈ S j ( k ) x \in S_{j}(k) x∈Sj?(k)
(3) 计算重新分类后的各聚类中心 z j ( k + 1 ) z_{j}(k+1) zj?(k+1)
- 即 求各聚类域中所包含样本的均值向量:
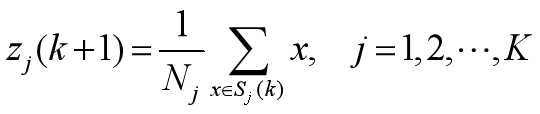
- 以均值向量作新的聚类中心,
- 可得新的准则函数:
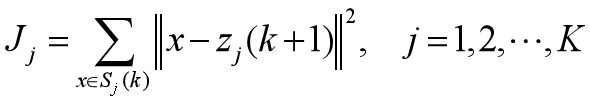
- 可得新的准则函数:
(4) 如果 z j ( k + 1 ) = z j ( k ) ( j = 1 , 2 , … K ) z_{j}(k+1)=z_{j}(k)(j=1,2, \ldots K) zj?(k+1)=zj?(k)(j=1,2,…K),则结束;
- 否则,k=k+1, 转(2)
?
1.5 讨 论
-
“动态”聚类法?
- 聚类过程中,
聚类中心位置或个数发生变化。
?
- 聚类过程中,
-
算法讨论
结果受到:
1. 所选聚类中心的个数和其初始位置
2. 以及模式样本的几何性质及读入次序等的影响实际应用中需要试探不同的K值和选择不同的聚类中心起始值。
?
1.6 例题
例2.3:已知20个模式样本如下,试用K-均值算法分类。
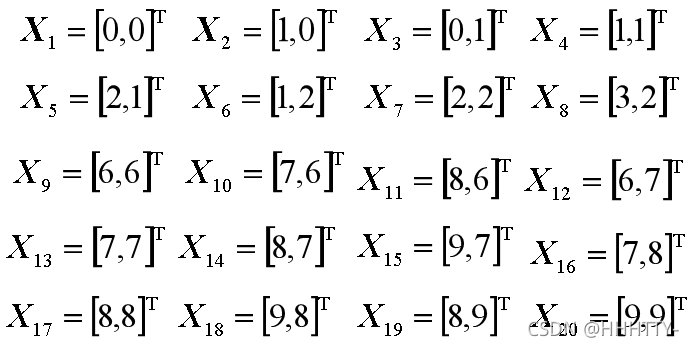
解:
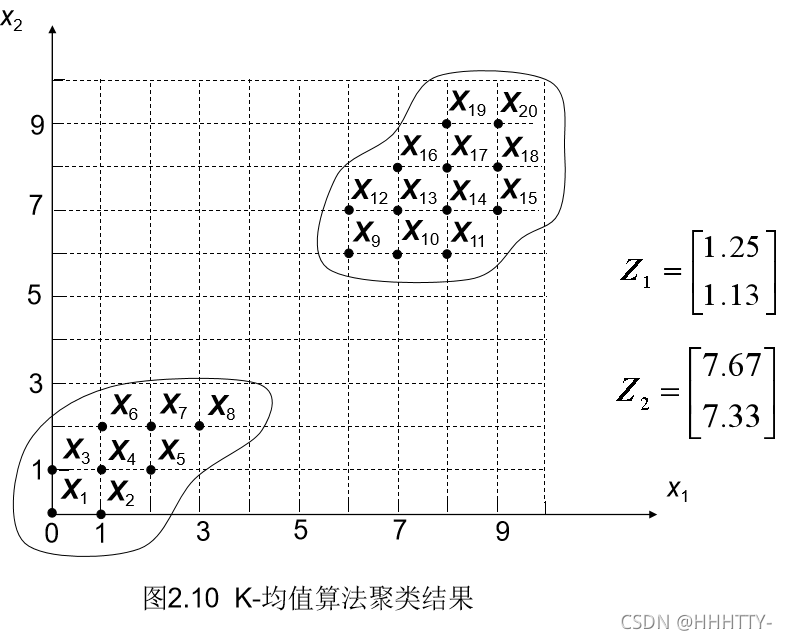
结果图示:
?
?
?
1.7 类别数目未知情况下如何使用?
- 在类别数未知情况下使用K—均值算法时:
- 可以假设类别数是逐步增加的。
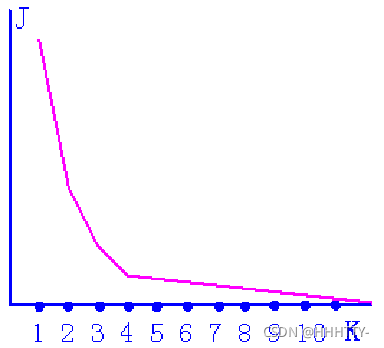
- 显然准则函数是随K的增加而单调地减少的。
?
- 如果样本集的合理聚类数为K类
- 当类别数从1增加到K时准则函数迅速减小
- 当类别数超过K时,准则函数虽然继续减少但会呈现平缓趋势。
1.8 如何避免初始聚类中心的影响?
-
多次运行K均值算法
例如50~1000次,每次随机选取不同的初始聚类中心。
-
聚类结束后计算准则函数值。
-
选取准则函数值最小的聚类结果为最后的结果。
-
该方法一般适用于聚类数目小于10的情况。
?
?
?
二、ISODATA算法
2.1 ISODATA算法的提出
(iterative self-organizing data analysis techniques algorithm,ISODATA)
- K—均值算法比较简单,但它的自我调整能力也比较差。
- 这主要表现在类别数不能改变
- 受代表点初始选择的影响也比较大。
ISODATA算法的功能与K—均值算法相比,在下列几方面有改进:
-
可以改变类别数目。
通过类别的合并与分裂来实现。 -
合并
· 主要发生在某一类内样本个数太少的情况
· 或两类聚类中心之间距离太小的情况。
· 为此设有最小类内样本数限制,以及类间中心距离参数。 -
分裂
· 主要发生在某一类别的某分量出现类内方差过大的现象
· 因而宜分裂成两个类别,以维持合理的类内方差。
· 给出一个对类内分量方差的限制参数,用以决定是否需要将某一类分裂成两类。 -
由于算法有自我调整的能力
· 因而需要设置若干个控制用参数。
· 如:
聚类数期望值K
每次迭代允许合并的最大聚类对数L
允许迭代次数I
?
2.2 ISODATA算法
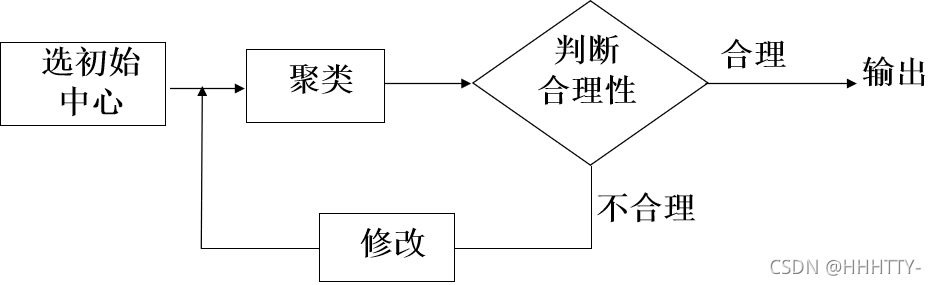
2.2.1基本步骤和思路
-
(1) 选择初始控制参数。
可选不同的指标,也可在迭代过程中人为修改,
以将N个模式样本按指标分配到各个聚类中心中去。 -
(2) 计算各类中诸样本的距离指标函数。
-
(3)~(5)按给定的要求,将前一次获得的聚类集进行分裂和合并处理
【(4)为分裂处理,(5)为合并处理 】
从而获得新的聚类中心。 -
(6) 重新进行迭代运算
计算各项指标
判断聚类结果是否符合要求,如不符合,返回(2)。
经过多次迭代后,若结果收敛,则运算结束。