[人工智能] 机器学习实验三（决策树）

?决策树学习的关键在于如何选择最优的划分属性，所谓的最优划分属性，对于二元分类而言，就是尽量使划分的样本属于同一类别，即“纯度”最高的属性。那么如何来度量特征（features）的纯度，这时候就要用到“信息熵（information entropy）”。先来看看信息熵的定义：假如当前样本集D中第k类样本所占的比例为，为类别的总数（对于二元分类来说，）。则样本集的信息熵为：

Ent(D)的值越小，则D的纯度越高。（这个公式也决定了信息增益的一个缺点：即信息增益对可取值数目多的特征有偏好（即该属性能取得值越多，信息增益，越偏向这个），因为特征可取的值越多，会导致“纯度”越大，即ent（D）会很小，如果一个特征的离散个数与样本数相等，那么Ent（D）值会为0）。再来看一个概念信息增益（information gain），假定离散属性 ?有个可能的取值，如果使用特征 ?来对数据集D进行划分，则会产生V个分支结点，其中第v（小v）个结点包含了数据集D中所有在特征 ?上取值为的样本总数，记为。因此可以根据上面信息熵的公式计算出信息熵，再考虑到不同的分支结点所包含的样本数量不同，给分支节点赋予权重，即样本数越多的分支节点的影响越大，因此，能够计算出特征 ?对样本集D进行划分所获得的“信息增益”:

? ? ? ?一般而言，信息增益越大，则表示使用特征 ?对数据集划分所获得的“纯度提升”越大。所以信息增益可以用于决策树划分属性的选择，其实就是选择信息增益最大的属性，ID3算法就是采用的信息增益来划分属性。
?

三、ID3算法

1、算法简介

ID3算法（Iterative Dichotomiser 3）是一种基于信息熵的决策树分类学习算法，以信息增益和信息熵作为对象分类的衡量标准，该算法的核心是在决策树各级节点上选择属性时，用信息增益作为属性的选择标准，使得在每一个非节点进行测试时，能获得关于被测试记录最大的类别信息。

2、数据收集

本次实验所采用的数据来自UCI数据集，数据集题目为群众对汽车各种因素的接受情况。如图：

其中，前五列为标签分别为：buying,maint,doors,persons,lug_boot,safty,最后一个为决策结果，unacc表示无法接受，acc表示接受，good表示?很好，vgood表示非常好

数据加载

def loadData(dataseturl):
    dataset = []
    with open(dataseturl) as f:
        dataall = f.readlines()
    for data in dataall:
        dataline = data.strip().split(',')
        dataset.append(dataline)
    #六个属性
    labels=['buying','maint','doors','persons','lug_boot','safty']
    return dataset,labels

计算给定数据的香农熵

def calShannonEnt(dataset):
    numEntries = len(dataset)
    labelCounts={}
    for data in dataset:
        #提取标签信息
        classlabel = data[-1]
        if(classlabel not in labelCounts.keys()):
            labelCounts[classlabel]=0
        labelCounts[classlabel]+=1
    shannonEnt=0.0
    for key in labelCounts:
        p = float(labelCounts[key])/numEntries
        shannonEnt-= p*np.log2(p)
    return shannonEnt

根据某一特征划分数据集

def splitDataset(dataset,axis,value):#axis 属性的位置 value 返回数据属性值为value
    retDataSet = []
    for featVec in dataset:
        if featVec[axis]==value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

选择最佳属性划分数据集

def chooseBestFeatureToSplit(dataset):
    numFeatures = len(dataset[0])-1 #计算特征数
    baseEntropy = calShannonEnt(dataset)#计算信息熵
    bestFeature = -1
    bestInfoGain = 0
    for i in range(numFeatures): #不断循环属性
        featList = [example[i] for example in dataset] #获取数据集的第i个特征
        uniqueVals = set(featList) #属性i的属性值有哪些
        newEntropy = 0.0
        for value in uniqueVals:#
            subDataSet = splitDataset(dataset,i,value) #按照属性i和属性i的值value进行数据划分
            prob = len(subDataSet)/float(len(dataset))
            newEntropy +=prob*calShannonEnt(subDataSet) #计算划分过数据集的信息熵
        infoGain = baseEntropy-newEntropy #计算信息增益，也就是信息熵的变换量
        print("第%d个特征的信息增益为：%.3f" % (i, infoGain))
        if(infoGain>bestInfoGain):
            bestInfoGain = infoGain
            bestFeature=i
    return bestFeature

若所有属性使用完毕后，类标签还无法统一，使用投票的方式进行统一

def majorityCnt(classList):
    classCount={ }
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote]=0
        else:
            classCount[vote]+=1
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

创建并递归遍历该棵树

def createTree(dataset,labels):#数据集和标签列表
    classList =[example[-1] for example in dataset]#数据所属类得值
    if classList.count(classList[0])==len(classList):#条件1：classList只剩下一种值
        return classList[0]
    if len(dataset[0])==1:#条件2：数据dataset中属性已使用完毕，但没有分配完毕
        return majorityCnt(classList)#取数量多的作为分类
    bestFeat = chooseBestFeatureToSplit(dataset)#选择最好的分类点，即香农熵值最小的
    labels2 = labels.copy()#复制一分labels值，防止原数据被修改。
    bestFeatLabel = labels2[bestFeat]
    myTree = {bestFeatLabel:{}}#选取获取的最好的属性作为
    del(labels2[bestFeat])#这里写博客的时候，需要说一下关于list值得变化
    featValues = [example[bestFeat] for example in dataset]#获取该属性下的几类值
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels2[:]#剩余属性列表
        myTree[bestFeatLabel][value] = createTree(splitDataset(dataset,bestFeat,value),subLabels)
    return myTree
# 进行分类---通过递归方式对这颗树进行遍历
def classify(inputTree, featLabels, testVec):
    firstStr = list(inputTree.keys())[0]
    secondDic = inputTree[firstStr]  # 获取最外层字典里的值
    featIndex = featLabels.index(firstStr)  # 获取最外层属性值在属性列表中的位置
    try:
        for key in secondDic.keys():
            if testVec[featIndex] == key:
                if isinstance(secondDic[key], dict):
                    classLabel = classify(secondDic[key], featLabels, testVec)
                else:
                    classLabel = secondDic[key]
        return classLabel
    except:
        secondDic[key]

存储树并且加载

#存储树（以二进制序列化进行存储）
def storeTree(inputTree,filename):
    fw = open(filename,'wb')
    pickle.dump(inputTree,fw)
    fw.close()
#加载存储的树  以二进制返回加载的序列化值
def grabTree(filename):
    fr = open(filename,'rb')
    return pickle.load(fr)

添加主函数运行代码

if __name__ == '__main__':
    dataSet, labels = loadData('cardata.txt')
    print("数据集信息熵："+str(calShannonEnt(dataSet)))
    print("最优索引值："+str(chooseBestFeatureToSplit(dataSet)))
    mytree = createTree(dataSet,labels)
    filename = 'testdata.txt'
    storeTree(mytree,filename)
    tree = grabTree(filename)
    print("加载出来的tree:",tree)
    print("输出mytree的key:",list(mytree.keys())[0])
    treePlotter.createPlot(mytree)

运行结果

使用测试集数据测试训练模型

if __name__ == '__main__':
    dataSet, labels = loadData('carData.txt')
    # print("数据集信息熵："+str(calShannonEnt(dataSet)))
    # print("最优划分属性索引值："+str(chooseBestFeatureToSplit(dataSet)))
    mytree = createTree(dataSet, labels)
    testDataset = loadtestData("testData.txt")
    count=0
    for dataset in testDataset:
        result = classify(mytree,labels,dataset[:6])
        print("测试结果为：{}，标准结果为：{}".format(result,dataset[6]))
        if(result==dataset[6]):
            count+=1
    print("正确率：%f"%(count/84))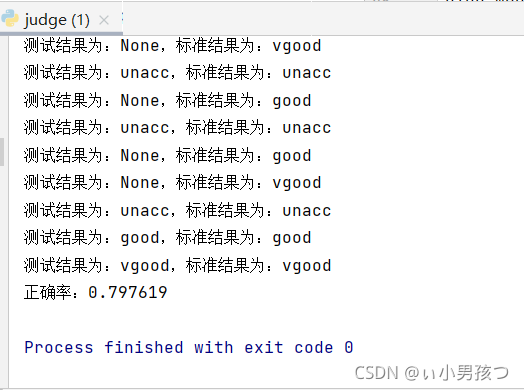

总结：?

ID3优点：理论清晰，方法简单，学习能力较强

? ? 缺点：(1) 信息增益的计算比较依赖于特征数目比较多的特征
????(2) ID3为非递增算法
????(3) ID3为单变量决策树
????(4) 抗糙性差?

C4.5算法

信息增益率

ID3算法中的信息增益准则对取值数目较多的属性有所偏好，例如西瓜数据集中，如果把“编号”也作为候选划分属性，它的信息增益为0.998，但是如果用“编号”作为划分属性显然是不合理的。为了减少这种偏好可能带来的不利影响，C4.5决策树算法中使用增益率（gain ratio）来选择最优划分属性。

IV(a)称为属性a的固有值，属性a的可能取值数目越多，则IV(a)的值通常会越大。因此，增益率准则对可取值数目较少的属性有所偏好，因此，C4.5算法并不是直接选择增益率最大的候选划分属性，而是先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

C4.5算法优点

C4.5算法较之ID3算法主要有4点改进：

采用信息增益率作为最优划分属性。
能够处理连续值类型的属性。
能够处理缺失值属性。
增加了剪枝处理，从而避免过拟合。

C4.5算法实现

更改ID3的局部函数，将

for value in uniqueVals:
    #按照属性i和属性i的值value进行数据划分
    subDataSet = splitDataset(dataset,i,value)
    prob = len(subDataSet)/float(len(dataset))
    newEntropy +=prob*calShannonEnt(subDataSet) #计算划分过数据集的信息熵
infoGain = baseEntropy-newEntropy #计算信息增益，也就是信息熵的变换量

改为

for value in uniqueVals:
    #按照属性i和属性i的值value进行数据划分
    subDataSet = splitDataset(dataset,i,value)
    prob = len(subDataSet)/float(len(dataset))
    newEntropy +=prob*calShannonEnt(subDataSet) #计算划分过数据集的信息熵
    splitInfo -= prob*np.log2(prob)
infoGain = (baseEntropy-newEntropy)/splitInfo  #求出第i列属性的信息增益率

由运行结果准确率可以看出，C4.5算法划分策略比ID3更好。

基尼指数

基尼指数定义：

基尼指数实例

基尼指数的代码实现

    # 计算某一维度相对于标签的基尼指数
    def Gini(self, y):
        size = len(y) # 数据集大小
        gini_total = 0
        classes_idx_num = dict(Counter(y)) # 统计每类标签下包含的数据个数
        # 计算基尼系数:
        for key in classes_idx_num.keys():
            # 计算第key个标签的基尼系数分量
            prob = classes_idx_num[key] / size # 用出现频率表示概率
            gini_total += prob * prob
        return 1 - gini_total


    '''划分选择:使用基尼系数'''
    # X:     输入数据, size=(batches, features)
    # y:     类别标签, size=(batches,)
    # dim:   当前是第几维度
    # num_D: 数据总数
    def GiniIdx(self, X, y, num_D, dim):
        a = X[:, dim] # 获取数据第dim维度
        v = set(a)    # 获取数据第dim维度可能的取值
        gini_a = 0
        # 计算数据第dim维度的信息增益:
        for i in v:
            # 第dim维度第i个取值出现的频率
            prob_a_v = np.sum(a==i)/num_D
            gini_a_v = self.Gini(y[np.where(a==i)])
            gini_a += prob_a_v * gini_a_v
        return gini_a