梯度下降算法
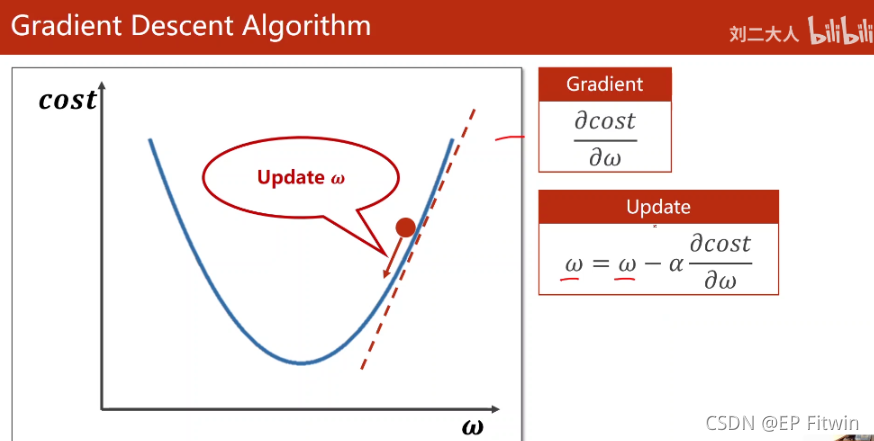
对w向梯度的负方向更新,α表示学习率,这样可使得每次都朝着下降最快的方向移动。

梯度下降对于非凸函数只能找到局部最优,很难找到全部最优(没有一个点的函数值比它小的点)

对线性损失函数进行梯度下降(求导w)代码:
代码
import matplotlib.pyplot as plt
# prepare the training set
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# initial guess of weight
w = 1.0
# define the model linear model y = w*x
def forward(x):
return x*w
# define the cost function MSE
def cost(xs, ys):
cost = 0
for x, y in zip(xs, ys):
y_pred = forward(x)
cost += (y_pred - y) ** 2
return cost / len(xs)
# define the gradient function gd
'''
如何找到梯度下降的方向:用目标函数对权重w求导数可找到梯度的变化方向
'''
def gradient(xs, ys):
grad = 0
for x, y in zip(xs, ys):
grad += 2*x*(x*w - y)
return grad / len(xs)
epoch_list = []
cost_list = []
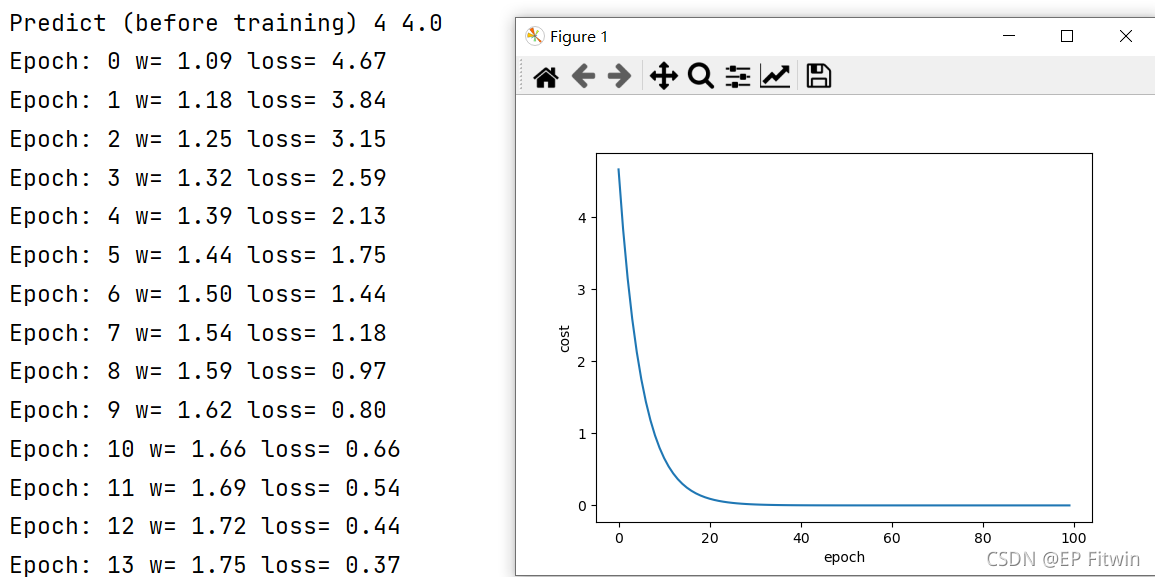
print("Predict (before training)", 4, forward(4))
for epoch in range(100):
# 计算损失值
cost_val = cost(x_data, y_data)
# 计算梯度变化值
grad_val = gradient(x_data, y_data)
w -= 0.01 * grad_val
print('Epoch:', epoch, "w=", "%.2f" %w, "loss=", "%.2f" %cost_val)
epoch_list.append(epoch)
cost_list.append(cost_val)
print("Predict (after training)", 4, forward(4))
plt.plot(epoch_list, cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()
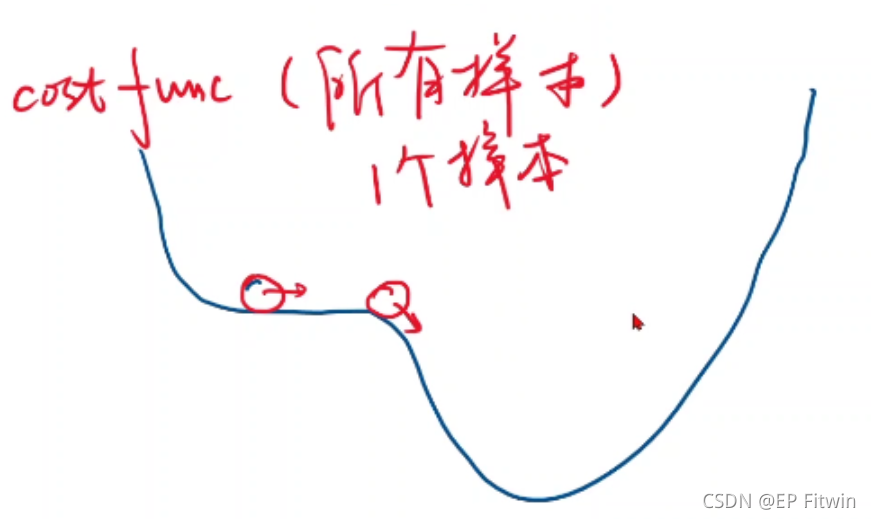
随机梯度下降算法:

从N个数据中随机选一个,用单个样本的损失loss对权重求导,然后进行求导。(随机取得样本有可能帮助我们跨越鞍点,向最优值前进)。更新公式也只需要对一个样本求导了。
代码:
import matplotlib.pyplot as plt
# prepare the training set
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# initial guess of weight
w = 1.0
# define the model linear model y = w*x
def forward(x):
return x * w
# define the cost function MSE
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
# define the gradient function gd
'''
如何找到梯度下降的方向:用目标函数对权重w求导数可找到梯度的变化方向
'''
def gradient(x, y):
return 2 * x * (x * w - y)
epoch_list = []
loss_list = []
print("Predict (before training)", 4, forward(4))
# 对每一个样本的梯度进行更新
for epoch in range(100):
for x, y in zip(x_data, y_data):
loss_val = loss(x, y)
grad_val = gradient(x, y)
w = w - 0.01 * grad_val
print("Epoch: ", epoch, "w: ", "%.2lf"%w, "loss: ", "%.2lf"%loss_val)
epoch_list.append(epoch)
loss_list.append(loss_val)
print("Predict (after training)", 4, forward(4))
plt.plot(epoch_list, loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()
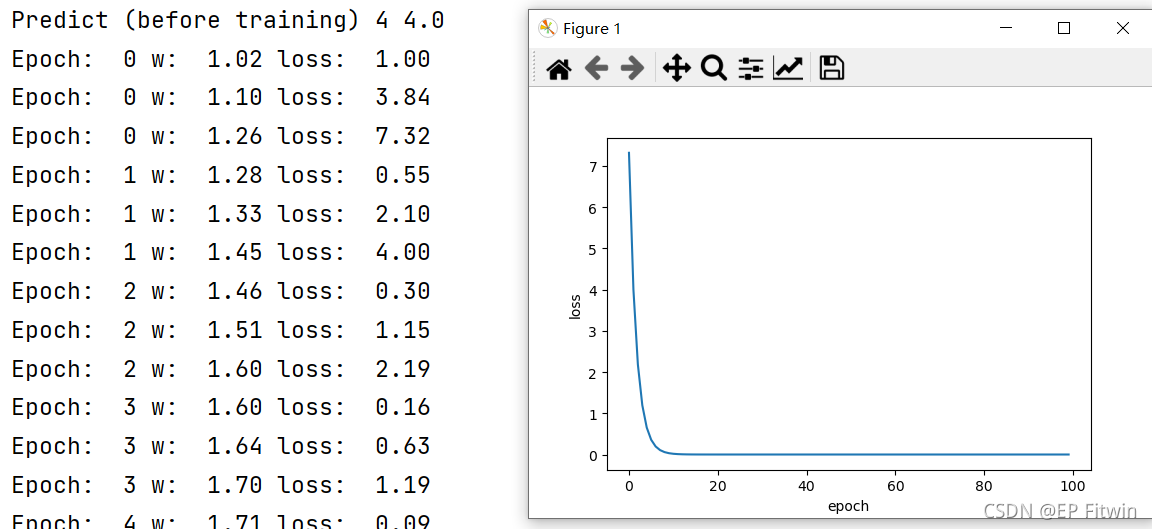
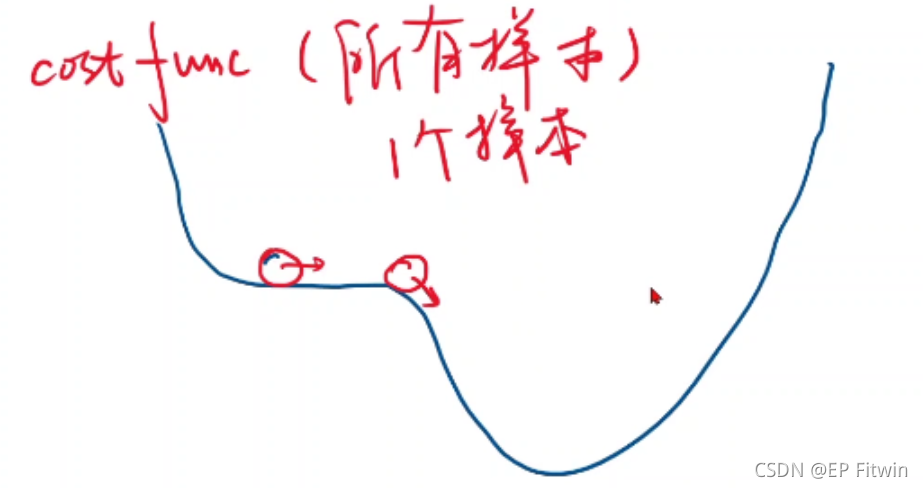
随机梯度下降法和梯度下降法的主要区别在于:
1、损失函数由cost()更改为loss()。cost()是计算所有训练数据的损失,loss()是计算一个训练函数的损失。对应于源代码则是少了两个for循环。
2、梯度函数gradient()由计算所有训练数据的梯度更改为计算一个训练数据的梯度。
3、本算法中的随机梯度主要是指,每次拿一个训练数据来训练,然后更新梯度参数。本算法中梯度总共更新100(epoch)x3 = 300次。梯度下降法中梯度总共更新100(epoch)次。
综合梯度下降和随机梯度下降的算法,折中:batch(mini-batch)
说在最后的话:编写实属不易,若喜欢或者对你有帮助记得点赞 + 关注或者收藏哦~