简介
2021年华为杯研赛B题“空气质量预报二次建模”第四题的数据预处理过程用到了一个反距离权重插值(见章节2.1),在这里整理一下。
目录
1. 赛题及数据
1.1 竞赛试题
? ? ? ? ?完整赛题及数据大家可自行前往“中国研究生创新实践系列大赛管理平台”下载,或者直接在网上搜索。 这里仅展示问题4。
? ? ? ? 问题4. 相邻区域的污染物浓度往往具有一定的相关性,区域协同预报可能会提升空气质量预报的准确度。如图 4,监测点A的临近区域内存在监测点A1、A2、A3,使用附件1、3中的数据,建立包含A、A1、A2、A3四个监测点的协同预报模型,要求二次模型预测结果中AQI预报值的最大相对误差应尽量小,且首要污染物预测准确度尽量高。使用该模型预测监测点A、A1、A2、A3在2021年7月13日至7月15日6种常规污染物的单日浓度值,计算相应的AQI和首要污染物,将结果依照附录“污染物浓度及AQI预测结果表”的格式放在论文中。并讨论:与问题3的模型相比,协同预报模型能否提升针对监测点A的污染物浓度预报准确度?说明原因。

1.2 数据集预览
官方提供数据集如下,问题4预处理过程只需用到附件1、附件3数据。
附件1 监测点A空气质量预报基础数据
附件2 监测点B、C空气质量预报基础数据
附件3?监测点A1、A2、A3空气质量预报基础数据?
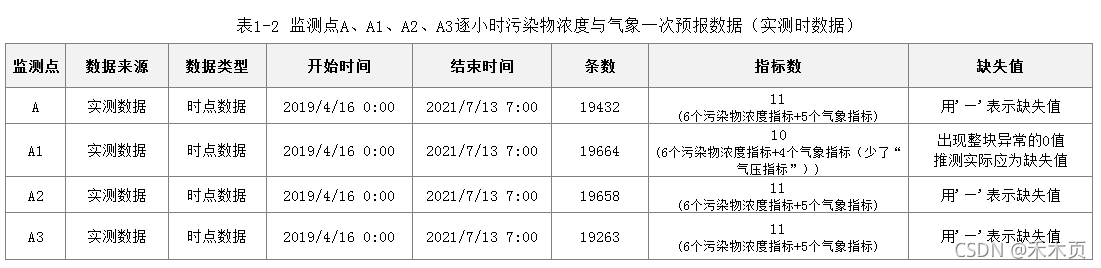
从附件名字可以推测数据集的内部结构应该基本一致,只是监测点不同而已,事实也是如此。以监测点A为例,表1-1展示了监测点A提供的三份数据。

? ? ? ? 参考博主另一篇文章《[Python]数据预处理例题:2021华为杯数学建模B题“空气质量预报二次建模”》,会知道:
? ? ? ?对于sheet1,由于一次预报数据不知道是原来就预报不正确,还是由于后期记录或抄写出现的错误,而题目本就要求改进一次预报模型,如果是原模型就不正确那我们给他更正也没有道理,因此对sheet1预处理工作仅了解缺失日期情况,不做进一步处理。
? ? ? 对于sheet3,其实它跟sheet2是差不多,只是一个是时数据,一个是日数据。通过一些简单的探索分析,能够发现除O3外,sheet3中的数据几乎都是sheet2中对应日期的24h平均;O3的计算方式是取sheet2对应日期的“8小时滑动平均的最大值”,因此sheet3的预处理建立在sheet2之上。
? ? ? 综上,协同处理部分只对监测点A、A1、A2、A3的sheet2"监测点A逐小时污染物浓度与气象实测数据"(以下简称“实测时数据”)处理就好。
?以下数据处理均在Spyder3.7中进行。
import os
import pandas as pd
import numpy as np
#设置工作目录
os.chdir('C:\\Users\...)
os.getcwd()
#监测点A、A1、A2、A实测时数据导入
df2A=pd.read_excel("附件1 监测点A空气质量预报基础数据.xlsx","监测点A逐小时污染物浓度与气象实测数据")
df2A1=pd.read_excel("附件3 监测点A1、A2、A3空气质量预报基础数据.xlsx","监测点A1逐小时污染物浓度与气象实测数据")
df2A2=pd.read_excel("附件3 监测点A1、A2、A3空气质量预报基础数据.xlsx","监测点A2逐小时污染物浓度与气象实测数据")
df2A3=pd.read_excel("附件3 监测点A1、A2、A3空气质量预报基础数据.xlsx","监测点A3逐小时污染物浓度与气象实测数据")2. 监测点A、A1、A2、A3实测时数据协同处理
2.1 缺失值处理1:反向距离权重
由于题目说到:监测点A、A1、A2、A3存在协同作用,即它们之间的变量可能存在一定的相关性。又考虑到污染物浓度和气象条件在地表上应当是连续变化的,所以在缺失值处理时,可以引入反向距离权重,对于缺失的数据,用其他2-3个监测点的反向距离权重进行加权。
插值的数学表达式为:
?令dij表示监测点i和监测点j之间的欧式距离,权重表达式为:
?此处取:
?根据坐标生成距离权重的代码如下所示:
#定义计算欧氏距离函数
def distEclud(vecA, vecB):
return np.sqrt(np.sum(np.power((vecA - vecB), 2)))
#导入四个监测点坐标
vecA=np.array([0,0])
vecA1=np.array([-14.4846,-1.9699])
vecA2=np.array([-6.6716,7.5953])
vecA3=np.array([-3.3543, -5.0138])
#监测点A、A1、A2、A3之间的反向距离权重
w01=1/distEclud(vecA,vecA1)
w02=1/distEclud(vecA,vecA2)
w03=1/distEclud(vecA,vecA3)
w12=1/distEclud(vecA1,vecA2)
w13=1/distEclud(vecA1,vecA3)
w23=1/distEclud(vecA2,vecA13)
#创建权重矩阵
W=np.array([[0,w01,w02,w03],[0,0,w12,w13],[0,0,0,w23],[0,0,0,0]]);W
Out[8]:
array([[0. , 0.0684091 , 0.09891839, 0.16577225],
[0. , 0. , 0.08096807, 0.0866625 ],
[0. , 0. , 0. , 0.07669788],
[0. , 0. , 0. , 0. ]])
#形成对称矩阵(此处对角线元素为零,后面不减也是可以的)
W += W.T - np.diag(W.diagonal());W
Out[9]:
array([[0. , 0.0684091 , 0.09891839, 0.16577225],
[0.0684091 , 0. , 0.08096807, 0.0866625 ],
[0.09891839, 0.08096807, 0. , 0.07669788],
[0.16577225, 0.0866625 , 0.07669788, 0. ]])用反向距离权重加权的处理的思路是:
步骤1:把监测点A、A1、A2、A3实测时数据按变量拆分成11个数据集
步骤2:在每个数据集中依次找出每一列缺失值的位置
步骤3:判断缺失值类型,如果除了要插值的位置,还有至少两个点位是非缺失的,就进行反向距离权重插值。(这里强调“至少两个点位时非缺失”的是因为:如果所有点位缺失,肯定无法实现插值;如果仅一个点位非缺失,那么插值结果就等于非缺失的那个值,意义不大)
步骤4:最后将数据恢复成原来A、A1、A2、A3的样子。
以变量“气压(MBar)”为例,下文函数中出现的【df】数据集格式如下,从左到右依次为监测点A、A1、A2、A3的气压值。
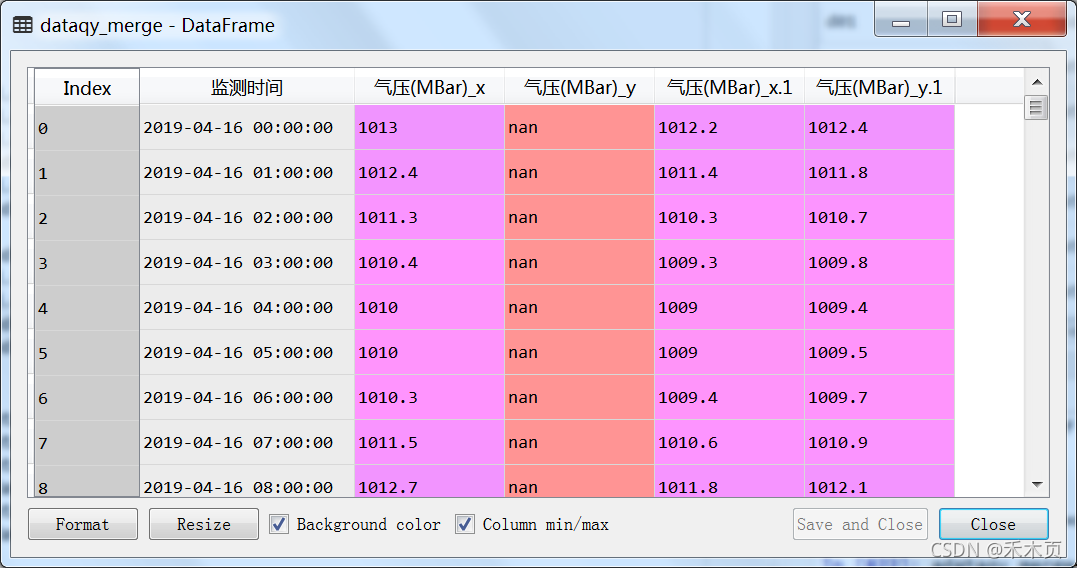
?图1 数据集重组格式
2.1.1 反向距离权重函数定义方法一
方法一依次处理每一列数据,完全按照上述逻辑。
优点是代码好理解,运行速度也比较快。缺点代码较长,且与这份数据完全匹配,增加或减少一个监测点就需要全部重写。
#定义一个函数,实现反距离权重插值
def cov_nan(df):
#对第监测点A数据作处理
loca_nan1=np.where(pd.isna(df.iloc[:,1]))[0] #获取缺失值所在的行
for i in loca_nan1:
if (df.iloc[i,2]!=np.nan) & (df.iloc[i,3]!=np.nan) & (df.iloc[i,4]!=np.nan): #都不缺失
df.iloc[i,1]=w01/(w01+w02+w03)*df.iloc[i,2]+w02/(w01+w02+w03)*df.iloc[i,3]+w03/(w01+w02+w03)*df.iloc[i,4]
if (df.iloc[i,2]==np.nan) & (df.iloc[i,3]!=np.nan) & (df.iloc[i,4]!=np.nan): #2缺失
df.iloc[i,1]=w02/(w02_w03)*df.iloc[i,3]+w03/(w02_w03)*df.iloc[i,4]
if (df.iloc[i,2]!=np.nan) & (df.iloc[i,3]==np.nan) & (df.iloc[i,4]!=np.nan): #3缺失
df.iloc[i,1]=w01/(w01+w03)*df.iloc[i,2]+w03/(w01+w03)*df.iloc[i,4]
if (df.iloc[i,2]!=np.nan) & (df.iloc[i,3]!=np.nan) & (df.iloc[i,4]==np.nan): #4缺失
df.iloc[i,1]=w02/(w02+w03)*df.iloc[i,3]+w03/(w02+w03)*df.iloc[i,4]
else:
continue
#对第监测点A1数据作处理
loca_nan2=np.where(pd.isna(df.iloc[:,2]))[0]
for i in loca_nan2:
if (df.iloc[i,1]!=np.nan) & (df.iloc[i,3]!=np.nan) & (df.iloc[i,4]!=np.nan): #都不缺失
df.iloc[i,2]=w01/(w01+w12+w13)*df.iloc[i,1]+w12/(w01+w12+w13)*df.iloc[i,3]+w13/(w01+w12+w13)*df.iloc[i,4]
if (df.iloc[i,1]==np.nan) & (df.iloc[i,3]!=np.nan) & (df.iloc[i,4]!=np.nan): #1缺失,3,4
df.iloc[i,2]=w12/(w12+w13)*df.iloc[i,3]+w13/(w12+w13)*df.iloc[i,4]
if (df.iloc[i,1]!=np.nan) & (df.iloc[i,3]==np.nan) & (df.iloc[i,4]!=np.nan): #3缺失,1,4
df.iloc[i,2]=w01/(w01+w13)*df.iloc[i,2]+w13/(w01+w13)*df.iloc[i,4]
if (df.iloc[i,1]!=np.nan) & (df.iloc[i,3]!=np.nan) & (df.iloc[i,4]==np.nan): #4缺失,1,3
df.iloc[i,2]=w01/(w01+w12)*df.iloc[i,1]+w12/(w01+w12)*df.iloc[i,3]
else:
continue
#对第监测点A2数据作处理
loca_nan3=np.where(pd.isna(df.iloc[:,3]))[0]
for i in loca_nan3:
if (df.iloc[i,1]!=np.nan) & (df.iloc[i,2]!=np.nan) & (df.iloc[i,4]!=np.nan): #都不缺失
df.iloc[i,3]=w02/(w02+w12+w23)*df.iloc[i,1]+w12/(w02+w12+w23)*df.iloc[i,2]+w23/(w02+w12+w23)*df.iloc[i,4]
if (df.iloc[i,1]==np.nan) & (df.iloc[i,2]!=np.nan) & (df.iloc[i,4]!=np.nan): #1缺失,2,4
df.iloc[i,3]=w12/(w12+w23)*df.iloc[i,2]+w23/(w12+w23)*df.iloc[i,4]
if (df.iloc[i,1]!=np.nan) & (df.iloc[i,2]==np.nan) & (df.iloc[i,4]!=np.nan): #2缺失,1,4
df.iloc[i,3]=w02/(w02+w23)*df.iloc[i,1]+w23/(w02+w23)*df.iloc[i,4]
if (df.iloc[i,1]!=np.nan) & (df.iloc[i,2]!=np.nan) & (df.iloc[i,4]==np.nan): #4缺失,1,2
df.iloc[i,3]=w02/(w02+w12)*df.iloc[i,1]+w12/(w02+w12)*df.iloc[i,2]
else:
continue
#对第监测点A3数据作处理
loca_nan4=np.where(pd.isna(df.iloc[:,4]))[0]
for i in loca_nan4:
df.iloc[i,4]=100
if (df.iloc[i,1]!=np.nan) & (df.iloc[i,2]!=np.nan) & (df.iloc[i,3]!=np.nan): #都不缺失
df.iloc[i,4]=w03/(w03+w13+w23)*df.iloc[i,1]+w13/(w03+w13+w23)*df.iloc[i,2]+w23/(w03+w13+w23)*df.iloc[i,4]
if (df.iloc[i,1]==np.nan) & (df.iloc[i,2]!=np.nan) & (df.iloc[i,3]!=np.nan): #1缺失,2,3
df.iloc[i,4]=w13/(w13+w23)*df.iloc[i,2]+w23/(w13+w23)*df.iloc[i,3]
if (df.iloc[i,1]!=np.nan) & (df.iloc[i,2]==np.nan) & (df.iloc[i,3]!=np.nan): #2缺失,1,3
df.iloc[i,4]=w03/(w03+w23)*df.iloc[i,1]+w23/(w03+w23)*df.iloc[i,3]
if (df.iloc[i,1]!=np.nan) & (df.iloc[i,2]!=np.nan) & (df.iloc[i,3]==np.nan): #3缺失,1,2
df.iloc[i,4]=w03/(w03+w13)*df.iloc[i,1]+w13/(w03+w13)*df.iloc[i,2]
else:
continue
return df
2.1.2?反向距离权重函数定义方法二
函数定义方法二代码的逻辑与之前一致,按步骤1-3进行,但用了权重矩阵W,大致逻辑如下图所示,具体代码如下。
优点是代码更简洁,普适性也更强一些,增加或减少监测点都还能用;缺点是嵌套了两个for循环,运行速度要慢一些。

#定义一个函数,实现反距离权重插值
def cov_nan(df,W):
"""
功能:当除要插值的监测点外,还存在2个及以上其他点位时,实现反向距离权重插值
df格式:第一列为“key”变量,后面依次为A、A1、A2、A3等数据
W格式:与df非“key”变量对应的权重
"""
for col in range(1,df.shape[1]): #对于除“key”变量的每一列
loca_nan=np.where(pd.isna(df.iloc[:,col]))[0] #查看每一列缺失值所在的行
for i in loca_nan:
#切出含有缺失值的行
h=df.iloc[i,1:df.shape[1]]
#定义一个缺失值示性向量
I=np.array(np.repeat(1,df.shape[1]-1))
I[h.isnull()]=0
#除了要插值的变量,至少还有有2个其他点位变量才适合用反距离权重插值
if I.sum()>=2:
W_sum=(W[col-1]*I).sum()
df.iloc[i,col]=(h*W[col-1]*I/W_sum).sum()
else:
continue
return df 2.1.3 协同处理插值
利用反向距离权重插值同时处理监测点A、A1、A2、A3数据时,需要把数据按变量重组成图一的【df】格式,这里先用merge匹配一下数据,再进行拆分。
注意merge中how='outer',取四个数据集“监测时间”的并集,对于有“监测时间”缺失的,也可一并补上。
#步骤1:一些预处理工作
#通过数据预览,发现A1少了“气压变量”,为使数据结构一致,给他补回去
s=np.repeat(np.nan, df2A1.shape[0])
df2A1.insert(10, '气压(MBar)', s)
#通过数据预览,发现监测点A1部分数据为异常的零,实际应判断缺失值
df2A1.iloc[0:5360,8:13]=np.nan
#通过数据预览,发现A、A2、A3存在'—'缺失
df2A=df2A.replace('—',np.nan)
df2A2=df2A2.replace('—',np.nan)
df2A3=df2A3.replace('—',np.nan)
#都删去“地点”
df2A.drop(['地点'],axis=1,inplace=True)
df2A1.drop(['地点'],axis=1,inplace=True)
df2A2.drop(['地点'],axis=1,inplace=True)
df2A3.drop(['地点'],axis=1,inplace=True)
#发现A、A1、A2、A3变量顺序一样,名字也一样
#步骤2:将A、A1、A2、A3实测时数据合并【df_mergeA】
df_mergeA=pd.merge(df2A,df2A1,on='监测时间',how='outer')
df_mergeA=pd.merge(df_mergeA,df2A2,on='监测时间',how='outer')
df_mergeA=pd.merge(df_mergeA,df2A3,on='监测时间',how='outer')
#缺失值替换
df_mergeA=df_mergeA.replace('na',np.nan)
#转化为数值型
df_mergeA.iloc[:,1:45]=df_mergeA.iloc[:,1:45].astype('float64')
#小处理:这里发现,merge完的数据虽然数据量没有太大变化,但spyder预览窗口莫名变得很卡,包括从merge中切片出来的数据
#但是将生成的df_mergeA导出再导入后,则不存在这个问题
df_mergeA.to_excel('df_mergeA.xlsx',encoding='utf_8_sig',index=False)
del df_mergeA
df_mergeA=pd.read_excel("df_mergeA.xlsx","Sheet1")
#步骤3:理论上,运行此代码即可得到填补完的合并数据集【df_mergeA_dealmissing】
df_mergeA_dealmissing=df_mergeA.copy()
for i in range(1,12):
df_val=df_mergeA.iloc[:,[0,i,i+11,i+22,i+33]]
df_val_dealmissing=cov_nan(df_val,W)
df_mergeA_dealmissing.iloc[:,[i,i+11,i+22,i+33]]=df_val_dealmissing.iloc[:,[1,2,3,4]]
"""
理论上,运行上述代码即可得到填补完的合并数据集df_mergeA_dealmissing
但实践中发现,上述代码加上函数cov_nan()内部代码,嵌套的for循环使得运行速度非常很慢
由于仅有11个变量,所以实际运行中尝试了拿掉了步骤3的for循环,改“人工手动循环” ╮(╯_╰)╭
如果有更好的编码方式,欢迎交流 (*^▽^*)~~~
""" 最后,就是将处理完的【df_mergeA_dealmissing】合并数据集恢复原来的监测点A、A1、A2、A3实测时数据的样子。
#步骤4:还原数据集,得到【df2A_new】,【df2A1_new】,【df2A2_new】,【df2A3_new】
#从处理好的【df_mergeA_dealmissing】中拆分出来
df2A_new = df_mergeA_dealmissing.iloc[:,0:12]
df2A1_new = df_mergeA_dealmissing.iloc[:,[0,12,13,14,15,16,17,18,19,20,21,22]]
df2A2_new = df_mergeA_dealmissing.iloc[:,[0,23,24,25,26,27,28,29,30,31,32,33]]
df2A3_new = df_mergeA_dealmissing.iloc[:,[0,34,35,36,37,38,39,40,41,42,43,44]]
#恢复变量名字
df2A_new.columns = list(df2A.columns)
df2A1_new.columns = list(df2A.columns)
df2A2_new.columns = list(df2A.columns)
df2A3_new.columns = list(df2A.columns)
#恢复“地点”列
s=np.repeat('监测点A', df2A_new.shape[0])
df2A_new.insert(1, '地点', s)
s=np.repeat('监测点A1', df2A1_new.shape[0])
df2A1_new.insert(1, '地点', s)
s=np.repeat('监测点A2', df2A2_new.shape[0])
df2A2_new.insert(1, '地点', s)
s=np.repeat('监测点A3', df2A3_new.shape[0])
df2A3_new.insert(1, '地点', s)2.2 缺失值处理2:随机森林插补
利用反向距离权重插值完后,对于四个监测点都是缺失值或者四个监测点中有三个缺失的,暂时还未处理,此处采用随机森林进行插值。??随机森林差值的详细介绍可查看下面文章,代码逐行讲解,十分详尽。(机器学习)随机森林填补缺失值的思路和代码逐行详解_m0_46177963的博客-CSDN博客
由于这里监测点A、A1、A2、A3有协同作用,理论上可以用以下两种方式插值,可根据意向自由选择。
方法一:用拆分数据集插值。监测点A、A1、A2、A3的实测时数据分别插值。需进行4次插值,每次处理11个变量。
方法二:用合并数据集插值。用监测点A、A1、A2、A3实测时数据的合并数据插值。只需进行1次插值,一次处理44个变量。
此处选用方法一,引用了上面博客中的代码,部分地方根据本例数据集的特征做了微调,针对监测点A“实测时数据”完整代码如下,最终得到的【df2A_dealmissing】数据集即为经协同处理和随机森林差值的不含缺失值的数据集。监测点A1、A2、A3同理。
##df2A数据预处理,续【df2A_new】
#1、一些数据准备工作
#复制一份df2A_new,插值完的数据填在df2A_dealmissing
df2A_dealmissing = df2A_new.copy()
#检验缺失值情况
df2A_dealmissing.isnull().sum(axis=0)
#2、用随机森林进行缺失值插补
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor
from sklearn.impute import SimpleImputer
#数据集中缺失值从少到多进行排序
sortindex = np.argsort(df2A_dealmissing.isnull().sum(axis=0)).values
print(sortindex)
[ 0 1 2 3 5 6 7 4 8 9 11 12 10]
#从有缺失值的列开始循环就好(结合上述分析,从sortindex[2]列开始有缺失值)
for i in sortindex[2:len(sortindex)] :
#构建新特征矩阵和新标签
df = df2A_dealmissing.copy()
fillc = df.iloc[: , i]
df.drop(df.columns[[i]],axis=1,inplace=True) #更新df,只储存用来拟合的变量
#在新特征矩阵中,对含有缺失值的列,进行0的填补,注意只能对数值部分进行填补
df_0 = SimpleImputer(missing_values=np.nan , strategy="constant" , fill_value=0).fit_transform(df.iloc[:,2:12])
#构建新的训练集和测试集
y_train = fillc[fillc.notnull()]
y_test = fillc[fillc.isnull()]
x_train = df_0[y_train.index , :]
x_test = df_0[y_test.index , : ]
#用随机森林得到缺失值
rfc = RandomForestRegressor()
rfc.fit(x_train , y_train)
y_predict = rfc.predict(x_test) #用predict接口将x_test导入,得到我们的预测结果,此结果就是要用来填补空值的
#将缺失值填补到原数据表格
df2A_dealmissing.loc[df2A_dealmissing.iloc[:,i].isnull() , df2A_dealmissing.columns[i]] = y_predict
#检验缺失值情况
df2A_dealmissing.isnull().sum(axis=0)
#删去中间产生的‘index’列
df2A_dealmissing.drop(['index'],axis=1,inplace=True)
#最终得到的df2A_dealmissing即为经协同处理和随机森林差值的不含缺失值的数据集2.3 异常值处理1:3西格玛原则
实测数据在某个小时的数值可能存在偏离数据正常分布:使用 3原则识别落在均值三倍标准差之外的异常数据。则将超过
的数据替换为
,将小于
的值替换为
。代码如下。
#续上,经缺失值处理的数据为df2A_dealmissing,将经过异常值处理的数据储存在df2A_dealoutliers中
df2A_dealoutliers=df2A_dealmissing.copy()
#计算3西格玛原则的上下界
high = df2A_dealoutliers.mean()+3*df2A_dealoutliers.std();high
low = df2A_dealoutliers.mean()-3*df2A_dealoutliers.std();low
#替换超过上下界的数值
for i in range(2,13):
i2=i-2
false_high=np.where(df2A_dealoutliers.iloc[:,i]>high[i2])[0] #找出每一列超过上界的数的位置
df2A_dealoutliers.iloc[false_high,i]=high[i2]
false_low=np.where(df2A_dealoutliers.iloc[:,i]<low[i2])[0] #找出每一列超过下界的数的位置
df2A_dealoutliers.iloc[false_low,i]=low[i2]
2.4 异常值处理2:非负数据变成0
考虑数据实际含义,浓度数据不可能为负数,因此将浓度为负的数据替换成0。代码如下
#将浓度小于零的数据替换成0,续上一步处理的df2A_dealoutliers
for i in range(2,8):
index_low_zero=df2A_dealoutliers[df2A_dealoutliers.iloc[:,i]<0].index #每一列小于0的数的索引
df2A_dealoutliers.loc[index_low_zero,df2A_dealoutliers.columns[i]]=0
#df2A_dealoutliers即为经过缺失值(协同处理+随机森林)和异常值处理(3西格玛+非负数)的sheet2数据
#为方便后续阅读,将预处理完的df2A数据储存为dfA_real_hour,意为监测点A实测时数据
dfA_real_hour = df2A_dealoutliers.copy()到此为止,附件1sheet2“监测点A逐小时污染物浓度与气象实测数据”预处理工作已全部完毕,此处将最终预处理完的df2A数据储存为【dfA_real_hour】,意为监测点A实测时数据。监测点A1、A2、A3经反向距离权重插值后,处理方式与监测点A一致。
Attention:这里的【dfA_real_hour】与博主另一篇文章《[Python]数据预处理例题:2021华为杯数学建模B题“空气质量预报二次建模”》2.2.5节产生的【dfA_real_hour】无论是数据条数还是插值结果都不是完全一样的。因为在缺失值处理部分,这里用了A、A1、A2、A3四个监测点的数据进行插值,而那篇博客中不考虑监测点间的协同作用,只用了自己本身的“删失处理”+“随机森林插值”。