[人工智能]论文笔记-DynaSLAM II: Tightly-Coupled Multi-Object Tracking and SLAM

I.Introduction

关于动态SLAM，在这个部分，论文总结了现有三种方案思路：

1. 检测动态的区域，然后把他们从SLAM环节中去除
2. 在定位的环节外，把包含动态内容的现实图片中翻译成只有静态内容的图片
3. 一个小的却在发展的思路：把动态物体也放进问题里，不仅要去解决SLAM的问题，还要为动态物体的位姿提供信息。

对于第三种思路，论文中也给出了几个解决思路：

1. 使用传统的多目标追踪。缺点是：准确度高度依赖于相机的位姿估计，但在复杂的动态环境下，位姿肯定是不准的（鸡生蛋蛋生鸡问题）
2. 近几年，大家开始尝试联合视觉SLAM同时解决动态物体追踪的问题（把问题搞得更复杂了233）这些系统通常是为特殊的使用情况而定制的，并利用多种先验因素来约束空间解决方案。比如：道路平面结构和驾驶场景中的平面物体运动，甚至使用物体的三维模型。

DynaSLAM II 概述
这是一个开源的对于动态环境的双目/RGBD SLAM系统，它可以同时估计i相机的位姿，地图以及运动物体的轨迹。论文提出了一个使用BA的解决方案，在局部时间窗口中严格优化场景结构、相机姿势和物体轨迹。物体的Bounding Box也在一个解耦的公式中被优化，这个公式可以估计物体的尺寸和6个DoF的位姿，而不针对任何特定的使用情况。

III.Method

这个系统是基于ORB-SLAM2的。输入是经过时间同步的双目或者RGBD图片，输出是每一帧相机和动态物体的位姿，以及一个包括动态物体的空间/时间地图，使用到了语义和实例信息作为先验。整体思路如下：

1. 对于每一帧，都会对它进行像素级别的分割，这一帧图像的ORB特征的提取和匹配通过双目图像对(stereo image pairs)完成。
2. 将当前帧的静态和动态特征与前一帧&地图里的两类特征关联起来，这里假设摄像机和被观测物体都是匀速运动。
3. 然后根据动态特征的对应关系来匹配物体实例。静态匹配被用来估计摄像机的初始姿态，动态匹配则用来计算移动物体的SE(3)变换。
4. 最后，相机和物体的轨迹，以及物体的bounding box和三维点通过有边缘化的滑动窗口和一个soft smooth motion prior进行优化.

A.Notation

对于双目或者RGB-D相机i，它在世界坐标系$W$下第i时刻的位姿为 $T_{CW}^i\in SE(3)$，从相机i可以观察到：
1）静态3D地图点，$x_W^l\in {\mathbb{R}}^3$
2）动态物体k在世界坐标系下的位姿$T_{WO}^{k,i}\in SE(3)$,它在时刻$i$的线速度和角速度$v_i^k,w_i^k\in {\mathbb{R}}^3$, 注意这些都是在物体坐标系下的(Object)。而动态物体k上的动态点表示为$x_O^{j,k}\in {\mathbb{R}}^3$

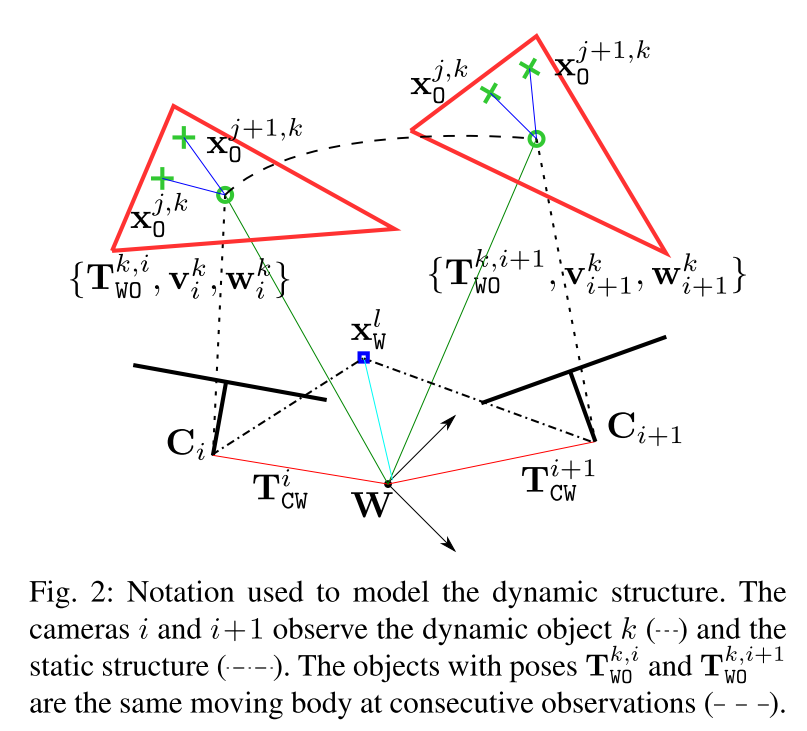
从这幅图里，可以看到世界坐标系在W，$C_i$和$C_{i+1}$是相机前后帧的位置，蓝点为环境中静止的点，红色三角形是在移动的物体，绿色小圆是这个移动物体的重心位置，绿色十字是在这个移动物体上提取出的特征点。

B. Objects Data Association

数据关联的流程大概是这样的：

1. 先对输入的每一帧新数据进行像素级的语义分割和ORB特征的提取与匹配。
2. 对于分割后的结果来说，根据语义信息，就会有动态和静态之分。首先，先对静态特征进行数据关联，先把当前帧的静态特征跟上一帧以及map中的静态特征进行匹配?。
3. 接下来再看动态特征。对于动态特征，这里就引入了一个概念：Object（这里个人的理解是，因为后续需要对动态点进行追踪，会把落在同一个物体上的动态点都看成一个object，相当于对一个动态物体进行追踪）。那么，满足什么条件才能创建一个Object呢？如果一个instance属于动态类别（比如汽车，行人，动物），同时这个instance包括了大量新的附近的关键点，此时就会创建一个新的Object（属于动态类别而且关键点要足够多）。有了这个Object之后，和他对应的关键点就会被分配到这个Object中。
4. 接下来，会用两种方式把当前帧的动态特征点和local map的动态点相关联： a) 如果map objects的速度已知，就在匀速运动假设的基础上构建重投影来找到匹配关系; b) 如果map objects的速度没有初始化，或者用a)方法没有找到足够数量的匹配关系，就在前后帧暴力匹配那些有最大重叠面积的实例上的特征点。注意：这个工作可以解决遮挡问题，因为当前帧的动态关键点是和map objects匹配的，而不是和上一帧中的objects。
5. 上面的方法是进行了动态点之间的数据关联，除此之外，还需要更高级的在instances和objects之间的关联(也就是在物体级别的关联)。如果当前帧一个新object上的大部分关键点都和一个map object上的点匹配上了，那这两个objects就会有相同的track id。为了让这个高层级的数据关联更加鲁棒，还会在IoU的基础上进行parallel instance-to-instance的匹配，这个IoU是根据CNN instances 2D bounding boxes计算出来的（多物体追踪常用这种方式）。

接下来展开来讲一下第五点。追踪的第一个object的位姿($SE(3)$)是用这些3D点的质心和单位阵来初始化的。为了预测这个Track中物体后续的位姿，使用了匀速运动模型以及通过最小化重投影误差来精细化object的位姿估计。

多视角几何问题中常用的重投影误差定义如下：

对于一个相机i，它的位姿是$T_{CW}^i\in SE(3)$, 一个3D地图点l在参考系$W$的齐次坐标为${\overline{x}}_w^l\in {\mathbb{R}}^4$，它的双目匹配关键点的坐标是$u_i^l=[u,v,u_R]\in {\mathbb{R}}^3$(观测值), 那么这个相机的重投影误差就是
$$e_{repr}^{i,l}=u_i^l?{\pi }_i(T_{CW}^i?{\overline{x}}_W^l)(1)$$
在这个式子中，${\pi }_i$是一个校正过的双目相机或者RGBD相机的重投影函数。这个函数可以把相机坐标系中的一个3D齐次点投影到相机的像素上。不过上面的这个式子是针对静态情况的，下面的公式用于动态的情况：
$$e_{repr}^{i,j,k}=u_i^j?{\pi }_i(T_{CW}^i?T_{WO}^{k,i}?{\overline{x}}_O^{j,k})(2)$$
这个式子中，$T_{WO}^{k,i}\in SE(3)$是相机$i$观察到的，在世界坐标系下物体k的位姿的逆。${\overline{x}}_O^{j,k}\in {\mathbb{R}}^4$是动态点$j$在对应的移动物体参考k下的3D齐次坐标，此时相机$i$的观测是$u_i^j\in {\mathbb{R}}^3$. 这个式子可以联合优化相机和动态物体的位姿，还可以优化3D点的位置。(一点小理解：就是增加了物体坐标系这个媒介，把物体坐标系下某一点的坐标转到世界坐标系再转到相机坐标系再到像素坐标)

C.Object-Centric Representation

为什么要用这种表示方法？
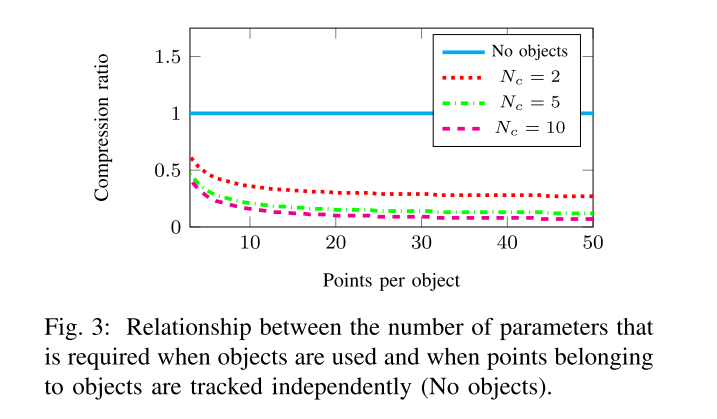
考虑到相比于单纯的SLAM问题，跟踪移动物体还会带来额外的复杂性，额外的参数数量，所以要尽可能地减少参数数量以保持实时性能。
在通常的动态SLAM工作中，通过形成独立的点云将动态点建模为重复的三维点？？，会导致参数数量过大。比如说，给了$N_C$个相机，所有相机可以观察到 $N_O$个动态物体，每个动态物体上有$N_{OP}$个3D点，那么，用于追踪动态物体的参数个数就是：$N=6N_C+N_C?N_O?3N_{OP}$. 如果是静态SLAM的话，参数个数就是$N=6N_C+N_O?3N_{OP}$（可以结合上面的Fig2思考）。
具体怎么解决？
引入Object的概念，这个问题就可以改善很多。因为物体上的3D点都是独一无二的，这些点可以被它所在的动态物体作为参考？？，随着时间的变化，被建模的就是objects的位姿，这是参数个数就变成了$N^{\prime }=6N_C+N_C?6N_O+N_O?3N_{OP}$. 下图表示了对于10个物体的参数压缩率，即$N^{\prime }/N$. 这种对动态物体和动态点的建模方式节省了大量参数。

D. Bundle Adjustment with Objects Bundle

在得到了匹配点对和好的初始位姿估计之后，BA可以用来为相机位姿提供更加准确的估计，还可以进行稀疏的几何重建。这里论文作者假设，如果把object的位姿联合优化，进行BA也可能有类似的效果。
静态：
通过最小化到匹配的关键点$u_i^l$的重投影误差来优化静态地图3D点${\overline{x}}_W^l$和相机位姿$T_{CW}^i$， 使用的是上面的公式(1)。
动态：
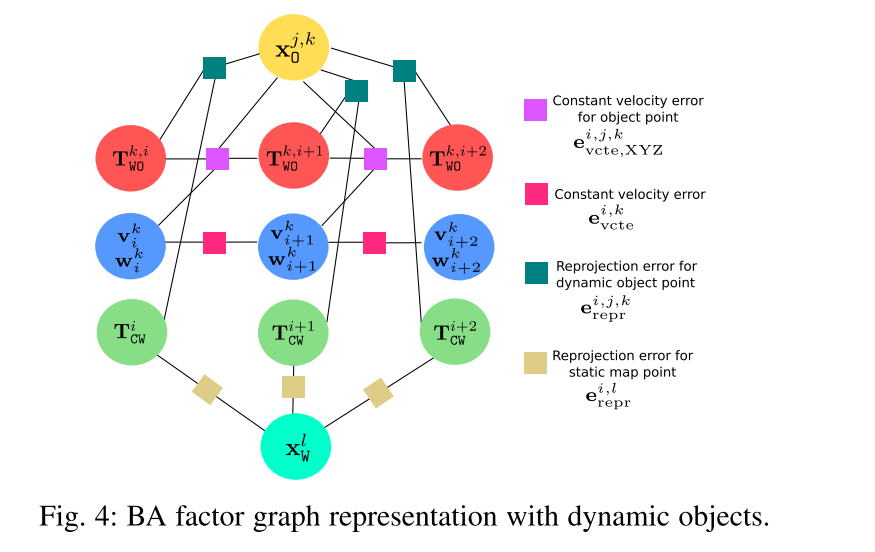
移动物体上的点${\overline{x}}_O^{j,k}$, 相机位姿$T_{CW}^i$,物体的位姿$T_{WO}^{k,i}$可以通过最小化(2)的重投影误差来细化，BA因子图如下所示：
插入一个关键帧到地图的两个条件：

1. 相机的tracking很弱（原因和ORB-SLAM2中一样）
2. 对于任意场景object的追踪都很弱。比如说，一个有大量特征点的object只在当前帧追踪到了很少的点，这种情况下，关键帧会被插入地图，会创建一个新object，和新的object points。

Tracking时使用局部BA的几种情况：

• 如果相机的tracking不弱，这个关键帧就不会引入新的静态地图点；如果剩下的动态物体有稳定的tracking，那么对这些tracks就不会创建新的objects。
• 对于优化来说，如果只是因为相机tracking很弱就插入一个关键帧，那么就和ORB-SLAM2中一样，用局部BA优化当前处理的关键帧，所有和当前关键帧在共视图里相联系的关键帧，以及所有能被这些关键帧看到的地图点都同理。
• 对于动态数据，如果一个关键帧被插入只是因为对一个object的tracking很弱，那么就用局部BA沿着2秒的时间尾巴along a temporal tail of 2 seconds?? 优化该物体和相机的位姿和速度。
• 如果一个关键帧被插入是因为对相机和objects的tracking都很弱，那么相机位姿，地图结构，object的位姿&速度&点都会被联合优化

为了避免出现物理上不可行的物体动态，通过在连续观测中用匀速假设来强迫有一个平滑的轨迹。对于相机$i$，物体k的线速度和角速度分别为$v_i^k\in {\mathbb{R}}^3$和$w_i^k\in {\mathbb{R}}^3$。定义如下误差项：
$$e_{vcte}^{i,k}=\left(\begin{array}{c}{v}_{i+1}^k?v_i^k\\ w_{i+1}^k?w_i^k\end{array}\right)(3)$$
还需要一个额外的误差项来耦合物体的速度与物体位姿及其相应的三维点：
$$e_{vcte,XYZ}^{i,j,k}=(T_{WO}^{k,i+1}?T_{WO}^{k,i}\Delta T_{O_k}^{i,i+1}){\overline{x}}_O^{j,k}(4)$$
其中的$\Delta T_{O_k}^{i,i+1}$满足下面的定义, $Exp:{\mathbb{R}}^3\to SO(3)$ ：
$$\Delta T_{O_k}^{i,i+1}=\left(\begin{array}{cc}Exp(w_i^k\Delta t_{i,i+1})& v_i^k\Delta t_{i,i+1}\\ 0_{1\times 3}& 1\end{array}\right)(5)$$

所以最后BA问题就变成了：
对可优化的局部窗口$C$中的一组相机的BA问题，每个相机$i$观察到一组地图点$M{P}_i$和一个物体集合$O_i$,这个集合包含每个物体k上的object points $O{P}_k$（可以对照上面的因子图比对！）。
$$\begin{gathered} \underset{\theta }{\min }\sum _{i\in C}(\sum _{l\in M{P}_i}\rho (||e_{repr}^{i,l}|{|}_{{\sum }_i^l}^2)+\sum _{k\in O_i}(\rho (||e_{vcte}^{i,k}|{|}_{{\sum }_{\Delta t}}^2) \\ +\sum _{j\in O{P}_k}(\rho (||e_{repr}^{i,j,k}|{|}_{{\sum }_i^j}^2)+\rho (||e_{vcte,XYZ}^{i,j,k}|{|}_{{\sum }_{\Delta t}}^2)))) \end{gathered}$$
待优化变量为：
θ = { T C W i , T W O k , i , X W l , X O j , k , v i k , w i k } \theta = \{T_{CW}^i, T_{WO}^{k,i}, X_W^l, X_O^{j,k}, v_i^k, w_i^k\} θ={TCWi?,TWOk,i?,XWl?,XOj,k?,vik?,wik?}
公式中的$\rho$是huber cost function,用来减轻外点的权重； $\sum$是协方差矩阵。可以看到最后的公式中有两个重投影误差的项，两个其他的误差项：

• 对于重投影误差项，Σ与分别观测点l和j点的相机$i$中的关键点的尺度有关。
• 对于其他两个误差项，Σ与一个物体的两个连续观测值之间的时间间隔有关，即时间越长，恒速假设的不确定性越大。

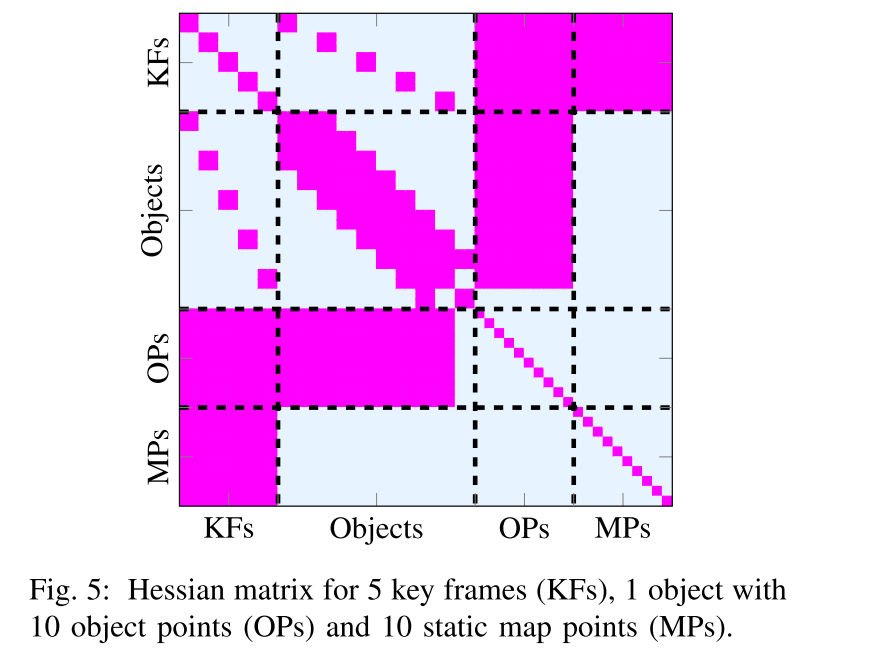
下面的图例画出了这个问题的hessian矩阵，Hessian可以通过因子图中每条边的雅格比矩阵得出。为了有一个非零的（i，j）块矩阵，在因子图中i和j节点之间必须有一条边？？？。注意：地图点和物体点的稀疏性模式的不同。Hessian矩阵的大小由地图点数量$N_{mp}$和物体上的点的数量决定(比相机和物体的数量大几个数量级)。使用舒尔补让该系统的运行时间复杂性为$O(N_c^3+N_c^2{N}_{mp}+N_c{N}_o{N}_{op})$，其中第二项或第三项将占主导地位,这取决于由静态点数量、动态点数量导致的计算成本。

E. Bounding Boxes

这一个点是物体三维点第一次被观测时的质量中心。尽管随着时间的推移，质心会随着新点的观测而改变，但被跟踪和优化的物体姿态是指这个第一质心（如何保证？？）。为了充分了解移动的周围环境，了解物体的尺寸和空间占有率是非常重要的。

数据关联和BA步骤的输出包括：相机位姿，静态场景和动态物体的结构，每个object上某一点的6DoF的轨迹；这个某一点是特指这个物体的3D点第一次被观察到时的质心的位置。尽管质心会随着新的点观察而改变，但是可以通过track和优化得到的物体位姿来算出第一个质心的位置。

为了进一步理解周围的移动物体，还需要知道物体的维度和空间占用。

把物体轨迹估计和物体的bounding box估计解耦的好处？
允许从动态物体出现的第一帧开始追踪它们，不受摄像机–物体视点的影响。
具体步骤

• 通过搜索两个大致适合物体上大多数点的垂直平面来初始化一个物体的bounding box。我们假设，即使物体并不总是完美的立方体，但许多物体可以大致找到合适的3D bounding box。
• 如果对某些物体只找到一个平面怎么办？
  在不可观方向的粗略尺寸？？上增加一个与物体类别有关的先验。这个过程是在RANSAC中完成的：我们选择计算出一个三维bounding box，它在图像的投影与CNN的二维b-box有最大的IoU。这个bounding box对每个object track都要计算一次。

目的：为了求到更精确的bounding box的尺寸和它相对于物体追踪参考的位姿, 需要：
1） 使用在一个时间窗口内的基于图像的优化。这种优化旨在使三维bounding box在图像上的投影和CNN二维bounding box预测值之间的距离最小。鉴于这个问题对于一个少于三个视图的物体来说是不可观的，因此只有在一个物体至少有三个观察的关键帧时才会执行。
2）为了约束解空间，以防物体的视角使这个问题不可观察（例如，从后面观察的汽车），所以还会使用一个关于物体尺寸的软先验。由于这个先验与物体类别密切相关，我们认为加入这个软先验并不意味着丧失通用性。所以最终，初始bounding box的位姿被设定为一个先验，以便优化方案保持接近？？。

IV. EXPERIMENTS

这一节主要就两个方面对系统进行了测试，一个是评估tracking objects对于相机运动估计的影响；一个是分析多物体跟踪的表现。

A. 视觉里程计

a. 和自家实验室成果的比较

使用了Kitti的tracking和raw数据集，并且是对ORB-SLAM2，DynaSLAM以及DynaSLAM II进行了比较。这三个工作都是这个实验室做的，相当于有一个层层递进的关系，ORB-SLAM2是所有的baseline，DynaSLAM在这个基础上加了检测属于动态物体上的特征的功能，但没有在后续使用这些特征，而DynaSLAM II就是对这些动态物体的特征进行了更多的处理。
对于前两个系统，他们表现的区别，就是在于场景中的移动物体到底有多“动态”，如果移动的物体具有代表性而且处于运动状态，DynaSLAM的结果就会更好；但如果物体具有代表性但处于静止状态（比如静止的车），DynaSLAM就会有很大的轨迹误差，因为属于静态车辆上的特征（往往会在相邻帧中出现）没有被用到位姿估计中去。而DynaSLAM II在这两种情况下表现都还挺不错，原因有两个方面：
1）现实场景中，经常会有动态物体遮挡住静态场景的情况，导致静态特征只能给相机的旋转估计提供帮助，而DynaSLAM II中估计出了动态物体的速度，就可以给BA提供更多的信息（尤其是在静态特征不足时）。
2）当属于动态类的物体实际是静止时，DynaSLAM II也会对他上面的特征点进行跟踪，得到的速度是趋近于0的，所以这个物体上的点实际也会类似于静态点。

b. 和其他同类型系统的比较

这里主要和ClusterVO和VDO-SLAM进行了比较，前者可以用于双目和RGB-D数据，后者只能用RGB-D数据。
论文的方法可以实现一个较低的平移相对误差，而VDO-SLAM是能得到较低的旋转相对误差，原因在于：
远点可以更好的进行旋转估计，作者认为这是由于相机位姿估计算法和传感器的不同导致的，不是因为加入了动态物体跟踪导致DynaSLAM II在这方面表现稍弱一点。

B. 多物体跟踪

使用kitti的tracking数据集，lidar点云数据中有人工标记的动态物体的轨迹和3D bounding box。
关于这一项的指标，论文作者使用了一下两个：
1）CLEAR MOT metric MOTP，论文中的方法可以减小截断和遮挡在精度上造成的影响，但是只能找到更少的bounding box。 2D MOTP其overlapping指的是3D bounding boxs投影到当前帧的IoU； BV MOTP指的是bounding box在鸟瞰图下的IoU的overlapping；3D MOTP指的是对应的在3D情况下的。
2）被追踪的物体的轨迹质量，比较ATE和RPE。关于这里，作者提到，汽车的轨迹误差是acceptable但是比其对相机位姿估计的表现差了很多，他们感觉是因为基于特征的算法使用在bounding box估计上是非常有挑战的，如果是大量的（感觉是想说稠密的点）3D点，就可以为object tracking提供更多的信息。

对于本论文的方法，如果物体离相机太远，可能就会导致检测丢失，双目匹配也不能提供足够的特征进行rich tracking；此外，对行人的tracking比对汽车的准确度要低，因为行人属于非刚体。

C. 时间分析

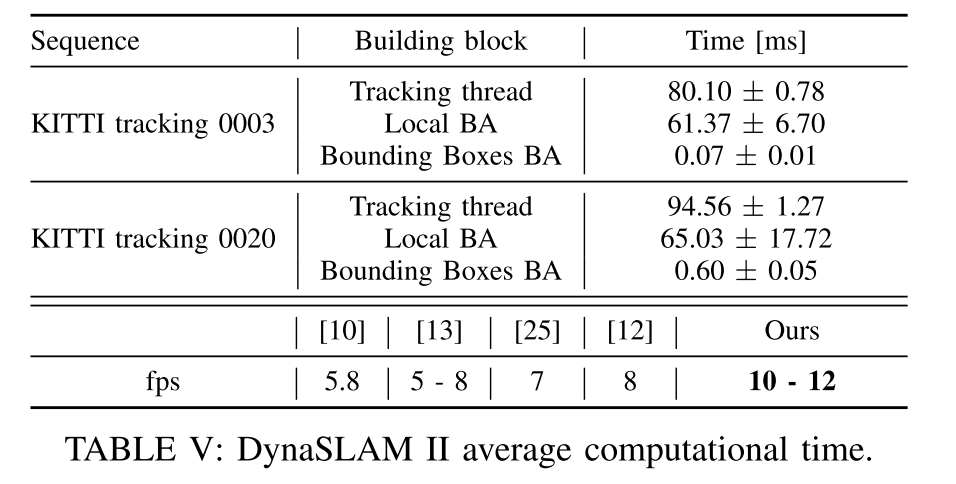
DynaSLAM II的用时和跟踪物体的数量高度相关。如果只有不超过2个物体，KITTI tracking 0003的帧率是12fps，0020序列最多有20个物体，性能略微有些影响，帧率大概在10fps。这里没有算入进行语义分割的时间。DynaSLAM II目前是唯一能满足SLAM和多物体跟踪的实时方案。

V.CONCLUSIONS AND FUTURE WORK

这一节中作者提到了算法的局限性，由于算法的核心是基于特征点，所以在找到准确的3D bounding box和追踪低纹理物体时会有局限；如果能够完全使用稠密的视觉信息一定能推进这个极限。他们后续可能会尝试单目情况下的加入了多物体追踪的系统，动态物体追踪其实可以为地图的尺度提供丰富的信息。

一点读后感：真的是神仙实验室啊！如果发现整理的笔记哪里有问题/错误的话，欢迎留言讨论！然后也有一些没有完全理解的地方，如果能有人一起讨论就更好了~