一个简单的神经网络示意图

1.神经网络
(1)定义:神经网络是由神经元按层次结构组成的网络状图形单元
- 输入层:包含输入神经元
- 输出层:包含输出神经元
- 隐藏层:既不包含输入神经元也不包含输出神经元
(2)前馈神经网络:以上一层的输出作为下一层的输入,神经网络中不存在回路
2.激活函数
(1)为什么需要激活函数
-
不添加激活函数时的多层神经网络系统实际上可以等效为一个仅有输入输出层的神经网络。
α 2 = α 1 ω 1 + b 2 α 3 = α 2 ω 2 + b 3 = ( α 1 ω 1 + b 2 ) ω 2 + b 3 = α 1 ( ω 1 ω 2 ) + ( b 2 ω 2 + b 3 ) . . . \alpha^2=\alpha^1\omega^1+b^2 \\ \alpha^3=\alpha^2\omega^2+b^3 \\ =(\alpha^1\omega^1+b^2)\omega^2+b^3 \\ =\alpha^1(\omega^1\omega^2)+(b^2\omega^2+b^3) \\ ... α2=α1ω1+b2α3=α2ω2+b3=(α1ω1+b2)ω2+b3=α1(ω1ω2)+(b2ω2+b3)...
类似的可以推出每增加一层都可以用新的等效式表示为一个仅有输入输出层的神经网络。由此,激活函数首先要能够改变变量间原有的线性关系。然后,把神经网络理解为对输入向量中每个量的权重进行各种组合调整,最后训练到能满足预测需求的模型。每一层的 z z z的值表示了对应特征量权重组合的权重,而激活函数对 z z z的权重进行重新评估,在靠近边界时变化迅速在远离边界时变化平缓。
(2)常用的激活函数
- sigmoid函数: y = 1 1 + e ? x y=\frac{1}{1+e^{-x}} y=1+e?x1?

-
tanh函数: y = e x ? e ? x e x + e ? x y=\frac{e^x-e^{-x}}{e^x+e^{-x}} y=ex+e?xex?e?x?

-
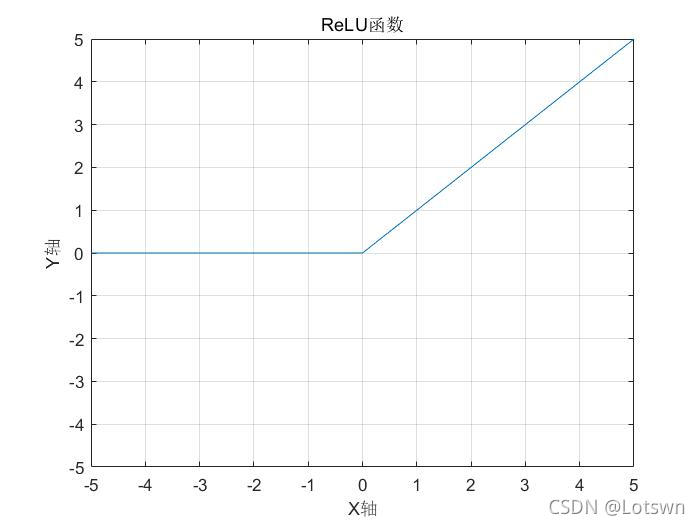
ReLU函数: y = m a x ( 0 , x ) y=max(0,x) y=max(0,x)
3.代价函数
(1)二次代价函数
-
C = 1 2 m ∑ m ∣ y ? a ∣ 2 C=\frac{1}{2m}\sum_m|y-a|^{2} C=2m1?∑m?∣y?a∣2
-
学习缓慢问题
? C ? ω = ( a ? y ) σ ′ ( z ) x ? C ? b = ( a ? y ) σ ′ ( z ) \frac{\partial C}{\partial \omega} =(a-y)\sigma'(z)x \\ \frac{\partial C}{\partial b} =(a-y)\sigma'(z) ?ω?C?=(a?y)σ′(z)x?b?C?=(a?y)σ′(z) -
易得上式,当出现z趋近1或0的情况时时,sigmoid的导数趋近0。
-
故代价函数关于权重和偏置的偏导数也将趋近0,此时如果继续进行训练修改参数,代价函数变化缓慢,模型不会的效果不会有明显提升。
(2)交叉熵
-
C = ? 1 m ∑ m { y ln ? a + ( 1 ? y ) ln ? ( 1 ? a ) } C = - \frac{1}{m} \sum_m\{y \ln a +(1-y) \ln (1-a) \} C=?m1?∑m?{ylna+(1?y)ln(1?a)}
-
ρ C ρ ω = 1 m ∑ x x ( σ ( z ) ? y ) ρ C ρ β = 1 m ∑ x ( σ ( z ) ? y ) \frac{\rho C}{\rho\omega} = \frac{1}{m} \sum_x x(\sigma(z)-y) \\\frac{\rho C}{\rho\beta} = \frac{1}{m} \sum_x (\sigma(z)-y) ρωρC?=m1?x∑?x(σ(z)?y)ρβρC?=m1?x∑?(σ(z)?y)
此时代价函数的偏导数随预测值偏差得到增大而增大,此时模型具有良好的自律性,并不会出现学习缓慢问题。
(3)柔性最大值(softmax)与对数似然代价
柔 性 最 大 值 激 活 函 数 ??????? α j L = e z j L ∑ k e z k L 对 数 似 然 代 价 ???? C = ? l n a y l 柔性最大值激活函数\ \ \ \ \ \ \ \alpha_j^L = \frac{e^{z_j^L}}{\sum_ke^{z_k^L}} \\ 对数似然代价\ \ \ \ C=-lna_y^l 柔性最大值激活函数???????αjL?=∑k?ezkL?ezjL??对数似然代价????C=?lnayl?
-
柔性最大值描述了第j个输出在当前层输出之和中的占比
-
柔性最大值不会出现学习缓慢的情况
-
反向传播(这里我不确定)
δ j l = ? C ? a j l σ ′ ( z j l ) = a j l ? y i \delta^l_j=\frac{\partial C}{\partial a^l_j} \sigma'(z^l_j)=a^l_j-y_i δjl?=?ajl??C?σ′(zjl?)=ajl??yi?
4.调整权重与阈值
神经网络的输出由输入x与权重 ω \omega ω和偏置b决定,找到合适的 ω \omega ω和b便是我们训练神经网络的目的。根据代价函数的结果评价 ω \omega ω和b的价值。
(1)梯度下降算法
当输入相同,改变
ω
\omega
ω和b即将代价函数视作关于变量
ω
\omega
ω和b的函数,可得:
Δ
C
≈
?
C
?
ω
Δ
ω
+
?
C
?
b
Δ
b
\Delta C \approx \frac{\partial C}{\partial\omega}\Delta\omega+\frac{\partial C}{\partial b} \Delta b
ΔC≈?ω?C?Δω+?b?C?Δb
(
ω
\omega
ω和b并不代表只有一个权重和一个偏置)
令 Δ ω = ? ? C ? ω , Δ b = ? ? C ? b \Delta \omega= - \frac{\partial C}{\partial\omega},\Delta b=-\frac{\partial C}{\partial b} Δω=??ω?C?,Δb=??b?C?,易得 Δ C < 0 \Delta C < 0 ΔC<0,意味着沿着这样的变化代价函数将逐渐减小,直到 ω \omega ω和b令人满意。
这就是梯度下降算法,
η
\eta
η即梯度下降算法的学习率,用来调节梯度下降的步伐,以求更好的近似度。
ω
k
=
ω
k
?
η
?
C
?
ω
b
k
=
b
k
?
η
?
C
?
b
\omega_k= \omega_k- \eta\frac{\partial C}{\partial\omega}\\ b_k=b_k-\eta\frac{\partial C}{\partial b}
ωk?=ωk??η?ω?C?bk?=bk??η?b?C?
(2)反向传播算法
在梯度下降算法中我们知道了如何改变权重与偏置的值,但计算 ? C ? ω \frac{\partial C}{\partial\omega} ?ω?C?仍然是件麻烦的事,因此引入了反向传播算法。
- 定义 δ j l ≡ ? C ? z j l \delta^l_j \equiv \frac{\partial C}{\partial z^l_j} δjl?≡?zjl??C?,表示第l层第j个神经元上的误差,这里的误差是我们假设的,以研究其对代价函数的改变
- 反向传播的四个基本方程
- BP1: δ j l = ? C ? a j l σ ′ ( z j l ) \delta^l_j=\frac{\partial C}{\partial a^l_j} \sigma'(z^l_j) δjl?=?ajl??C?σ′(zjl?)
- BP2: δ l = ω l δ l + 1 σ ′ ( z l ) \delta^l=\omega^l\delta^{l+1}\sigma'(z^l) δl=ωlδl+1σ′(zl)
- BP3: ? C ? b l = δ l \frac{\partial C}{\partial b^l}=\delta^l ?bl?C?=δl
- BP4: ? C ? w j k l = a j l δ k l + 1 \frac{\partial C}{\partial w^l_{jk}}=a^l_j\delta^{l+1}_k ?wjkl??C?=ajl?δkl+1?
反向传播的四个方程给出了计算 ? C ? ω \frac{\partial C}{\partial\omega} ?ω?C?和 ? C ? b \frac{\partial C}{\partial b} ?b?C?的方法,也解释了为什么要反向推导。
5.规范化
(1)过拟合
神经网络在训练中越来越只能表现出training_data的特征,而不能很好的适用于test_data以及其它数据集,在经历一定epoch,test_data的准确率将维持在一个并不能令人满意的水平。
检验:使用validation_data数据集,在每个迭代期后检验分类准确率,在准确率饱和时应当停止训练,继续训练模型就会过拟合了。
(2)L2规范化
- 引入规范化项: λ 2 m ∑ ω 2 \frac{\lambda}{2m}\sum \omega^2 2mλ?∑ω2,将大的权重减小
- 规范化参数: λ > 0 \lambda > 0 λ>0
- 规范化代价函数: C = C 0 + λ 2 m ∑ ω ω 2 = ? 1 m ∑ x { y ln ? a + ( 1 ? y ) ln ? ( 1 ? a ) } + λ 2 m ∑ ω ω 2 C=C_0+\frac{\lambda}{2m}\sum_\omega \omega^2=- \frac{1}{m} \sum_x\{y \ln a +(1-y) \ln (1-a) \}+\frac{\lambda}{2m}\sum_\omega \omega^2 C=C0?+2mλ?∑ω?ω2=?m1?∑x?{ylna+(1?y)ln(1?a)}+2mλ?∑ω?ω2(以交叉熵为例)
(3)其它规范化
- L1规范化^规范项 λ n ∑ ω ∣ ω ∣ \frac{\lambda}{n}\sum_\omega |\omega| nλ?∑ω?∣ω∣ ,将大的权重在高位趋同,将小的权重在低位趋0
- 弃权:每个epoch随机删除隐藏层神经元 ω 2 \omega^2 ω2(以交叉熵为例)
(3)其它规范化
- L1规范化:规范项 λ n ∑ ω ∣ ω ∣ \frac{\lambda}{n}\sum_\omega |\omega| nλ?∑ω?∣ω∣,将大的权重在高位趋同,将小的权重在低位趋0
- 弃权:每个epoch随机删除隐藏层神经元