开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 多元线性回归算法预测房价 -> 正文阅读

[人工智能]多元线性回归算法预测房价

文章目录

一、多元线性回归理解
二、波士顿房价案例
三、数据清洗（数据预处理）
四、使用Excel实现回归
- 1.回归实现
- 2、回归分析
五、使用代码实现回归
- 使用Statsmodels建立多元线性回归模型
- 使用Sklearn库建立多元线性回归模型
六、总结
七、参考链接

一、多元线性回归理解

线性，图像上任意一点的坐标,y值都是x值的a倍.我们把这种横纵坐标始终呈固定倍数的关系叫做"线性".线性函数的图像是一条直线.所以我们知道了多元线性回归函数的图像一定也是一条直线，多元，顾名思义，就是表达式中存在多个自变量(属性)，
多元线性回归就是:用多个x(变量或属性)与结果y的关系式来描述一些散列点之间的共同特性.这些x和一个y关系的图像并不完全满足任意两点之间的关系(两点一线),但这条直线是综合所有的点,最适合描述他们共同特性的,因为他到所有点的距离之和最小也就是总体误差最小.

二、波士顿房价案例

市场房价的走向受到多种因素的影响，通过对影响市场房价的多种因素进行分析，有助于对未来房价的走势进行较为准确的评估。
??通过对某段时间某地区的已售房价数据进行线性回归分析，探索影响房价高低的主要因素，并对这些影响因素的影响程度进行分析，利用分析得到的数据，对未来房价的趋势和走向进行预测。
??本文探究街区(neighborhood)，房屋面积(area)，卧室数bedrooms，浴室数bathrooms，房屋风格(style)与房价(price)的关系已经影响大小。
在这里插入图片描述

三、数据清洗（数据预处理）

学习参考资料“多元线性回归模型预测房价.ipynb”，自己实践重新做一下针对房屋数据集“house_prices.csv”的多元线性回归（基于统计分析库statsmodels）；并重点理解
偏差数据、缺少数据的预处理（数据清洗）、“特征共线性”的检测方法以及统计学的传统估计参数。

1、数据预处理

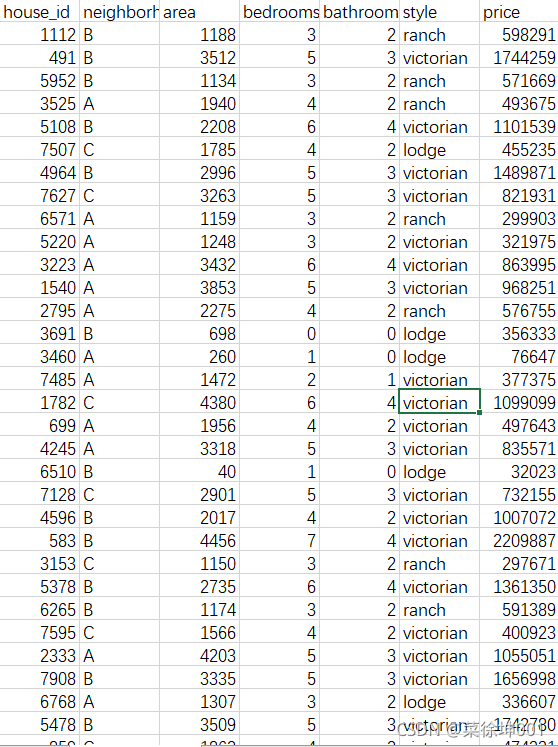
在观察原始数据的过程中我们不难发现：有些房屋面积（area）过小、没有卧室或者卫生间等疑似错误。所以，我们要先对数据进行清洗，之后才能利用。
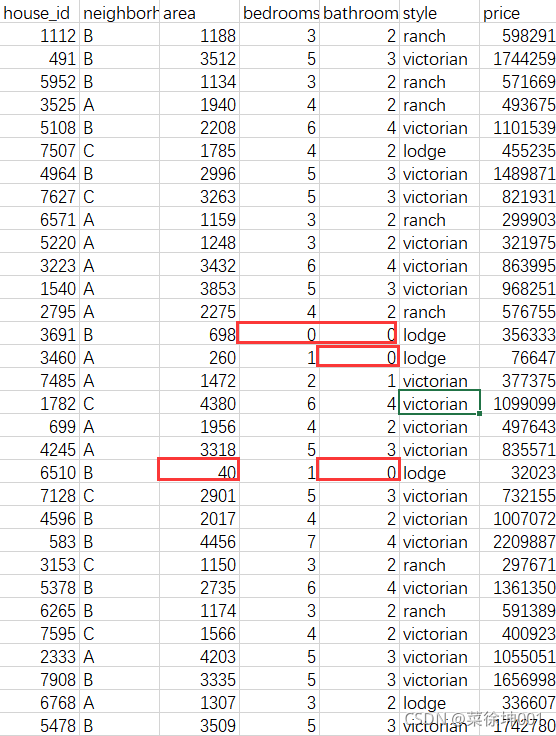
在这里插入图片描述

2、数据筛选

在这里插入图片描述
将bedroom等于0的筛选掉

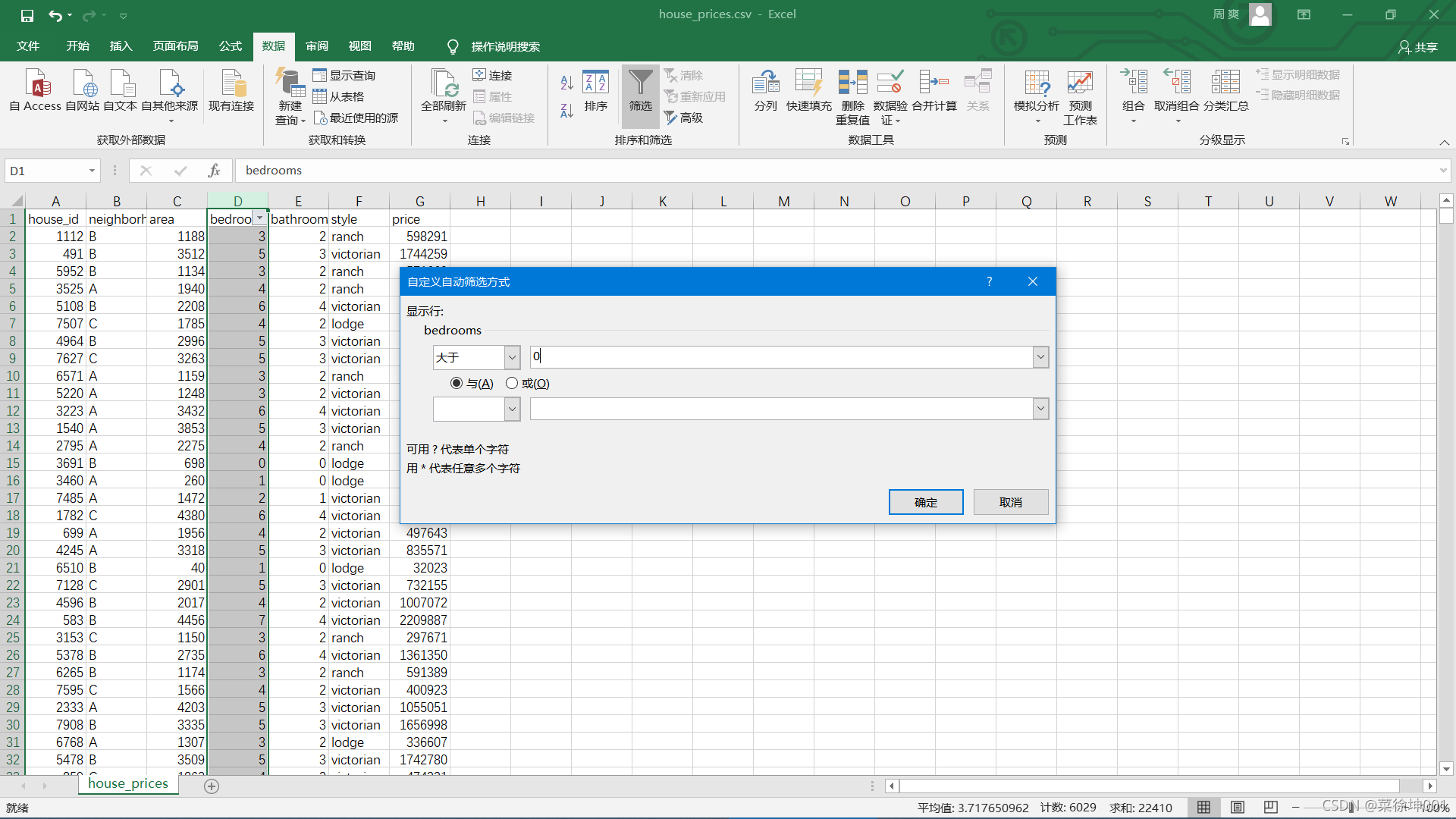
将bathroom等于0的筛选掉

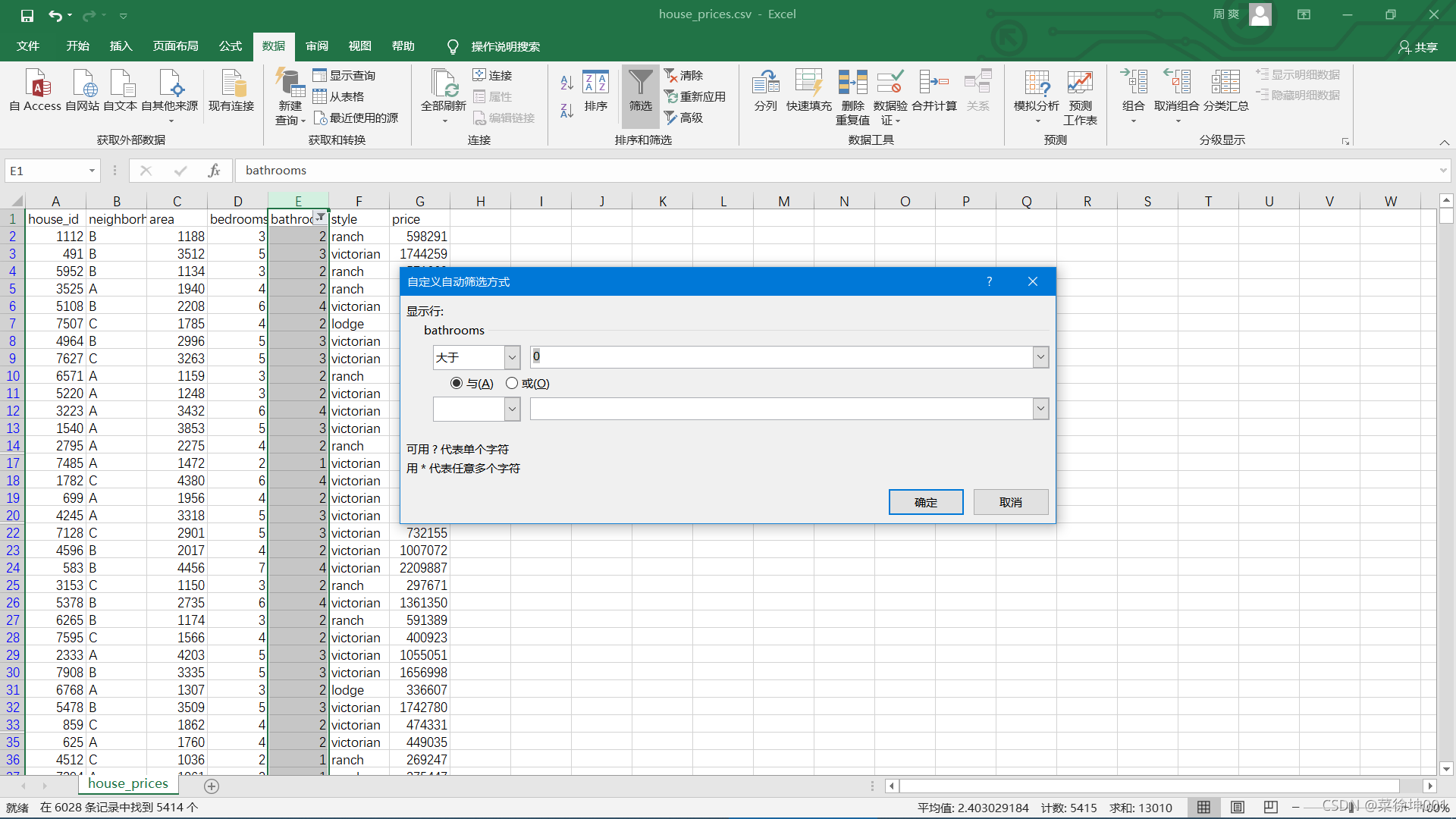
将area小于200的筛选掉

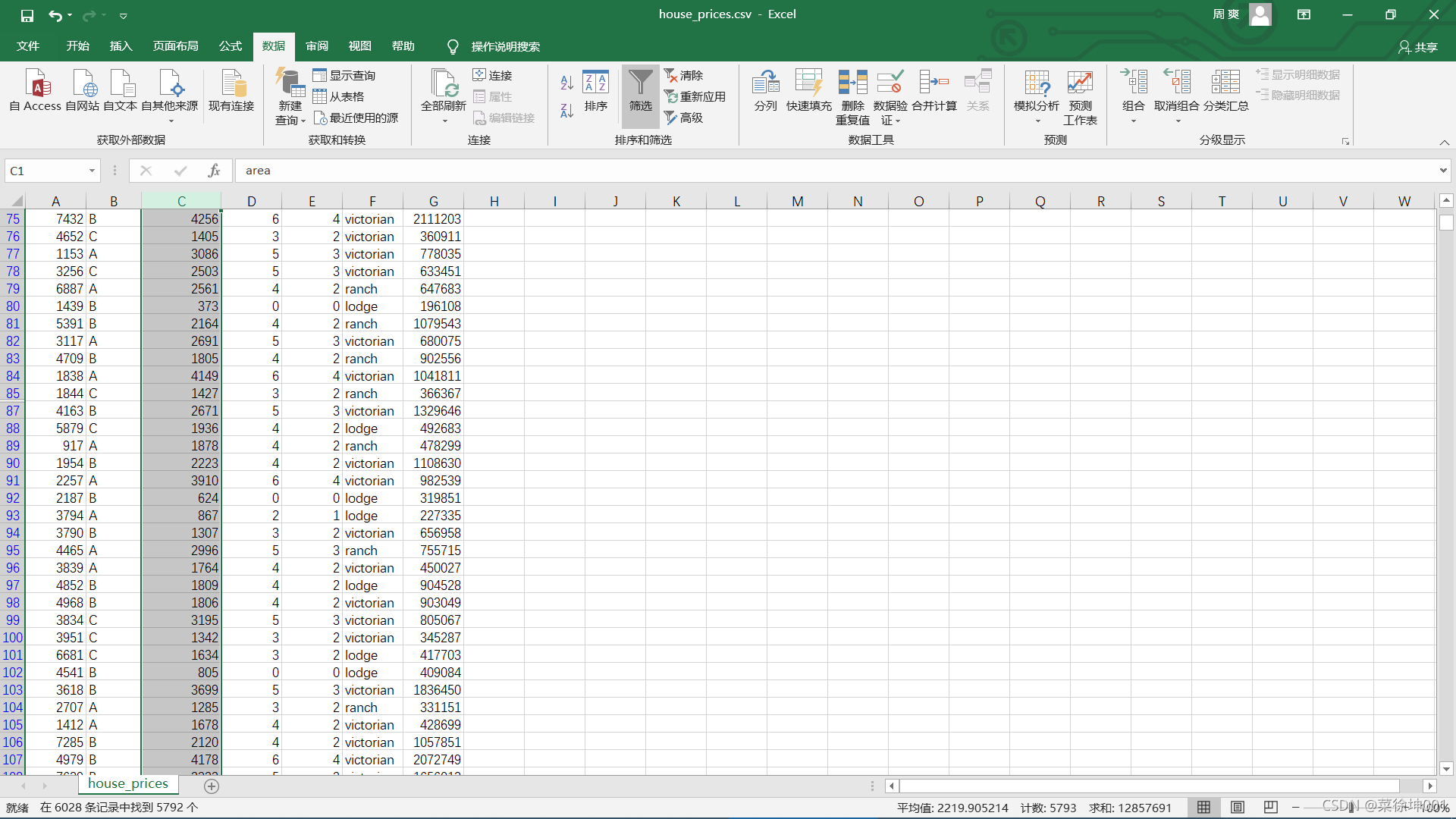
3、非数值型数据转换

对于style，将原数据的ranch、victorian、lodge替换为100、200、300。
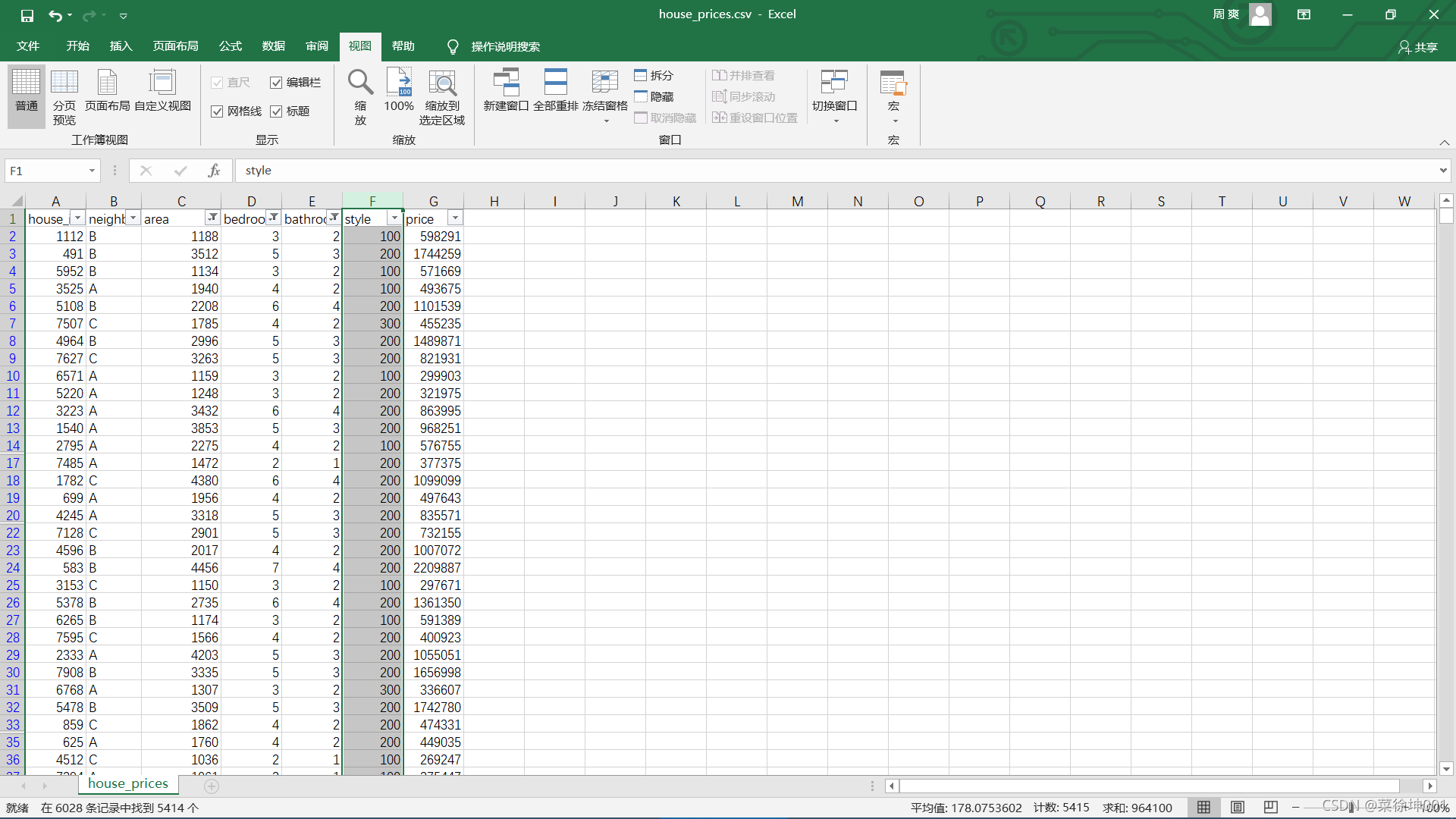
在这里插入图片描述
这样就可以进行线性回归了。

四、使用Excel实现回归

1.回归实现

将房价(price)作为因变量，表格中的其他变量作为自变量，使用Excel对表中的数据进行回归分析。
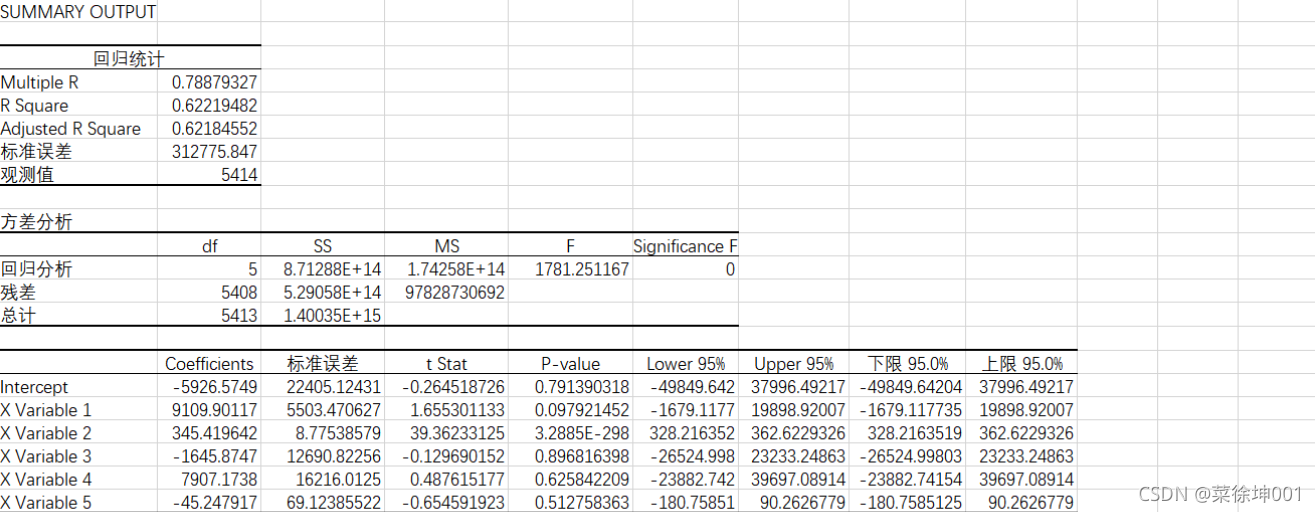
在这里插入图片描述

2、回归分析

在这里插入图片描述
但根据Coefficients估算出的回归方程可能存在较大的误差。更为重要的是P-value值，由表中P-value的值可以发现，自变量房屋面积x 2 x_2x
2
?
的P值远小于显著性水平0.05，因此房屋面积(area)与房价(price)相关。卧室数(bedrooms)和浴室数(bathrooms)的P值远大于显著性水平0.05，说明这卧室数(bedrooms)和浴室数(bathrooms)与房价(price)相关性较弱，甚至不存在线性相关关系。

五、使用代码实现回归

数据预处理

首先查看数据的基础信息

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt#导入数据
df = pd.read_csv("house_prices.csv")
#读取数据的基础信息
df.info()

在这里插入图片描述
df.info():返回表格的一些基本信息，主要介绍数据集各列的数据类型，是否为空值，内存占用情况
RangeIndex: # 行数，5414行
Data columns (total 7 columns): #列数，7列
non-null: 意思为非空的数据
dtypes: int64(5), object(2) :数据类型
2、冗余数据的判断与处理

# 判断数据中是否存在重复观测
df.duplicated().any()

3、缺失值识别与处理

# 判断各变量中是否存在缺失值
df.isnull().any(axis = 0)
# 各变量中缺失值的数量
df.isnull().sum(axis = 0)
# 各变量中缺失值的比例
df.isnull().sum(axis = 0)/df.shape[0]

在这里插入图片描述
4、数据异常值识别与处理

# 异常值处理
# ================ 异常值检验函数：iqr & z分数 两种方法 =========================
def outlier_test(data, column, method=None, z=2):
    """ 以某列为依据，使用 上下截断点法 检测异常值(索引) """
    """ 
    full_data: 完整数据
    column: full_data 中的指定列，格式 'x' 带引号
    return 可选; outlier: 异常值数据框 
    upper: 上截断点;  lower: 下截断点
    method：检验异常值的方法（可选, 默认的 None 为上下截断点法），
            选 Z 方法时，Z 默认为 2
    """
    # ================== 上下截断点法检验异常值 ==============================
    if method == None:
        print(f'以 {column} 列为依据，使用 上下截断点法(iqr) 检测异常值...')
        print('=' * 70)
        # 四分位点；这里调用函数会存在异常
        column_iqr = np.quantile(data[column], 0.75) - np.quantile(data[column], 0.25)
        # 1，3 分位数
        (q1, q3) = np.quantile(data[column], 0.25), np.quantile(data[column], 0.75)
        # 计算上下截断点
        upper, lower = (q3 + 1.5 * column_iqr), (q1 - 1.5 * column_iqr)
        # 检测异常值
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        print(f'第一分位数: {q1}, 第三分位数：{q3}, 四分位极差：{column_iqr}')
        print(f"上截断点：{upper}, 下截断点：{lower}")
        return outlier, upper, lower
    # ===================== Z 分数检验异常值 ==========================
    if method == 'z':
        """ 以某列为依据，传入数据与希望分段的 z 分数点，返回异常值索引与所在数据框 """
        """ 
        params
        data: 完整数据
        column: 指定的检测列
        z: Z分位数, 默认为2，根据 z分数-正态曲线表，可知取左右两端的 2%，
           根据您 z 分数的正负设置。也可以任意更改，知道任意顶端百分比的数据集合
        """
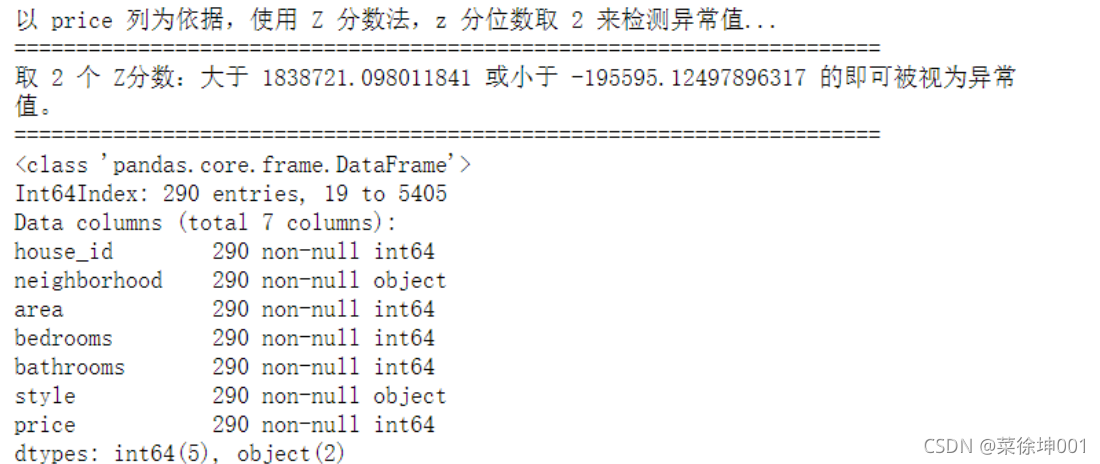
        print(f'以 {column} 列为依据，使用 Z 分数法，z 分位数取 {z} 来检测异常值...')
        print('=' * 70)
        # 计算两个 Z 分数的数值点
        mean, std = np.mean(data[column]), np.std(data[column])
        upper, lower = (mean + z * std), (mean - z * std)
        print(f"取 {z} 个 Z分数：大于 {upper} 或小于 {lower} 的即可被视为异常值。")
        print('=' * 70)
        # 检测异常值
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        return outlier, upper, lower

进行异常检测‘

#对数据进行异常值检测
outlier, upper, lower = outlier_test(data=df, column='price', method='z')

outlier.info();
outlier.sample(5)

在这里插入图片描述
丢弃异常值

# 这里简单的丢弃即可
df.drop(index=outlier.index, inplace=True)

5、统计非数值变量

# 类别变量，又称为名义变量，nominal variables
nominal_vars = ['neighborhood', 'style']

for each in nominal_vars:
    print(each, ':')
    print(df[each].agg(['value_counts']).T)
    # 直接 .value_counts().T 无法实现下面的效果
    ## 必须得 agg，而且里面的中括号 [] 也不能少
    print('='*35)
    # 发现各类别的数量也都还可以，为下面的方差分析做准备

在这里插入图片描述
绘出热力图

# 热力图 
def heatmap(data, method='pearson', camp='RdYlGn', figsize=(10 ,8)):
    """
    data: 整份数据
    method：默认为 pearson 系数
    camp：默认为：RdYlGn-红黄蓝；YlGnBu-黄绿蓝；Blues/Greens 也是不错的选择
    figsize: 默认为 10，8
    """
    ##    消除斜对角颜色重复的色块
    #     mask = np.zeros_like(df2.corr())
    #     mask[np.tril_indices_from(mask)] = True
    plt.figure(figsize=figsize, dpi= 80)
    sns.heatmap(data.corr(method=method), \
                xticklabels=data.corr(method=method).columns, \
                yticklabels=data.corr(method=method).columns, cmap=camp, \
                center=0, annot=True)
    # 要想实现只是留下对角线一半的效果，括号内的参数可以加上 mask=mask

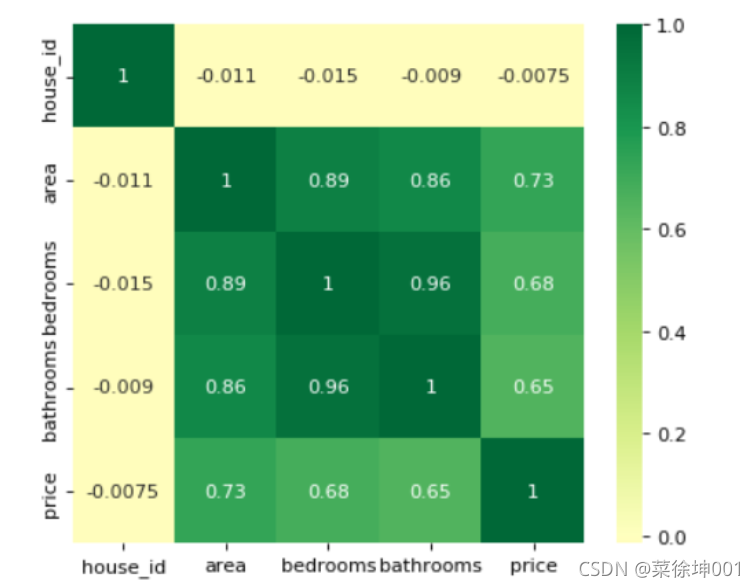
在这里插入图片描述
?通过热力图可以看出 area，bedrooms，bathrooms等变量与房屋价格 price 的关系都还比较强，所以值得放入模型，但分类变量 style与 neighborhood 两者与 price 的关系未知。
?5、方差分析

## 利用回归模型中的方差分析
## 只有 statsmodels 有方差分析库
## 从线性回归结果中提取方差分析结果
import statsmodels.api as sm
from statsmodels.formula.api import ols # ols 为建立线性回归模型的统计学库
from statsmodels.stats.anova import anova_lm

# 从数据集样本中随机选择 600 条，如果希望分层抽样，可参考文章：
df = df.copy().sample(600)

# C 表示告诉 Python 这是分类变量，否则 Python 会当成连续变量使用
## 这里直接使用方差分析对所有分类变量进行检验
## 下面几行代码便是使用统计学库进行方差分析的标准姿势
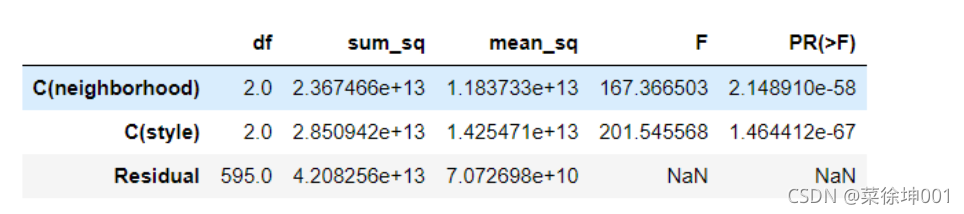
lm = ols('price ~ C(neighborhood) + C(style)', data=df).fit()
anova_lm(lm)

# Residual 行表示模型不能解释的组内的，其他的是能解释的组间的
# df: 自由度（n-1）- 分类变量中的类别个数减1
# sum_sq: 总平方和（SSM），residual行的 sum_eq: SSE
# mean_sq: msm, residual行的 mean_sq: mse
# F：F 统计量，查看卡方分布表即可
# PR(>F): P 值

在这里插入图片描述

使用Statsmodels建立多元线性回归模型

此处直接使用最小二乘法建立线性回归模型

from statsmodels.formula.api import ols
#最小二乘法建立线性回归模型
lm = ols('price ~ area + bedrooms + bathrooms', data=df).fit()
lm.summary()

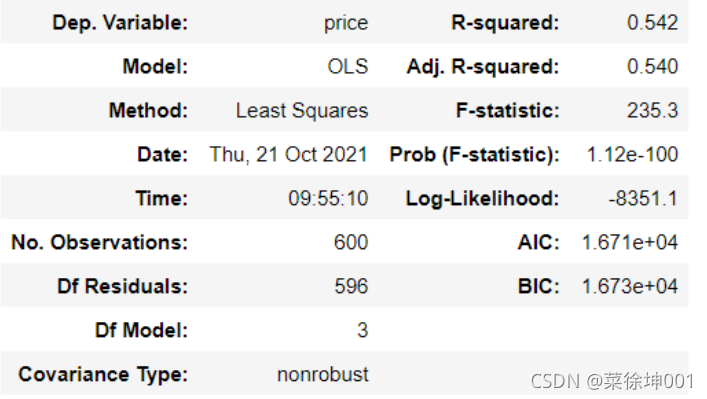
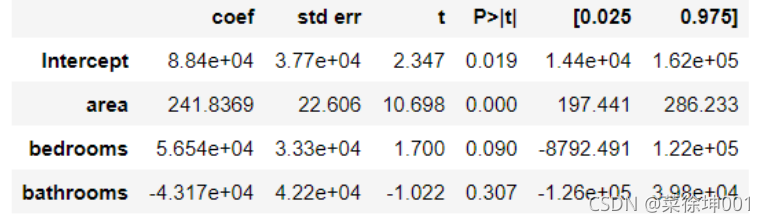
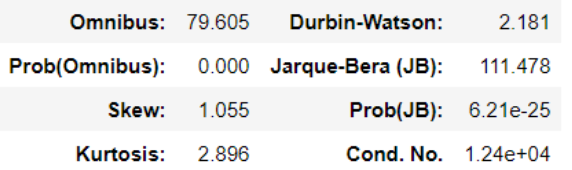
在这里插入图片描述

模型拟合效果不理想，R 2 = 0.54 R^2 =0.54R
2
=0.54，模型需要进一步优化。

使用Sklearn库建立多元线性回归模型

#导入相关库
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split #这里是引用了交叉验证
from sklearn.linear_model import LinearRegression  #线性回归
from sklearn.linear_model import Lasso, Ridge, LinearRegression as LR
from sklearn.metrics import r2_score, explained_variance_score as EVS, mean_squared_error as MSE
from sklearn.model_selection import train_test_split, cross_val_score
from pandas.core.accessor import register_dataframe_accessor

#读入数据
data=pd.read_csv('house_prices.csv')
x = data[['neighborhood','area','bedrooms','bathrooms','style']]# 特征数据，自变量
y= data['price']# 标签值，因变量

#以8：2的比例分成训练集与测试集
x_train, x_test, y_train, y_test = train_test_split(
    x, y, test_size=0.2, random_state=1)

reg = LR().fit(x_train, y_train)  # 训练模型
yhat = reg.predict(x_test)  # 基于测试集x去预测标签
print("r2 = ",r2_score(y_test,yhat))#判定系数R^2

在这里插入图片描述

f = open("多元线性回归.txt", 'w+', encoding='utf8')
f.write("参数为：" + str(reg.coef_)+"\t\n")  # 得到各个特征的系数
f.write("截距为：" + str(reg.intercept_)+"\t\n")  # 得到截距，常数c
f.write("均方差为：" + str(MSE(y_test, yhat))+"\t\n")  # 均方差（绝对值）
f.write('平均误差相对于样本真实值平均值的比例为：'+str(np.sqrt(MSE(y_test, yhat)) /y_test.mean())+"\t\n")  # 平均误差相对于样本真实值平均值的比例
f.write("判定系数R^2为："+str(r2_score(y_test,yhat))+"\t\n")
#print("R^2的均值为：",r2_score(y_test,yhat))
f.write(("可解释方差为："+str(cross_val_score(reg, x, y, cv=5, scoring="explained_variance")) ))
f.close()