算法简介
聚类算法是一种无监督学习,简单来讲就是依靠样本间聚类通过不断迭代聚类中心的方式来完成样本聚类。常见的单层聚类方式有K-means聚类和FCM聚类等。
K-means算法简介
K-means是一种硬聚类方式,即确定的将每个样本分入一个确定的聚类簇中。它的实现方式就是迭代更新聚类中心,具体而言,首先初始化 k k k个聚类中心,然后将每个样本归到与自己距离最近的聚类中心上,再重新计算聚类中心,如此反复迭代直至算法达到停止条件。
FCM算法简介
FCM与k-means相比,是一种模糊聚类的方法,即最终的聚类结果为一隶属度矩阵,记录每个样本隶属于每个聚类簇的隶属度。具体的实现方式与k-means也类似,首先可以初始化隶属度矩阵,然后依靠迭代公式确定聚类中心,再迭代更新隶属度矩阵,如此迭代直至达到停止条件。
显然,K-means算法和FCM算法的效果很大程度上取决于 k k k值的选择。但对于有标签数据集进行实验时,一般可以选择其类别数作为 k k k值实验。
算法流程
首先声明符号。记 X = { x i j } n × m X=\left\{x_{ij}\right\}_{n\times m} X={xij?}n×m?表示样本矩阵,其中 n n n表示样本数量, m m m表示样本维数。记类别标签为 C = { C 1 , C 2 , … , C k } C=\left\{C_1,C_2,\ldots, C_k\right\} C={C1?,C2?,…,Ck?}表示 k k k个类别,亦即聚类簇。
K-means算法流程
K-means的目标是最小化
J
=
∑
i
=
1
k
J
i
=
∑
i
=
1
k
∑
x
∈
C
i
∣
∣
x
?
m
i
∣
∣
J = \sum_{i=1}^{k} J_i = \sum_{i=1}^{k}\sum_{\boldsymbol{x} \in C_i} \Big|\Big|\boldsymbol{x}-\boldsymbol{m}_i\Big|\Big|
J=i=1∑k?Ji?=i=1∑k?x∈Ci?∑?∣∣∣?∣∣∣?x?mi?∣∣∣?∣∣∣?
其中
x
\boldsymbol{x}
x表示样本向量,
m
1
,
m
2
,
…
,
m
k
\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_k
m1?,m2?,…,mk?表示
C
1
,
C
2
,
…
,
C
k
C_1, C_2, \ldots, C_k
C1?,C2?,…,Ck?的聚类中心向量,计算公式为
m
i
=
1
∣
C
i
∣
∑
x
∈
C
i
x
\boldsymbol{m}_i = \frac{1}{\left|C_i\right|}\sum_{\boldsymbol{x} \in C_i} \boldsymbol{x}
mi?=∣Ci?∣1?x∈Ci?∑?x
其中
∣
C
i
∣
\left|C_i\right|
∣Ci?∣表示类
C
i
C_i
Ci?的大小。
在此基础上,给出k-means的算法流程:
- 初始化选择 k k k个聚类中心 m 1 ( 1 ) , m 2 ( 1 ) , … , m k ( 1 ) \boldsymbol{m}_1^{(1)}, \boldsymbol{m}_2^{(1)}, \ldots, \boldsymbol{m}_k^{(1)} m1(1)?,m2(1)?,…,mk(1)?,可以完全随机选取或选取若干样本点。并记 t = 1 t=1 t=1表示当前迭代次数。
- 根据最小距离标准将要分类的模式样本
x
\boldsymbol{x}
x分配给
k
k
k个簇中的某一个
C
i
C_i
Ci?。若
j = arg ? max ? i { ∣ ∣ x ? m i ( t ) ∣ ∣ , ?? i = 1 , 2 , … , k } j = \mathop{\arg\max}_i \left\{\left|\left|\boldsymbol{x} - \boldsymbol{m}_i^{(t)} \right|\right|,\; i=1,2,\ldots,k \right\} j=argmaxi?{∣∣∣?∣∣∣?x?mi(t)?∣∣∣?∣∣∣?,i=1,2,…,k}
则 x ∈ C j ( t ) \boldsymbol{x}\in C_j^{(t)} x∈Cj(t)?,即 x \boldsymbol{x} x属于聚类 C j ( t ) C_j^{(t)} Cj(t)?。 - 计算各个聚类中心的新的向量值
m
i
(
t
+
1
)
\boldsymbol{m}_i^{(t+1)}
mi(t+1)?,即
m i ( t + 1 ) = 1 ∣ C i ∣ ∑ x ∈ C i x , ?? i = 1 , 2 , … , k \boldsymbol{m}_i^{(t+1)} = \frac{1}{\left|C_i\right|}\sum_{\boldsymbol{x} \in C_i} \boldsymbol{x},\; i=1,2,\ldots, k mi(t+1)?=∣Ci?∣1?x∈Ci?∑?x,i=1,2,…,k - 若 m i ( t + 1 ) ≠ m i ( t ) , ?? i = 1 , 2 , … , k \boldsymbol{m}_i^{(t+1)} \neq \boldsymbol{m}_i^{(t)},\; i=1,2,\ldots,k mi(t+1)??=mi(t)?,i=1,2,…,k,则算法仍未收敛,返回步骤2。否则,算法收敛,返回 { C 1 , C 2 , … , C k } \left\{C_1,C_2,\ldots, C_k\right\} {C1?,C2?,…,Ck?}和 { m 1 , m 2 , … , m k } \left\{\boldsymbol{m}_1, \boldsymbol{m}_2, \ldots, \boldsymbol{m}_k\right\} {m1?,m2?,…,mk?},算法结束。
FCM算法流程
FCM的目标是最小化
J
=
∑
j
=
1
k
∑
i
=
1
n
[
μ
j
(
x
i
)
]
b
∣
∣
x
i
?
m
j
∣
∣
2
=
∑
j
=
1
k
∑
i
=
1
n
μ
i
j
b
??
d
i
j
\begin{aligned} J &= \sum_{j=1}^{k}\sum_{i=1}^{n}\Big[\mu_j(\boldsymbol{x}_i)\Big]^b \Big|\Big|\boldsymbol{x}_i - \boldsymbol{m}_j \Big|\Big|^2\\ &= \sum_{j=1}^{k}\sum_{i=1}^{n}\mu_{ij}^b\;d_{ij} \end{aligned}
J?=j=1∑k?i=1∑n?[μj?(xi?)]b∣∣∣?∣∣∣?xi??mj?∣∣∣?∣∣∣?2=j=1∑k?i=1∑n?μijb?dij??
其中,与前类似,
x
i
\boldsymbol{x}_i
xi?表示样本,
m
j
\boldsymbol{m}_j
mj?表示聚类中心,而
μ
j
(
x
i
)
=
μ
i
j
\mu_j(\boldsymbol{x}_i)=\mu_{ij}
μj?(xi?)=μij?表示样本
x
i
\boldsymbol{x}_i
xi?隶属于聚类
C
j
C_j
Cj?的隶属度,
b
b
b为模糊常数,记号
d
i
j
d_{ij}
dij?表示样本
x
i
\boldsymbol{x}_i
xi?与类
C
j
C_j
Cj?中心
m
j
\boldsymbol{m}_j
mj?之间的距离。
作为隶属度,显然
μ
i
j
\mu_{ij}
μij?要满足
∑
j
=
1
k
μ
i
j
=
1
,
??
i
=
1
,
2
,
…
,
n
\sum_{j=1}^{k}\mu_{ij}=1,\; i=1,2,\ldots,n
j=1∑k?μij?=1,i=1,2,…,n
即同一个样本隶属于
k
k
k个聚类簇的隶属度之和应为1。
由此约束条件,使用拉格朗日乘子法求解极小值。得到
m
j
=
∑
i
=
1
n
μ
i
j
b
??
x
i
∑
i
=
1
n
μ
i
j
b
,
????
μ
i
j
=
(
1
/
d
i
j
)
1
/
(
b
?
1
)
∑
l
=
1
k
(
1
/
d
i
l
)
1
/
(
b
?
1
)
=
1
∑
l
=
1
k
(
d
i
j
/
d
i
l
)
1
/
(
b
?
1
)
\boldsymbol{m}_j = {\displaystyle{\frac{\displaystyle{\sum_{i=1}^{n}\mu_{ij}^b\; \boldsymbol{x}_i}}{\displaystyle{\sum_{i=1}^{n}\mu_{ij}^b}}}},\;\; \mu_{ij}= {\displaystyle{\frac{\displaystyle{\left(1\big/ d_{ij}\right)^{1/(b-1)}}}{\displaystyle{\sum_{l=1}^{k}\left(1\big/ d_{il}\right)^{1/(b-1)}}}}} = {\displaystyle{\frac{\displaystyle{1}}{\displaystyle{\sum_{l=1}^{k}(d_{ij} / d_{il})^{1/(b-1)}}}}}
mj?=i=1∑n?μijb?i=1∑n?μijb?xi??,μij?=l=1∑k?(1/dil?)1/(b?1)(1/dij?)1/(b?1)?=l=1∑k?(dij?/dil?)1/(b?1)1?
下面给出FCM算法的流程:
- 初始化隶属度矩阵 U ( 0 ) = { μ i j ( 0 ) } U^{(0)}=\left\{\mu_{ij}^{(0)}\right\} U(0)={μij(0)?},并记迭代次数 t = 0 t=0 t=0。
- 根据下式更新聚类中心
m
(
t
+
1
)
\boldsymbol{m}^{(t+1)}
m(t+1)
m j ( t + 1 ) = ∑ i = 1 n [ μ i j ( t ) ] b x i ∑ i = 1 n [ μ i j ( t ) ] b \boldsymbol{m}_j^{(t+1)} = {\displaystyle{\frac{\displaystyle{\sum_{i=1}^{n}\left[\mu_{ij}^{(t)}\right]^b\boldsymbol{x}_i}}{\displaystyle{\sum_{i=1}^{n}\left[\mu_{ij}^{(t)}\right]^b}}}} mj(t+1)?=i=1∑n?[μij(t)?]bi=1∑n?[μij(t)?]bxi?? - 根据下式更新隶属度矩阵
U
(
t
+
1
)
U^{(t+1)}
U(t+1)
μ i j ( t + 1 ) = 1 ∑ l = 1 k [ d i j ( t + 1 ) / d i l ( t + 1 ) ] 1 / ( b ? 1 ) \mu_{ij}^{(t+1)} = {\displaystyle{\frac{\displaystyle{1}}{\displaystyle{\sum_{l=1}^{k}\left[d_{ij}^{(t+1)} / d_{il}^{(t+1)}\right]^{1/(b-1)}}}}} μij(t+1)?=l=1∑k?[dij(t+1)?/dil(t+1)?]1/(b?1)1?
其中与上类似, d i j ( t ) = ∣ ∣ x i ? m j ( t ) ∣ ∣ 2 d_{ij}^{(t)}=\left|\left|\boldsymbol{x}_i - \boldsymbol{m}_j^{(t)} \right|\right|^2 dij(t)?=∣∣∣?∣∣∣?xi??mj(t)?∣∣∣?∣∣∣?2。 - 根据下式更新聚类中心
m
(
t
+
1
)
\boldsymbol{m}^{(t+1)}
m(t+1)
若 ∣ ∣ m ( t ) ? m ( t + 1 ) ∣ ∣ < ε \Big|\Big| \boldsymbol{m}^{(t)} -\boldsymbol{m}^{(t+1)} \Big|\Big| < \varepsilon ∣∣∣?∣∣∣?m(t)?m(t+1)∣∣∣?∣∣∣?<ε,则表示算法收敛,停止迭代,输出 m \boldsymbol{m} m以及 U U U。否则,返回步骤3。
数据集介绍
UCI-sonar数据集
UCI-sonar数据集是一个通过声纳数据对岩石和水雷判别的数据集。其只有两类“M”和“R”表示水雷和岩石,样本空间60维,为60个声纳点的收集数据,数据集共有207个样本,其中111个“M”类,96个“R”类。
UCI-iris数据集
UCI-iris数据集是一个分类鸢尾花的数据集,共有四个类别,样本空间为四维,表示花的四个特征,数据集共有150个样本。
Cifar-10数据集
Cifar-10数据集是一个图像分类数据集,图像尺寸 3 × 32 × 32 3\times 32 \times 32 3×32×32,共10类。本次实验使用单张图片的所有像素点作为数据集,进行类似图像分割的聚类任务。

实验设置
对于前两个数据集,均使用其原本的类别数作为 k k k值。对于Cifar-10数据集,尝试多个不同的k值实验。而FCM的聚类参数 b b b,统一取1.1。
实验环境:Intel? Core? i7-9750H CPU @ 2.60GHz.
Python版本:python3.6, numpy=1.19.4, sklearn=0.21.2.
实验结果及分析
聚类实验
首先使用两个算法在UCI的两个数据集上进行实验。下面两图截取数据集的前两维做展示。
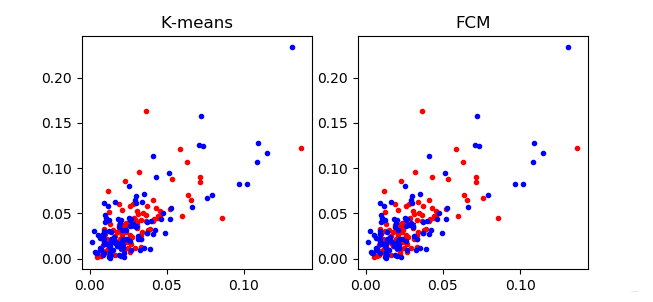

可以看出,仅靠前两个维度iris数据集就已经基本可分,聚类效果较好。但sonars数据集可分性较差。当然,仅靠前两个维度无法对算法的总体效果下定论,尤其是sonars数据集有60个维度。因此,引入三个常用的聚类算法评价指标。在此不赘述指标的具体计算及实现方式,仅做简单说明,
ARI指标
ARI指标是一种需要数据集标签的分类指标,指标范围在 [ ? 1 , ?? 1 ] [-1,\; 1] [?1,1],越大表示聚类结果与原标签越接近,即聚类效果越好。
FMI指标
FMI指标也需要有标签数据,与AR指标比较类似,但指标范围在 [ 0 , ?? 1 ] [0,\; 1] [0,1]之间,越大聚类效果越好。
SC指标
SC指标是一种衡量聚类簇间和内部距离的指标,因此其不需要有标签数据。指标范围在 [ 0 , ?? 1 ] [0, \; 1] [0,1]之间,也是指标越大表示聚类效果越好。
实验两个数据集在两个算法下的表现,得到下表的数据
| UCI-sonar | UCI-iris | |||
|---|---|---|---|---|
| K-means | FCM | K-means | FCM | |
| Time/ms | 6.2 | 7.1 | 1.3 | 2.0 |
| ARI | 0.002 | 0.008 | 0.716 | 0.730 |
| FMI | 0.505 | 0.503 | 0.811 | 0.821 |
| SC | 0.199 | 0.198 | 0.551 | 0.552 |
从上表易得,FCM在两个数据集上得表现都略优于K-means算法,而相应的要有更大的时间开销。同时,sonars数据集的聚类效果明显不如iris数据集,甚至接近随机分类。
图像分割实验
使用两种算法对单张图像中的像素点进行聚类,即数据集为一张图片,样本点 32 × 32 32\times 32 32×32个,维度为3维(RGB)。初步实验结果如下图,第一张为原图,Mask图片从左到右每两张依次是 k = 3 , 4 , 5 , 6 k=3,4,5,6 k=3,4,5,6,两张中左侧为k-means,右侧为FCM。

显然这样的聚类完全基于像素点的颜色,效果很差,几乎完全没有达到图像分割的目的。
考虑到,图像分割的结果是与像素点的空间位置有关的,因此尝试加入两个数据维度表示像素点的 x x x与 y y y方向坐标,以此表征两个像素点的空间位置关系。显然,两个在图像上距离相近的像素点,在新的数据维度上也是同样的相近。
对于新的5维数据集,再做聚类,此时效果已经明显改善。这里展示9张图片。

总体来看,这样的分割效果比较理想,但是并不是针对特定目标的分割,而仍是对相似色块的分割。两种算法对比来看,FCM算法与k-means并无太大差异。
附录
附录总体为代码。首先是我编写的k-means以及FCM类,然后是在三个数据集上的实验。
类
import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
from scipy.spatial.distance import cdist
from sklearn import datasets, metrics
import time
class KMeans(BaseEstimator, ClassifierMixin):
def __init__(self, k):
# method=2 => use L2 distance
self.k = k
self.x = None
self.y = None
self.labels = None
self.centers = None
self.iterations = 500
def quick_L2(self, x, a):
"""
Calculate distance between every vectors in x and a.
:param x: (n, n_features)
:param a: (m, n_features)
:return: (n, m) distance between every vectors in x and a
"""
dis = -2 * np.dot(x, a.T)
dis += np.einsum('ij,ij->i', x, x)[:, np.newaxis]
dis += np.einsum('ij,ij->i', a, a)[np.newaxis, :]
return dis
def fit(self, x, y=None, init_method='random_point', seed=None, eps=1e-5):
self.x = x
self.y = y
self.centers = 0
if seed is not None:
np.random.seed(seed)
if init_method == 'random_point':
self.centers = x[np.random.choice(x.shape[0], self.k), :]
else:
self.centers = np.random.randint(np.min(x), np.max(x), (x.shape[0], self.k))
pre_centers = self.centers.copy()
for i in range(self.iterations):
dis = self.quick_L2(self.x, self.centers)
idx = np.argmin(dis, axis=1)
for j in range(self.centers.shape[0]):
self.centers[j, :] = np.mean(self.x[idx == j, :], axis=0)
if np.mean(np.abs(pre_centers - self.centers)) < eps:
break
pre_centers = self.centers.copy()
def predict(self, a=None):
if a is None:
a = self.x
dis = self.quick_L2(a, self.centers)
idx = np.argmin(dis, axis=1)
return idx
class FCM(BaseEstimator, ClassifierMixin):
def __init__(self, k, alpha=2):
# method=2 => use L2 distance
self.k = k
self.alpha = alpha
self.x = None
self.y = None
self.labels = None
self.centers = None
self.u = None
self.iterations = 500
def quick_L2(self, x, a):
"""
Calculate distance between every vectors in x and a.
:param x: (n, n_features)
:param a: (m, n_features)
:return: (n, m) distance between every vectors in x and a
"""
dis = -2 * np.dot(x, a.T)
dis += np.einsum('ij,ij->i', x, x)[:, np.newaxis]
dis += np.einsum('ij,ij->i', a, a)[np.newaxis, :]
return dis
def fit(self, x, y=None, init_method='u', seed=None, eps=1e-5):
self.x = x
self.y = y
if seed is not None:
np.random.seed(seed)
if init_method == 'u':
self.u = np.random.rand(self.x.shape[0], self.k)
self.u /= np.sum(self.u, axis=1)[:, np.newaxis]
else:
# TODO
pass
pre_J = 0
for i in range(self.iterations):
u_a = self.u ** self.alpha # u_{ij}^{\alpha}
self.centers = np.dot(self.u.T, self.x) / np.sum(self.u, axis=0)[:, np.newaxis]
dis = self.quick_L2(self.x, self.centers)
J = np.sum(u_a * dis)
if abs(J - pre_J) < eps:
return
# Ensure \alpha - 1 != 0.
# Note that dis_ij is for d_ij^2
e = 1 / (self.alpha - 1 + eps * 100)
self.u = 1 / ((dis ** e) * np.sum(dis ** (-e), axis=1)[:, np.newaxis])
pre_J = J
def predict(self):
return np.argmax(self.u, axis=1)
if __name__ == '__main__':
iris = datasets.load_iris()
data = iris['data']
labels = iris['target']
tim = time.clock()
print('KNN:')
kmeans = KMeans(k=3)
kmeans.fit(data)
res = kmeans.predict()
print(res)
print('Time: ' + str(time.clock() - tim))
print('ARI指标: ' + str(metrics.adjusted_rand_score(labels, res)))
print('FMI指标: ' + str(metrics.fowlkes_mallows_score(labels, res)))
print('SC指标: ' + str(metrics.silhouette_score(data, res, metric='euclidean')))
print('----------------------------------------')
tim = time.clock()
print('FCM:')
fcm = FCM(k=3)
fcm.fit(data)
res = fcm.predict()
print(res)
print('Time: ' + str(time.clock() - tim))
print('ARI指标: ' + str(metrics.adjusted_rand_score(labels, res)))
print('FMI指标: ' + str(metrics.fowlkes_mallows_score(labels, res)))
print('SC指标: ' + str(metrics.silhouette_score(data, res, metric='euclidean')))
.
sonars实验
from module import FCM, KMeans
from sklearn import metrics
import time
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
path = 'sonar.all-data'
data = pd.read_csv(path).values
labels = np.zeros_like(data[:, -1])
labels[data[:, -1] == 'R'] = 1
data = np.asarray(data[:, :-1], dtype=np.float32)
tim = time.clock()
print('KNN:')
kmeans = KMeans(k=2)
kmeans.fit(data)
res = kmeans.predict()
print(res)
print('Time: ' + str(time.clock() - tim))
print('ARI指标: ' + str(metrics.adjusted_rand_score(labels, res)))
print('FMI指标: ' + str(metrics.fowlkes_mallows_score(labels, res)))
print('SC指标: ' + str(metrics.silhouette_score(data, res, metric='euclidean')))
plt.subplot(121)
plt.title('K-means')
plt.plot(data[res == 0, 0], data[res == 0, 1], 'r.')
plt.plot(data[res == 1, 0], data[res == 1, 1], 'b.')
plt.plot(kmeans.centers[0, 0], kmeans.centers[0, 1], 'r*')
plt.plot(kmeans.centers[1, 0], kmeans.centers[1, 1], 'b*')
print('----------------------------------------')
tim = time.clock()
print('FCM:')
fcm = FCM(k=2)
fcm.fit(data)
res = fcm.predict()
print(res)
print('Time: ' + str(time.clock() - tim))
print('ARI指标: ' + str(metrics.adjusted_rand_score(labels, res)))
print('FMI指标: ' + str(metrics.fowlkes_mallows_score(labels, res)))
print('SC指标: ' + str(metrics.silhouette_score(data, res, metric='euclidean')))
plt.subplot(122)
plt.title('FCM')
plt.plot(data[res == 0, 0], data[res == 0, 1], 'r.')
plt.plot(data[res == 1, 0], data[res == 1, 1], 'b.')
plt.plot(fcm.centers[0, 0], fcm.centers[0, 1], 'r*')
plt.plot(fcm.centers[1, 0], fcm.centers[1, 1], 'b*')
plt.show()
.
iris实验
from module import FCM, KMeans
from sklearn import datasets, metrics
import time
import matplotlib.pyplot as plt
iris = datasets.load_iris()
data = iris['data']
labels = iris['target']
tim = time.clock()
print('KNN:')
kmeans = KMeans(k=3)
kmeans.fit(data)
res = kmeans.predict()
print(res)
print('Time: ' + str(time.clock() - tim))
print('ARI指标: ' + str(metrics.adjusted_rand_score(labels, res)))
print('FMI指标: ' + str(metrics.fowlkes_mallows_score(labels, res)))
print('SC指标: ' + str(metrics.silhouette_score(data, res, metric='euclidean')))
plt.subplot(121)
plt.title('K-means')
plt.plot(data[res == 0, 0], data[res == 0, 1], 'r.')
plt.plot(data[res == 1, 0], data[res == 1, 1], 'b.')
plt.plot(data[res == 2, 0], data[res == 2, 1], 'y.')
plt.plot(kmeans.centers[0, 0], kmeans.centers[0, 1], 'r*')
plt.plot(kmeans.centers[1, 0], kmeans.centers[1, 1], 'b*')
plt.plot(kmeans.centers[2, 0], kmeans.centers[2, 1], 'y*')
print('----------------------------------------')
tim = time.clock()
print('FCM:')
fcm = FCM(k=3)
fcm.fit(data)
res = fcm.predict()
print(res)
print('Time: ' + str(time.clock() - tim))
print('ARI指标: ' + str(metrics.adjusted_rand_score(labels, res)))
print('FMI指标: ' + str(metrics.fowlkes_mallows_score(labels, res)))
print('SC指标: ' + str(metrics.silhouette_score(data, res, metric='euclidean')))
plt.subplot(122)
plt.title('FCM')
plt.plot(data[res == 0, 0], data[res == 0, 1], 'r.')
plt.plot(data[res == 1, 0], data[res == 1, 1], 'b.')
plt.plot(data[res == 2, 0], data[res == 2, 1], 'y.')
plt.plot(fcm.centers[0, 0], fcm.centers[0, 1], 'r*')
plt.plot(fcm.centers[1, 0], fcm.centers[1, 1], 'b*')
plt.plot(fcm.centers[2, 0], fcm.centers[2, 1], 'y*')
plt.show()
.
CIFAR实验
from module import FCM, KMeans
import numpy as np
import cv2
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
def unpickle(file):
import pickle
with open(file, 'rb') as fo:
dic = pickle.load(fo, encoding='bytes')
return dic
def put_mask(img, mask):
mask_draw = np.zeros((32, 32, 3), dtype=np.uint8)
mask_draw[mask == 0] = np.array((0, 0, 255))
mask_draw[mask == 1] = np.array((0, 255, 0))
mask_draw[mask == 2] = np.array((255, 0, 0))
mask_draw[mask == 3] = np.array((255, 255, 0))
mask_draw[mask == 4] = np.array((255, 0, 255))
mask_draw[mask == 5] = np.array((0, 255, 255))
mask_draw[mask == 6] = np.array((0, 0, 0))
# alpha 为第一张图片的透明度
alpha = 0.8
# beta 为第二张图片的透明度
beta = 0.2
gamma = 0
# cv2.addWeighted 将原始图片与 mask 融合
masked_img = cv2.addWeighted(img, alpha, mask_draw, beta, gamma)
return mask_draw, masked_img
if __name__ == '__main__':
pic_list = range(1,10)
k_list = [3, 4, 5, 6]
ttt = 0 # num for showing pictures
plt.figure(1)
for i in range(len(pic_list)):
img = cv2.imread(str(pic_list[i]) + '.jpg')
print(img.shape)
ttt += 1
plt.subplot(len(pic_list), len(k_list) * 2 + 1, ttt)
plt.axis('off')
plt.imshow(img)
if i == 0:
plt.title('原图', fontdict={'fontsize': 10})
for kk in range(len(k_list)):
tmp = [img[:, :, i].reshape((1024, 1)) for i in range(3)]
tmp.append(np.array([i % 32 for i in range(1024)]).reshape(1024, 1))
tmp.append(np.array([i // 32 for i in range(1024)]).reshape(1024, 1))
data = np.concatenate(tmp, axis=1)
kmeans = KMeans(k=k_list[kk])
kmeans.fit(data)
label = kmeans.predict()
# print('SC指标: ' + str(metrics.silhouette_score(data, label, metric='euclidean')))
label = label.reshape((32, 32))
# print(label)
mask, masked_img = put_mask(img, label)
ttt += 1
plt.subplot(len(pic_list), len(k_list) * 2 + 1, ttt)
plt.axis('off')
plt.imshow(mask)
if i == 0:
plt.title('K-means', fontdict={'fontsize': 10})
fcm = FCM(k=k_list[kk])
fcm.fit(data)
label = fcm.predict()
label = label.reshape((32, 32))
mask, masked_img = put_mask(img, label)
ttt += 1
plt.subplot(len(pic_list), len(k_list) * 2 + 1, ttt)
plt.axis('off')
plt.imshow(mask)
if i == 0:
plt.title('FCM', fontdict={'fontsize': 10})
# ttt += 1
# plt.subplot(len(pic_list), len(k_list) * 2 + 1, ttt)
# plt.axis('off')
# plt.imshow(masked_img)
plt.show()
.