一、huber函数的近似函数

众所周知我们rmse会对异常值的损失关注度特别高，mae对异常会没有那么敏感。将两者进行结合就可以更加关注大部分的样本的损失，减少关注异常值，在一定程度上提升模型的泛化能力。
$huber_loss = \left\{\begin{matrix} \frac{1}{2}(y_{true} - y_{pred})^2 \ \ \ \ \ \ \ \ \ if\ \ |y_{true} - y_{pred}| < \delta \\ \delta|y_{true} - y_{pred}|-\frac{1}{2}\delta^2 \ \ if\ \ |y_{true} - y_{pred}| >= \delta \end{matrix}\right.$

但是在gbdt模型中，需要运用一阶导与二阶导的比值来结算树节点的拆分增益。mse不具有二阶导。所以我们需要寻找近似可导函数来替代。
$Pseudo\_huber\_loss= \delta ^2(\sqrt{1 + (\frac{\hat{y} - y}{\delta})^2} + 1)$
一阶导：
$\delta ^2\frac{x}{\sqrt{1 + (\frac{x}{\delta})^2}};\ \ x=\hat{y} - y$
二阶导：
$\delta ^2\frac{1}{(1 + (\frac{x}{\delta})^2)^{\frac{3}{2}}}$

二、boston数据集实战

2.1 数据加载

import lightgbm as lgb
from sklearn.datasets import load_boston
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np

bst_dt = load_boston()
bst_df = pd.DataFrame(bst_dt.data, columns = bst_dt.feature_names)
bst_df['target'] = bst_dt.target
x_tr, x_te, y_tr, y_te = train_test_split(bst_df.drop('target', axis=1), bst_df['target'], test_size=0.2, random_state=42)

2.2 sklearn接口lgb简单拟合


lgb_params = {
    'objective' : 'regression',
    'num_leaves' : 30,
    'max_depth': 6,
    'metric': 'rmse',
    'bagging_fraction':0.9,
    'feature_fraction': 0.8,
    'n_jobs': -1 ,
    'n_estimators': 100,
    'subsample_for_bin': 500
}

lgb_model = lgb.LGBMRegressor(**lgb_params)
lgb_model.fit(x_tr, y_tr, eval_set=[(x_tr, y_tr)], verbose=10)
y_pred = lgb_model.predict(x_te)
mae_o = mean_absolute_error(y_te, y_pred)

自定义huber loss

def huber_objective(y_true, y_pred):
    error = y_pred - y_true
    delta = 8
    scale = 1 + (error / delta) ** 2
    scale_sqrt = np.sqrt(scale)
    g = delta * delta / scale * error
    h = delta * delta / scale / scale_sqrt
    return g, h


lgb_params.update({'objective': huber_objective})
print(lgb_params)
lgb_model = lgb.LGBMRegressor(**lgb_params)
lgb_model.fit(x_tr, y_tr, eval_set=[(x_tr, y_tr)], verbose=10)
y_pred = lgb_model.predict(x_te)
mae_huber = mean_absolute_error(y_te, y_pred)
mae_o, mae_huber

结果简单分析

仅仅从rmse上看，很显然，huber loss的损失会更大。我们进一步观察一下拟合差值
的分布情况。

"""
- rmse
[10]    training's rmse: 4.78619
[20]    training's rmse: 3.35349
[30]    training's rmse: 2.84163
[40]    training's rmse: 2.56263
[50]    training's rmse: 2.35089
[60]    training's rmse: 2.20306
[70]    training's rmse: 2.06908
[80]    training's rmse: 1.95886
[90]    training's rmse: 1.86569
[100]   training's rmse: 1.79135
- huber
[10]    training's rmse: 5.49376
[20]    training's rmse: 3.54926
[30]    training's rmse: 3.07389
[40]    training's rmse: 2.89136
[50]    training's rmse: 2.73511
[60]    training's rmse: 2.61101
[70]    training's rmse: 2.50242
[80]    training's rmse: 2.42138
[90]    training's rmse: 2.35478
[100]   training's rmse: 2.30335
(2.116972786370626, 2.0635595381991485)

"""

从差值中，我们可以看出huber loss 对较为集中的值拟合较好，会忽略部分异常值。从target的分布看确实存在着小部分的异常值。用huber loss拟合的模型会具有更佳的泛化能力。
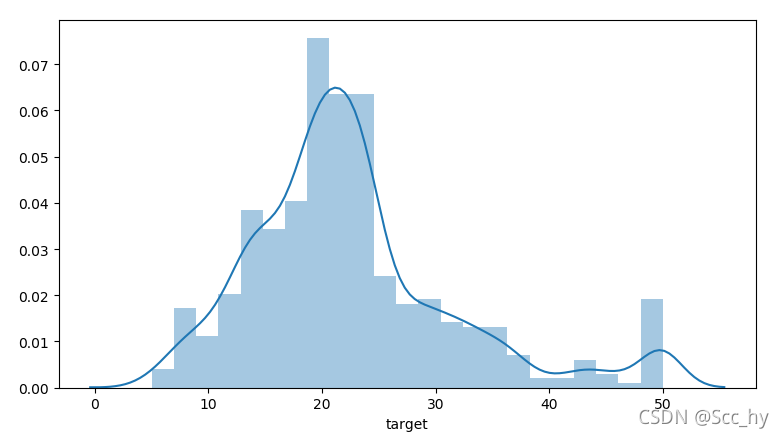
在这里插入图片描述

import matplotlib.pyplot as plt
import seaborn as sns
sns.distplot(bst_df['target'])
plt.show()

"""
rmse loss
>>> (y_te-y_pred).map(int).value_counts()
 0     33
 1     16
-1     16
 2     11
-2      9
 4      5
 3      3
-3      3
-6      1
-5      1
 18     1
-12     1
 7      1
 5      1
# huber loss
>>> (y_te-y_pred).map(int).value_counts()
 0     37
-1     18
 1     10
-2      9
 2      8
 3      7
-3      4
-5      2
 4      2
 23     1
-10     1
 7      1
 6      1
 5      1
"""