注意，我们用神经网络代替模型，用学习规则代替机器学习。
Nodes of a Neural Network
①在神经网络的上下文中，确定模型（神经网络）的过程称为学习规则。
②计算机将信息存储在存储器的特定位置
③由于大脑由许多神经元的连接组成，因此神经网络由节点的连接构成，节点是与大脑神经元相对应的元素。
④神经网络使用权值模拟神经元的关联
神经网络的信息以权重和偏差的形式存储（b是偏差）
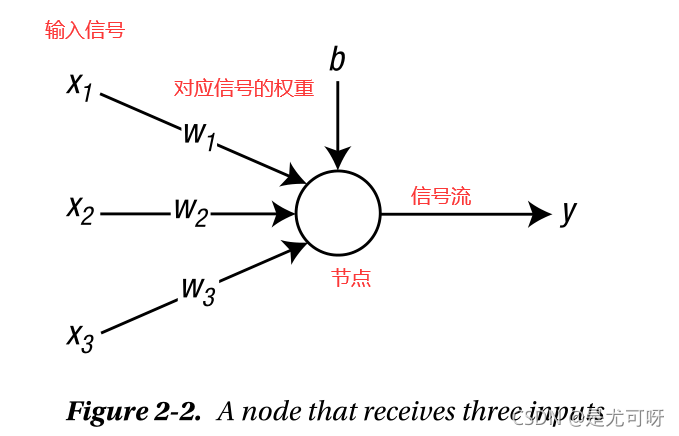
来自外部的输入信号在到达节点之前乘以权重。一旦在节点上收集了加权信号，这些值就被添加为加权和。
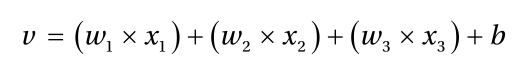该方程表明，权重越大的信号影响越大。
（矩阵就是行列式，用行×列）
Layers of Neural Network
因为大脑是一个巨大的神经元网络，所以神经网络是一个节点网络。根据节点的连接方式，可以创建各种神经网络。一种最常用的神经网络类型采用了节点分层结构，
①输入层的节点仅充当将输入信号传输到下一个节点的通道。因此，它们不计算加权和和激活函数。
②相反，最右边的节点组称为输出层。这些节点的输出成为神经网络的最终结果。
③输入层和输出层之间的层称为隐藏层。它们之所以被命名是因为它们无法从神经网络外部访问。
- 只有输入层和输出层，称为单层神经网络
- 将隐藏层添加到单层神经网络时，将生成多层神经网络。多层神经网络由输入层、隐藏层和输出层组成。
- 具有单个隐藏层的神经网络称为浅层神经网络或普通神经网络。包含两个或更多隐藏层的多层神经网络称为深层神经网络。
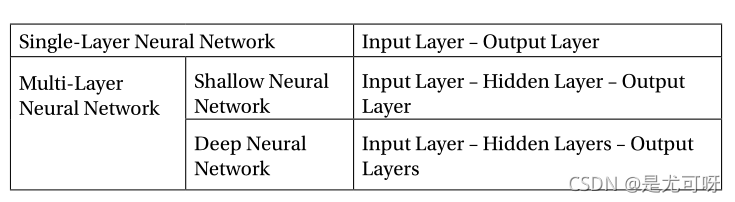
神经网络的分支取决于层结构
一层上的节点同时接收信号，同时将处理后的信号发送到下一层。
（是算单层神经网络的隐藏层而不是输入层的原因：输入层不需要计算，只负责传送）
（权重的书写方法）
对节点使用线性函数会抵消添加层的效果。
多层隐藏层变成一层
在实际应用中，线性函数 不能作为隐含层的激活函数。这是因为线性函数抵消了隐藏层的影响。
但在回归等问题中，输出层节点可以采用线性函数。
Supervised Learning of a Neural Network
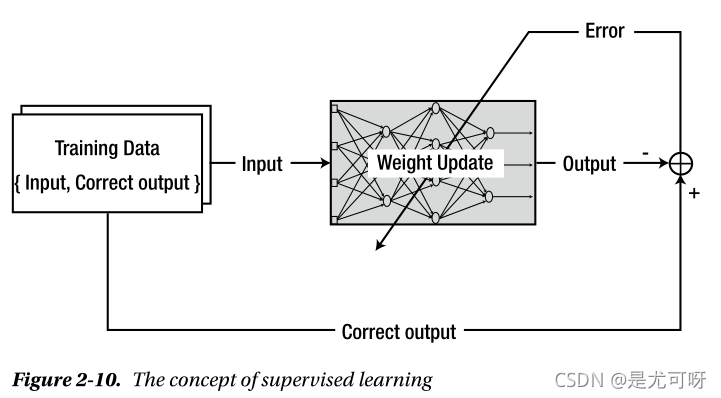
Training of a Single-Layer Neural Network: Delta Rule
如前所述，神经网络以权值的形式存储信息。根据给定信息修改权重的系统方法称为学习规则。由于训练是神经网络系统存储信息的唯一途径，学习规则是神经网络研究的重要组成部分。
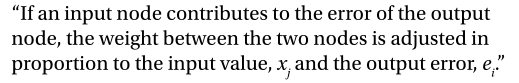（如果输入节点导致输出节点的误差，则两个节点之间的权重将按照输入值xj和输出误差ei的比例进行调整）
学习率α决定了每次权重变化的程度。
如果该值太高，则输出会在解决方案周围徘徊，无法收敛。
相反，如果值太低，则计算速度太慢。
唯一的区别是增加了步骤6。步骤6只是说明整个培训过程是重复的。
一旦完成步骤5，就可以使用每个数据点对模型进行训练。
那么，为什么我们要使用所有相同的训练数据来训练它呢？这是因为增量规则在重复过程时搜索解决方案，而不是一次解决所有问题。3整个过程都在重复，因为使用相同的数据重新训练模型可能会改进模型。
所有训练数据都经过步骤2-5一次的训练迭代次数称为epoch。例如，epoch=10意味着神经网络使用相同的数据集经历10个重复的训练过程。
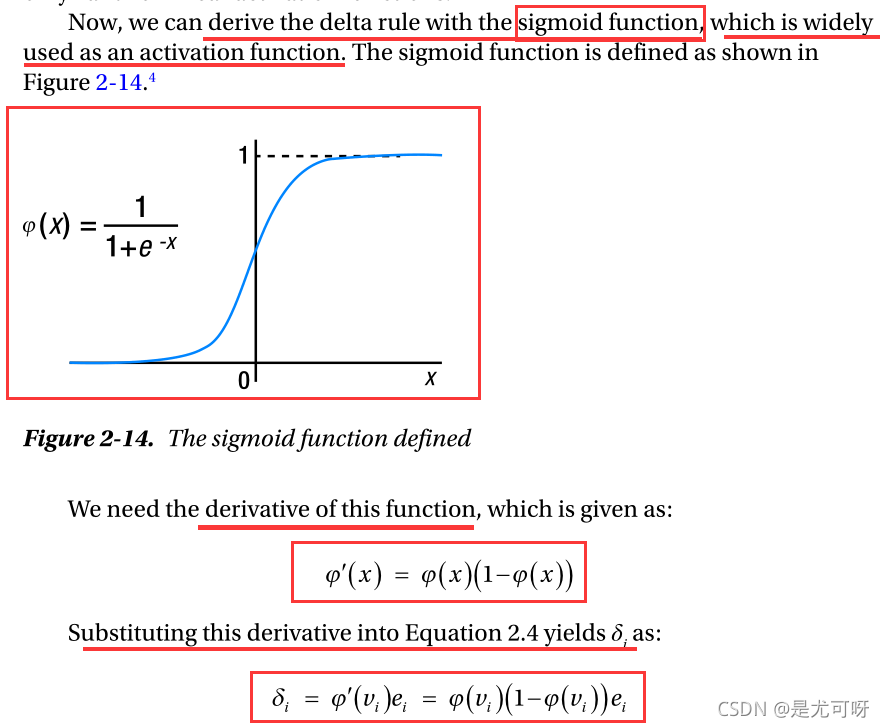
Generalized Delta Rule
SGD, Batch, and Mini Batch
计算权重更新（?wij）的方法
Stochastic Gradient Descent
计算每个训练数据的误差，并立即调整权重。
如果我们有100个训练数据点，SGD会调整权重100次。
当SGD调整每个数据点的权重时，神经网络的性能在训练过程中会发生扭曲。“随机”这个名称意味着训练过程的随机行为。SGD计算重量更新为：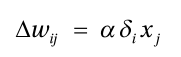
（delta原则基于这个方法）
Batch
在批处理方法中，针对训练数据的所有错误计算每个权重更新，并使用权重更新的平均值来调整权重。此方法使用所有训练数据，只更新一次。图2-16说明了批量法的重量更新计算和训练过程。
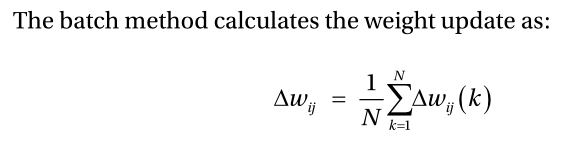
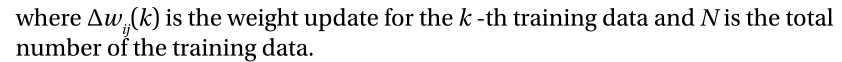由于平均权重更新计算，批处理方法需要大量的训练时间。
Mini Batch☆
小批量法是SGD法和批量法的混合。它选择训练数据集的一部分，并在批处理方法中将其用于训练。因此，它计算选定数据的权重更新，并使用平均权重更新训练神经网络。
当选择适当数量的数据点时，小批量方法可以从两种方法中获得好处：SGD的速度和批量的稳定性。由于这个原因，它经常被用于深度学习，这需要处理大量的数据。
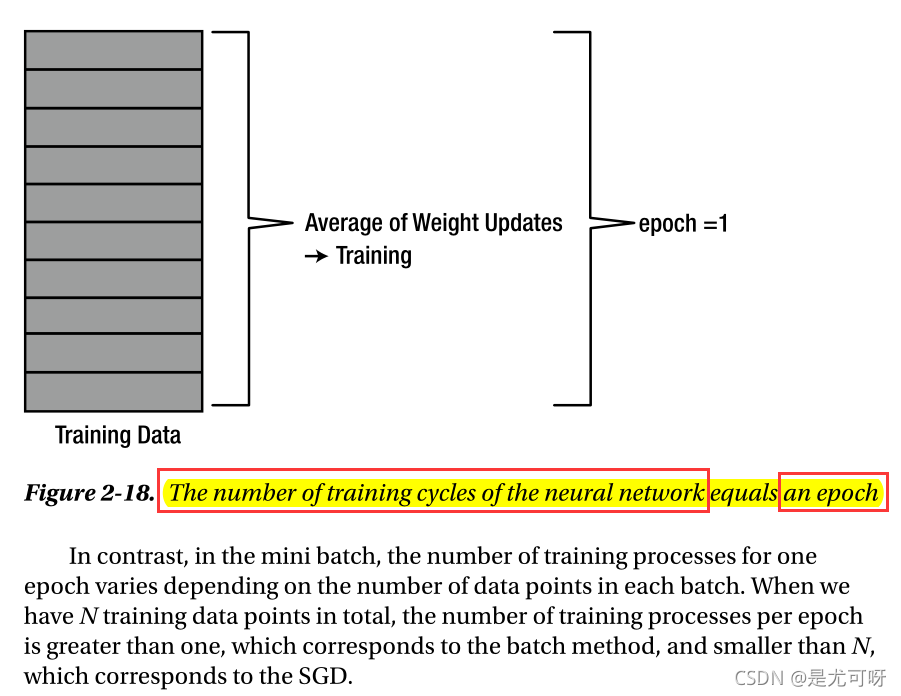
在小批量中，一个历元的训练过程数量取决于每个批次中的数据点数量。当我们总共有N个训练数据点时，每个历元的训练进程数大于1（对应于批处理方法），小于N（对应于SGD）。
单层和多层的区别：
单层神经网络解决：linearly separable problem（线性可分问题）这是因为单层神经网络是一个线性划分输入数据空间的模型。
多层神经网络解决： linearly inseparable problem（线性不可分问题）
单层神经网络是适用于特定的问题类型。多层神经网络没有这样的限制。