首先,以输入特征数为2,样本数为1,层数为2的神经网络举例子(隐藏层1层+输出层1层)
激活函数为sigmoid函数
所以有以下的网络

一般输入层不算入层数,在这里写为第0层。
第0层有两个输入特征,1个样本数,所以矩阵维度为[2,1]
第1层有4个单元数,所以矩阵维度的第一维为4,第二维为前一层的单元数(即第0层),所以第1层的矩阵维度为[4,2]
第2层有1个单元数,所以矩阵维度的第一维为1,第二维为前一层的单元数(即第1层),所以第2层的矩阵维度为[1,4]
一般一个单元里面有两个计算,一个是线性计算,一个的激活函数
线性计算为 z = W * x + b
激活函数为 a = σ(z)
如果把这两条式子代入神经网络中,
首先把特征数输入第0层,假设有2个特征,1个样本,那么x的维度就是[2,1]
而 W为第一层的参数,所以维度为[4,2]
z[ __, __ ]=W[4,2] * x [2,1] + b[ __ , __]
由矩阵运算可知z的维度应为[4,1],所以b的维度也为[4,1]
即z[4, 1 ]=W[4,2] * x [2,1] + b[4,1]
接着经过激活函数a = σ(z),所以a的维度也为[4,1]
接着来到第二层,第一层的输出为a,a则作为第二层的输入,所以有:
z = W * a + b
z[ __, __ ]=W[__,__] * a [4,1] + b[ __ , __]
而第二层的参数W的维度为[1,4],所以:
z[ __, __ ]=W[1,4] * a [4,1] + b[ __ , __]
同理可得z的维度和b的维度
z[ 1, 1]=W[1,4] * a [4,1] + b[1,1]
接着,接着经过激活函数y= σ(z),输出y
那么,可以推广到m个样本
首先把样本输入第0层,假设有2个特征,m个样本,那么x的维度就是[2,m]
而 W为第一层的参数,所以维度为[4,2]
z[ __, __ ]=W[4,2] * x [2,m] + b[ __ , __]
由矩阵运算可知z的维度应为[4,m],所以b的维度也为[4,m]
即z[4, m ]=W[4,2] * x [2,m] + b[4,m]
接着经过激活函数a = σ(z),所以a的维度也为[4,m]
接着来到第二层,第一层的输出为a,a则作为第二层的输入,所以有:
z = W * a + b
z[ __, __ ]=W[__,__] * a [4,m] + b[ __ , __]
而第二层的参数W的维度为[1,4],所以:
z[ __, __ ]=W[1,4] * a [4,m] + b[ __ , __]
同理可得z的维度和b的维度
z[ 1, m]=W[1,4] * a [4,m] + b[1,m]
上面为2层神经网络,接着推广到多层网络:
假设n^L 代表第L层的单元数
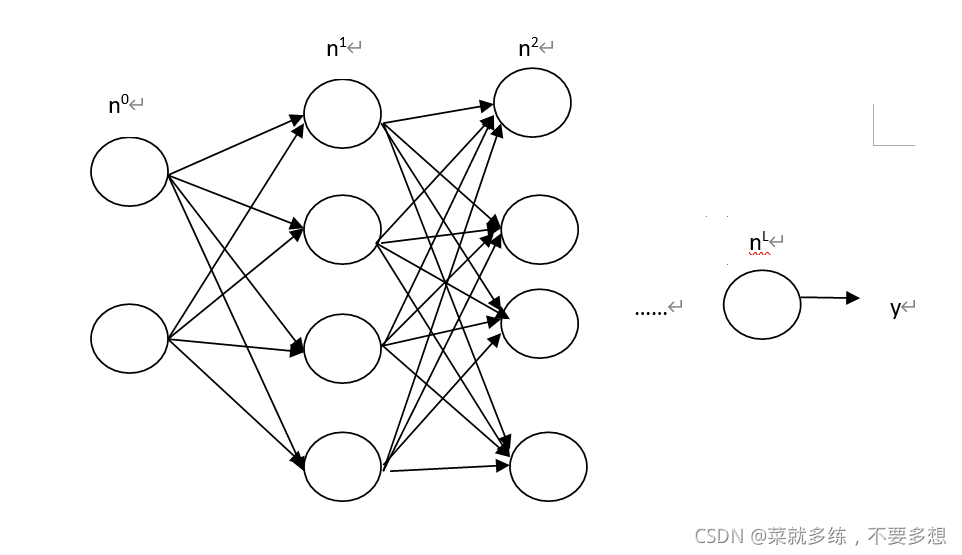
那么第L(0层除外)层的w矩阵维度为[n^L ,n^(L-1)]
而第L(0层除外)层的b矩阵维度为[n^L ,m]
m代表样本数