数据统计与分析实验四:机器学习算法建模与求解(R语言)
1、对于下表中的数据,对1990年-2006年内的数据建立人口自然增长率对于国民总收入、CPI增长率和人均GDP的三元线性回归模型。
1.1 手动输入数据到csv文件
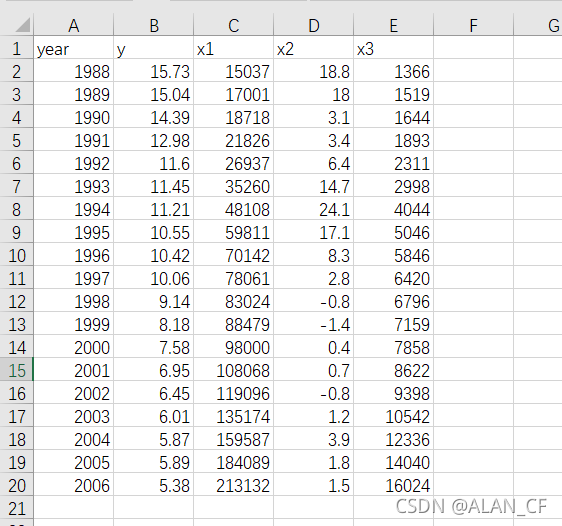
1.2 导入数据、检查数据、建立多元线性回归统计模型
> Data<-read.csv("E:\\CODING__ALAN_CF\\R_programLanguage\\data_4-1.csv")#从csv文件导入数据
> Data #检查数据
year y x1 x2 x3
1 1988 15.73 15037 18.8 1366
2 1989 15.04 17001 18.0 1519
3 1990 14.39 18718 3.1 1644
4 1991 12.98 21826 3.4 1893
5 1992 11.60 26937 6.4 2311
6 1993 11.45 35260 14.7 2998
7 1994 11.21 48108 24.1 4044
8 1995 10.55 59811 17.1 5046
9 1996 10.42 70142 8.3 5846
10 1997 10.06 78061 2.8 6420
11 1998 9.14 83024 -0.8 6796
12 1999 8.18 88479 -1.4 7159
13 2000 7.58 98000 0.4 7858
14 2001 6.95 108068 0.7 8622
15 2002 6.45 119096 -0.8 9398
16 2003 6.01 135174 1.2 10542
17 2004 5.87 159587 3.9 12336
18 2005 5.89 184089 1.8 14040
19 2006 5.38 213132 1.5 16024
> Data$year
[1] 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005
[19] 2006
> Data$y
[1] 15.73 15.04 14.39 12.98 11.60 11.45 11.21 10.55 10.42 10.06 9.14 8.18 7.58 6.95 6.45
[16] 6.01 5.87 5.89 5.38
> Data$x1
[1] 15037 17001 18718 21826 26937 35260 48108 59811 70142 78061 83024 88479 98000
[14] 108068 119096 135174 159587 184089 213132
> Data$x2
[1] 18.8 18.0 3.1 3.4 6.4 14.7 24.1 17.1 8.3 2.8 -0.8 -1.4 0.4 0.7 -0.8 1.2 3.9 1.8
[19] 1.5
> Data$x3
[1] 1366 1519 1644 1893 2311 2998 4044 5046 5846 6420 6796 7159 7858 8622 9398
[16] 10542 12336 14040 16024
> str(Data)#查看数据的结构
'data.frame': 19 obs. of 5 variables:
$ year: int 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 ...
$ y : num 15.7 15 14.4 13 11.6 ...
$ x1 : int 15037 17001 18718 21826 26937 35260 48108 59811 70142 78061 ...
$ x2 : num 18.8 18 3.1 3.4 6.4 14.7 24.1 17.1 8.3 2.8 ...
$ x3 : int 1366 1519 1644 1893 2311 2998 4044 5046 5846 6420 ...
> summary(Data)#查看数据统计信息
year y x1 x2 x3
Min. :1988 Min. : 5.380 Min. : 15037 Min. :-1.400 Min. : 1366
1st Qu.:1992 1st Qu.: 6.700 1st Qu.: 31099 1st Qu.: 0.950 1st Qu.: 2654
Median :1997 Median :10.060 Median : 78061 Median : 3.100 Median : 6420
Mean :1997 Mean : 9.731 Mean : 83134 Mean : 6.484 Mean : 6624
3rd Qu.:2002 3rd Qu.:11.525 3rd Qu.:113582 3rd Qu.:11.500 3rd Qu.: 9010
Max. :2006 Max. :15.730 Max. :213132 Max. :24.100 Max. :16024
>
> lm1<-lm(y~x1+x2+x3,data = Data) #建立多元线性回归模型
> lm1 #打印参数估计的结果
Call:
lm(formula = y ~ x1 + x2 + x3, data = Data)
Coefficients:
(Intercept) x1 x2 x3
15.7197750 0.0003751 0.0497390 -0.0056601
>
也就是:y=0.0003751 * x1 + 0.0497390 * x2 + (-0.0056601) * x3 + 15.7197750
1.3 显著性检验
#显著性检验
> summary(lm1)
Call:
lm(formula = y ~ x1 + x2 + x3, data = Data)
Residuals:
Min 1Q Median 3Q Max
-1.4613 -0.6229 -0.0797 0.7153 1.2592
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.7197750 0.8702058 18.064 1.37e-11 ***
x1 0.0003751 0.0001061 3.535 0.00300 **
x2 0.0497390 0.0329629 1.509 0.15209
x3 -0.0056601 0.0014259 -3.969 0.00123 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9091 on 15 degrees of freedom
Multiple R-squared: 0.9363, Adjusted R-squared: 0.9236
F-statistic: 73.5 on 3 and 15 DF, p-value: 3.379e-09
>
其中
Estimate Std. Error t value Pr(>|t|)
估值,标准误差,T值,P值
P值小于0.05的变量,在统计意义上对因变量y的线性回归具有显著意义
所以,截距项(Intercept)和x1,x3通过显著性检验
Multiple R-squared和Adjusted R-squared这两个值,常称之为“拟合优度”和“修正的拟合优度”,是指回归方程对样本的拟合程度几何,这里我们可以看到,修正的拟合优度=0.9263,也就是大概拟合程度大概九成多一点,这个值当然是越高越好
F-statistic,也就是常说的F检验,常常用于判断方程整体的显著性检验,其P值为3.379e-09,显然是<0.05的,我们可以认为方程在P=0.05的水平上还是通过显著性检验的。
总结:
T检验是检验解释变量的显著性的;
R-squared是查看方程拟合程度的;
F检验是检验方程整体显著性的;
1.4 残差分析(我不是特别理解含义)
> par(mfrow=c(2,2))#一页多图,一页四图(不重叠)
> plot(lm1)
>
> #关于残差的分析图
> #残差和拟合值(左上)
> #残差QQ图(右上)
> #标准化残差平方根和拟合值(左下)
> #标准化残差和杠杆值(右下)
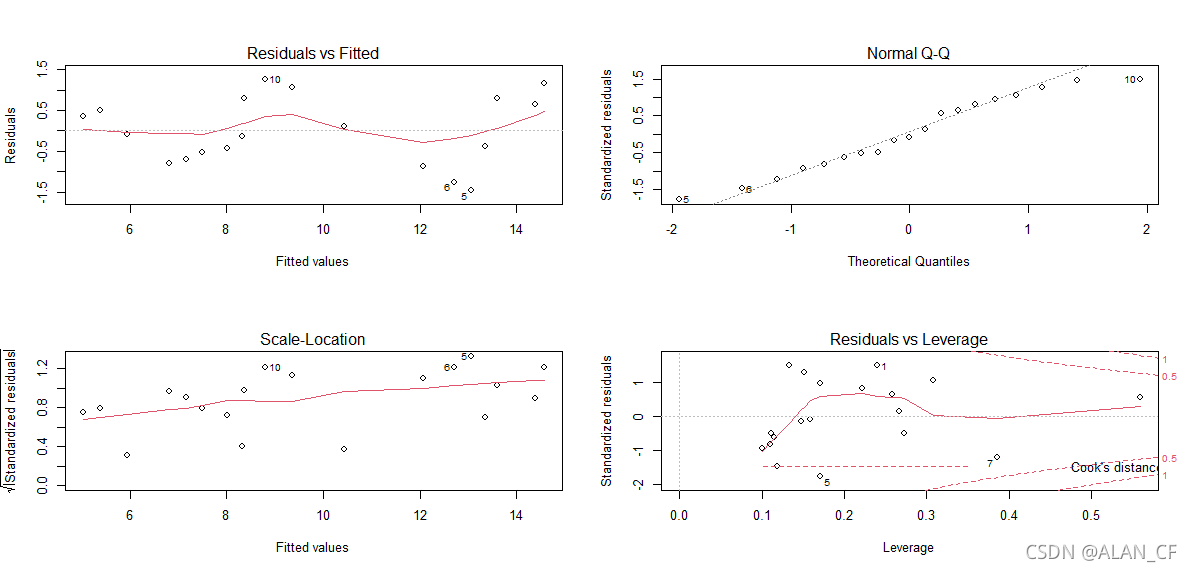
1.5 拿1988-2006的模型预测2020,发现与实际的2020的人口自然增长率不符(毕竟数据老了很多)
以2020年,人均GDP72447元,CPI上涨2.5%,国民总收入1009151亿元,人口自然增长率0.145% x1=1009151,x2=2.5,x3=72447
> newdata<-data.frame(year=2020,x1=1009151,x2=2.5,x3=72447)
> predict<-predict(lm1,newdata = newdata,interval = "predict")
> predict
fit lwr upr
1 -15.69411 -28.39739 -2.990832
所以用1988-2006年的模型预测2020年并不准确
2、下载UCI中wine数据集:http://archive.ics.uci.edu/ml/datasets/Wine。所下载数据可以用txt打开,其中每一行数据为一种Wine的记录,每条记录包含14个维度,其中第一维为该Wine类别,后面13维为具体的Wine属性。请基于所有的178个Wine样本对Wine的13个维度进行PCA降维分析,将贡献率之和大于90%的成分提取,并将原13维属性数据映射为新数据。
主成分分析直接调用函数就行,但是13个属性的累计贡献率之和怎么都在90%以上啊??!!!,后面怎么做?不晓得~
> wine<-read.table(file = "C:\\Users\\15328\\Desktop\\数据统计与分析基础\\wine.data",
+ header = FALSE,
+ sep=',')
> wine
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14
1 1 14.23 1.71 2.43 15.6 127 2.80 3.06 0.28 2.29 5.64 1.040 3.92 1065
2 1 13.20 1.78 2.14 11.2 100 2.65 2.76 0.26 1.28 4.38 1.050 3.40 1050
3 1 13.16 2.36 2.67 18.6 101 2.80 3.24 0.30 2.81 5.68 1.030 3.17 1185
4 1 14.37 1.95 2.50 16.8 113 3.85 3.49 0.24 2.18 7.80 0.860 3.45 1480
5 1 13.24 2.59 2.87 21.0 118 2.80 2.69 0.39 1.82 4.32 1.040 2.93 735
6 1 14.20 1.76 2.45 15.2 112 3.27 3.39 0.34 1.97 6.75 1.050 2.85 1450
7 1 14.39 1.87 2.45 14.6 96 2.50 2.52 0.30 1.98 5.25 1.020 3.58 1290
8 1 14.06 2.15 2.61 17.6 121 2.60 2.51 0.31 1.25 5.05 1.060 3.58 1295
9 1 14.83 1.64 2.17 14.0 97 2.80 2.98 0.29 1.98 5.20 1.080 2.85 1045
10 1 13.86 1.35 2.27 16.0 98 2.98 3.15 0.22 1.85 7.22 1.010 3.55 1045
11 1 14.10 2.16 2.30 18.0 105 2.95 3.32 0.22 2.38 5.75 1.250 3.17 1510
12 1 14.12 1.48 2.32 16.8 95 2.20 2.43 0.26 1.57 5.00 1.170 2.82 1280
13 1 13.75 1.73 2.41 16.0 89 2.60 2.76 0.29 1.81 5.60 1.150 2.90 1320
14 1 14.75 1.73 2.39 11.4 91 3.10 3.69 0.43 2.81 5.40 1.250 2.73 1150
15 1 14.38 1.87 2.38 12.0 102 3.30 3.64 0.29 2.96 7.50 1.200 3.00 1547
16 1 13.63 1.81 2.70 17.2 112 2.85 2.91 0.30 1.46 7.30 1.280 2.88 1310
17 1 14.30 1.92 2.72 20.0 120 2.80 3.14 0.33 1.97 6.20 1.070 2.65 1280
18 1 13.83 1.57 2.62 20.0 115 2.95 3.40 0.40 1.72 6.60 1.130 2.57 1130
19 1 14.19 1.59 2.48 16.5 108 3.30 3.93 0.32 1.86 8.70 1.230 2.82 1680
20 1 13.64 3.10 2.56 15.2 116 2.70 3.03 0.17 1.66 5.10 0.960 3.36 845
21 1 14.06 1.63 2.28 16.0 126 3.00 3.17 0.24 2.10 5.65 1.090 3.71 780
22 1 12.93 3.80 2.65 18.6 102 2.41 2.41 0.25 1.98 4.50 1.030 3.52 770
23 1 13.71 1.86 2.36 16.6 101 2.61 2.88 0.27 1.69 3.80 1.110 4.00 1035
24 1 12.85 1.60 2.52 17.8 95 2.48 2.37 0.26 1.46 3.93 1.090 3.63 1015
25 1 13.50 1.81 2.61 20.0 96 2.53 2.61 0.28 1.66 3.52 1.120 3.82 845
26 1 13.05 2.05 3.22 25.0 124 2.63 2.68 0.47 1.92 3.58 1.130 3.20 830
27 1 13.39 1.77 2.62 16.1 93 2.85 2.94 0.34 1.45 4.80 0.920 3.22 1195
28 1 13.30 1.72 2.14 17.0 94 2.40 2.19 0.27 1.35 3.95 1.020 2.77 1285
29 1 13.87 1.90 2.80 19.4 107 2.95 2.97 0.37 1.76 4.50 1.250 3.40 915
30 1 14.02 1.68 2.21 16.0 96 2.65 2.33 0.26 1.98 4.70 1.040 3.59 1035
31 1 13.73 1.50 2.70 22.5 101 3.00 3.25 0.29 2.38 5.70 1.190 2.71 1285
32 1 13.58 1.66 2.36 19.1 106 2.86 3.19 0.22 1.95 6.90 1.090 2.88 1515
33 1 13.68 1.83 2.36 17.2 104 2.42 2.69 0.42 1.97 3.84 1.230 2.87 990
34 1 13.76 1.53 2.70 19.5 132 2.95 2.74 0.50 1.35 5.40 1.250 3.00 1235
35 1 13.51 1.80 2.65 19.0 110 2.35 2.53 0.29 1.54 4.20 1.100 2.87 1095
36 1 13.48 1.81 2.41 20.5 100 2.70 2.98 0.26 1.86 5.10 1.040 3.47 920
37 1 13.28 1.64 2.84 15.5 110 2.60 2.68 0.34 1.36 4.60 1.090 2.78 880
38 1 13.05 1.65 2.55 18.0 98 2.45 2.43 0.29 1.44 4.25 1.120 2.51 1105
39 1 13.07 1.50 2.10 15.5 98 2.40 2.64 0.28 1.37 3.70 1.180 2.69 1020
40 1 14.22 3.99 2.51 13.2 128 3.00 3.04 0.20 2.08 5.10 0.890 3.53 760
41 1 13.56 1.71 2.31 16.2 117 3.15 3.29 0.34 2.34 6.13 0.950 3.38 795
42 1 13.41 3.84 2.12 18.8 90 2.45 2.68 0.27 1.48 4.28 0.910 3.00 1035
43 1 13.88 1.89 2.59 15.0 101 3.25 3.56 0.17 1.70 5.43 0.880 3.56 1095
44 1 13.24 3.98 2.29 17.5 103 2.64 2.63 0.32 1.66 4.36 0.820 3.00 680
45 1 13.05 1.77 2.10 17.0 107 3.00 3.00 0.28 2.03 5.04 0.880 3.35 885
46 1 14.21 4.04 2.44 18.9 111 2.85 2.65 0.30 1.25 5.24 0.870 3.33 1080
47 1 14.38 3.59 2.28 16.0 102 3.25 3.17 0.27 2.19 4.90 1.040 3.44 1065
48 1 13.90 1.68 2.12 16.0 101 3.10 3.39 0.21 2.14 6.10 0.910 3.33 985
49 1 14.10 2.02 2.40 18.8 103 2.75 2.92 0.32 2.38 6.20 1.070 2.75 1060
50 1 13.94 1.73 2.27 17.4 108 2.88 3.54 0.32 2.08 8.90 1.120 3.10 1260
51 1 13.05 1.73 2.04 12.4 92 2.72 3.27 0.17 2.91 7.20 1.120 2.91 1150
52 1 13.83 1.65 2.60 17.2 94 2.45 2.99 0.22 2.29 5.60 1.240 3.37 1265
53 1 13.82 1.75 2.42 14.0 111 3.88 3.74 0.32 1.87 7.05 1.010 3.26 1190
54 1 13.77 1.90 2.68 17.1 115 3.00 2.79 0.39 1.68 6.30 1.130 2.93 1375
55 1 13.74 1.67 2.25 16.4 118 2.60 2.90 0.21 1.62 5.85 0.920 3.20 1060
56 1 13.56 1.73 2.46 20.5 116 2.96 2.78 0.20 2.45 6.25 0.980 3.03 1120
57 1 14.22 1.70 2.30 16.3 118 3.20 3.00 0.26 2.03 6.38 0.940 3.31 970
58 1 13.29 1.97 2.68 16.8 102 3.00 3.23 0.31 1.66 6.00 1.070 2.84 1270
59 1 13.72 1.43 2.50 16.7 108 3.40 3.67 0.19 2.04 6.80 0.890 2.87 1285
60 2 12.37 0.94 1.36 10.6 88 1.98 0.57 0.28 0.42 1.95 1.050 1.82 520
61 2 12.33 1.10 2.28 16.0 101 2.05 1.09 0.63 0.41 3.27 1.250 1.67 680
62 2 12.64 1.36 2.02 16.8 100 2.02 1.41 0.53 0.62 5.75 0.980 1.59 450
63 2 13.67 1.25 1.92 18.0 94 2.10 1.79 0.32 0.73 3.80 1.230 2.46 630
64 2 12.37 1.13 2.16 19.0 87 3.50 3.10 0.19 1.87 4.45 1.220 2.87 420
65 2 12.17 1.45 2.53 19.0 104 1.89 1.75 0.45 1.03 2.95 1.450 2.23 355
66 2 12.37 1.21 2.56 18.1 98 2.42 2.65 0.37 2.08 4.60 1.190 2.30 678
67 2 13.11 1.01 1.70 15.0 78 2.98 3.18 0.26 2.28 5.30 1.120 3.18 502
68 2 12.37 1.17 1.92 19.6 78 2.11 2.00 0.27 1.04 4.68 1.120 3.48 510
69 2 13.34 0.94 2.36 17.0 110 2.53 1.30 0.55 0.42 3.17 1.020 1.93 750
70 2 12.21 1.19 1.75 16.8 151 1.85 1.28 0.14 2.50 2.85 1.280 3.07 718
71 2 12.29 1.61 2.21 20.4 103 1.10 1.02 0.37 1.46 3.05 0.906 1.82 870
[ reached 'max' / getOption("max.print") -- omitted 107 rows ]
#到达最大显示幅度可能?后面还有107行没有显示出来
> pc_wine<-princomp(wine[,2:14])#主成分分析
> pc_wine
Call:
princomp(x = wine[, 2:14])
Standard deviations:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 Comp.9 Comp.10 Comp.11
314.07718175 13.09831925 3.06350952 2.22781020 1.10541467 0.91451560 0.52669370 0.38798300 0.33386675 0.26702019 0.19329997
Comp.12 Comp.13
0.14475490 0.09031952
13 variables and 178 observations.
> summary(pc_wine)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 Comp.9
Standard deviation 314.0771817 13.098319252 3.063510e+00 2.227810e+00 1.105415e+00 9.145156e-01 5.266937e-01 3.879830e-01 3.338668e-01
Proportion of Variance 0.9980912 0.001735916 9.495896e-05 5.021736e-05 1.236368e-05 8.462130e-06 2.806815e-06 1.523081e-06 1.127830e-06
Cumulative Proportion 0.9980912 0.999827146 9.999221e-01 9.999723e-01 9.999847e-01 9.999931e-01 9.999960e-01 9.999975e-01 9.999986e-01
Comp.10 Comp.11 Comp.12 Comp.13
Standard deviation 2.670202e-01 1.933000e-01 1.447549e-01 9.031952e-02
Proportion of Variance 7.214158e-07 3.780603e-07 2.120138e-07 8.253928e-08
Cumulative Proportion 9.999993e-01 9.999997e-01 9.999999e-01 1.000000e+00
>
# 第一行是特征值(Standard deviation),
# 第二列是方差的贡献率(Proportion of Variance)
# 第三列是累计方差的贡献率(Cumulative Proportion)
# 方差的贡献率: 标准化后的特征值,全部相加等于100%
# 累计方差的贡献率:累加后的方差的贡献率
