VC Dimension
机器学习必须满足两个重要的条件,才能够学到有用的东西:
- 假设空间H的size M有限,当N足够大的时候,挑选一个g,使得 E i n ( g ) ≈ E o u t ( g ) E_{in}(g)\approx E_{out}(g) Ein?(g)≈Eout?(g)
- 利用某种演算法A,在M中挑选一个g使得 E i n ( g ) ≈ E_{in}(g)\approx Ein?(g)≈ 0
以上两个过程对应了机器学习的训练和测试,训练时所做的事情是让 E i n ( g ) ≈ E_{in}(g)\approx Ein?(g)≈ 0 。测试则是希望 E o u t ( g ) E_{out}(g) Eout?(g)尽可能的接近 E i n ( g ) E_{in}(g) Ein?(g)。
基于这个原因,我们引入了break point,只要break point存在,我们就能推出,M的增长函数是多项式级别的。在根据上界函数的相关内容,就能很容易得出 E i n ( g ) ≈ E o u t ( g ) E_{in}(g)\approx E_{out}(g) Ein?(g)≈Eout?(g)
这次引入一个新的概念,VC Dimension。
1.定义
在定义VC dimension之前,需要先了解几个概念。
如果一个假设空间H 有break point k,那么它的成长函数是有界的,它的上界称为Bound function。由数学归纳法知,Bound function也是有界的,且上界为
N
K
?
1
N^{K-1}
NK?1。还有一个内容是关于VC bound的。VC bound的推导过程较为复杂,只需要了解一下他的内容就行。大体内容和霍夫定不等式说的事情一样,只不过将霍夫定不等式进行了更加具体的表述:
该不等式的最终结果只和N和k有关。N为样本的数量,不需要太过关注,集中精力来解决k的问题。如果在假设空间
H
H
H中存在k,那么根据VC bound,该模型具有良好的泛化能力,保证了预测结果的可行性。只需要尽可能的让
E
i
n
(
g
)
E_{in}(g)
Ein?(g)接近0就行。
VC dimension:在空间
H
H
H中,能最大完全二分点的数目(shatter),最大的完全正确的分类能力。列如输入N个点,最大的分类情况为
2
N
2^N
2N种,如果存在函数,能够将所有的情况都进行分类,那么N就是该空间的VC dimension。VC dimension的值为break point-1。
可以回想一下之前介绍的四个列子,他们对应的dimension是多少:
用
d
v
c
d_{vc}
dvc?来代替k,VC bound就转化为,N和
d
v
c
d_{vc}
dvc?之间的问题了,如果一个空间的
d
v
c
d_{vc}
dvc?确定,那么机器学习的两个核心问题就解决了一个,能够保证
E
i
n
(
g
)
≈
E_{in}(g)\approx
Ein?(g)≈
E
o
u
t
(
g
)
E_{out}(g)
Eout?(g)与样本分布,目标函数都无关。
2.VC dimension和2DPLA
简单回顾2D PLA算法,已知perceptions的k=4,则 d v c d_{vc} dvc?=3。以下两个条件保证了2维线性可分数据是可以学习的》
- 线性可分数据通过PLA算法运行足够长的时间,一定可以找出一条正确分类的直线,使得样本中没有分错的数据。
- 在训练样本和整个数据集服从同一分布的情况下,有了VC的限制,保证了在 d v c d_{vc} dvc?=3训练样本N足够大时, E i n ( g ) ≈ E_{in}(g)\approx Ein?(g)≈ E o u t ( g ) E_{out}(g) Eout?(g)。
以上两个共同条件得出:如果找到一个g使得 E i n ( g ) ≈ E_{in}(g)\approx Ein?(g)≈ 0,那么就能证明PLA是可以学习的。
如果是多维的PLA,他对应的
d
v
c
d_{vc}
dvc?又是多少呢:1D
d
v
c
d_{vc}
dvc?=2,2D
d
v
c
d_{vc}
dvc?=3。那么我们就假设在n维的情况下,
d
v
c
d_{vc}
dvc?=n+1.经过证明该命题正确。具体证明可以参考林轩田老师的机器学习技法课程的VC dimension一节。
3.直观理解VC dimension
通过上面的分析,我们将感知机的维度和VC联系了起来。也大体了解了dimension的含义。在感知机中数据样本的维度又和权值向量的维度一致。 不同的权重向量对应着不同的假设函数,因此称假设函数的参数是假设空间的自由度。自由度可任意调节。如果从假设空间的数量上去描述,则自由度是无限大的,但是如果从二元感知机分类这一限制条件上去入手 ,可以使用VC来衡量其自由度。VC dimension代表了假设空间的分类能力,反映了H的自由度,也就等于features的个数。
上图中Positive Rays 的列子里,VC dimension
d
v
c
d_{vc}
dvc?=1时,假设空间有1个参数,Positive Intervals 的例子中,VC dimension
d
v
c
d_{vc}
dvc?=1时,假设空间有两个参数,即左右边界点。因此在大部分情况下,VC dimension
d
v
c
d_{vc}
dvc?大致等于假设空间的参数个数。
对于2D perceptions,线性分类
d
v
c
d_{vc}
dvc?=3.从而得到如下结论:
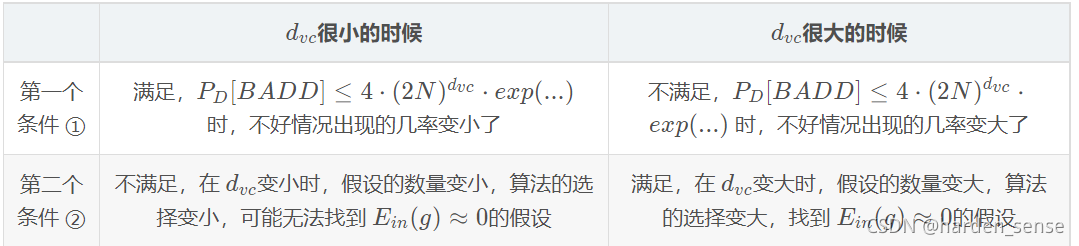
在一些书中,参数较多的模型都称为复杂模型,很少给出解释,这一节的内容给出了很好的解释,因为在很多情况下模型参数的个数大致等于VC维的个数。参数越多或者说模型越复杂,越有可能找出使
E
i
n
E _{i n}
Ein?最小的假设函数g,但是这需要大量训练样本的支持,因为只有在训练样本数量N足够大时,才能使更复杂(即参数更多或者说VC维更大)的模型出现不好情况的几率变小,如上表的右列。






