[人工智能]激活函数详解

往期文章推荐：
? ? 脉冲神经网络资料汇总
? ?神经网络从入门到精通
? ?损失函数与代价函数

【版权申明】未经博主同意，谢绝转载！（请尊重原创，博主保留追究权）；

本博客的内容来自于：激活函数详解；

学习、合作与交流联系q384660495；

本博客的内容仅供学习与参考，并非营利；

一、什么是激活函数？

神经元通过树突从其他神经元中接受信号。树突的信号强度称为突触权值，用于与传入信号相乘。树突传出的信号在细胞体中累积，如果最后的信号强度超过了某个阈值，神经元就会允许轴突中的信息继续传递。否则，信号就会被阻止而得不到进一步的传播。激活函数决定了信号是否能够被通过。不过这个激活函数是极度简化的模型！具体可以参考我的这篇文章：

可以理解为在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数。可能是线性，可能是非线性，大部分是非线性关系。

好的激活函数的特征一般应当是平滑的，而且对于负值有较好的处理。

二、为什么需要激活函数？

如果不用激励函数，每一层节点的输入都是上层输出的线性函数。很容易验证，无论神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当。这种情况就是最原始的感知机（Perceptron）了，那么网络的逼近能力就相当有限。正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数）。如果没有非线性，神经网络就不能逼近XOR门。

若我们不经修改就输入到下一层神经元中，有可能演变成一个非常大的数从而使得计算过程非常难以处理。而激活函数的任务之一就是将神经元的输出映射到某个范围内。

俩个作用：一个是线性到非线性的转换，丰富函数的功能 ，第二个是控制输出范围

总而言之，不能在隐藏层用线性激活函数，可以用 ReLU 或者 tanh 或者 leaky ReLU 或 者其他的非线性激活函数，唯一可以用线性激活函数的通常就是输出层（回归问题）。

三、有哪些激活函数，都有什么性质和特点？

1、饱和激活函数

主要是Sigmoid、tanh函数和hard-Sigmoid函数。Sigmod和tanh都是饱和激活函数，即两者在输入值较大或较小的时候对输入值不再那么敏感，会饱和。

Sigmoid

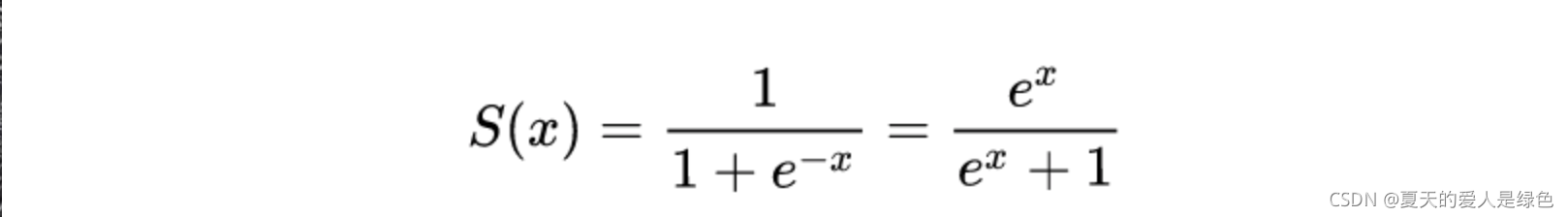
缺点有三个：
（1）趋近于0和趋近于1导数几乎为0.如果我们初始化神经网络的权值为 [ 0 , 1 ] [0,1] [0,1] 之间的随机值，由反向传播算法的数学推导可知，梯度从后向前传播时，每传递一层梯度值都会减小为原来的0.25倍，如果神经网络隐层特别多，那么梯度在穿过多层后将变得非常小接近于0，即出现梯度消失现象；当网络权值初始化为 ( 1 , + ∞ ) (1,+∞) (1,+∞) 区间内的值，则会出现梯度爆炸情况。
（2）非0均值。这样在反向传播的过程中w要么都往正方向更新，要么都往负方向更新，导致有一种捆绑的效果，使得收敛缓慢。
（3）其解析式中含有幂运算，计算机求解时相对来讲比较耗时

tanh

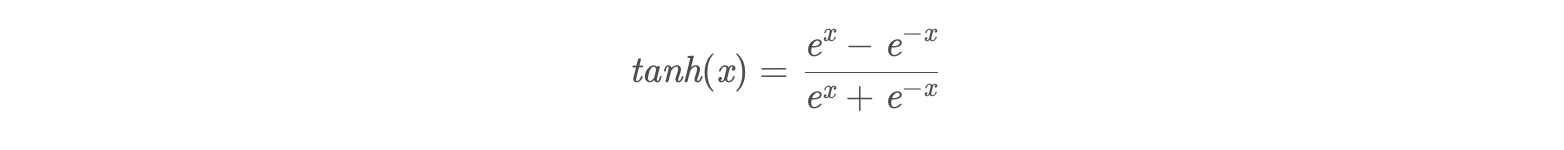
tanh读作Hyperbolic Tangent，它解决了Sigmoid函数的不是zero-centered输出问题，然而，梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。

梯度消失问题程度
tanh′(x)=1?tanh(x)²∈(0,1)
sigmoid: s′(x)=s(x)×(1?s(x))∈(0,1/4)
可以看出tanh(x)的梯度消失问题比sigmoid要轻.梯度如果过早消失,收敛速度较慢.

以零为中心的影响
如果当前参数(w0,w1)的最佳优化方向是(+d0, -d1),则根据反向传播计算公式,我们希望 x0 和 x1 符号相反。但是如果上一级神经元采用 Sigmoid 函数作为激活函数，sigmoid不以0为中心，输出值恒为正，那么我们无法进行最快的参数更新，而是走 Z 字形逼近最优解。

hard-Sigmoid

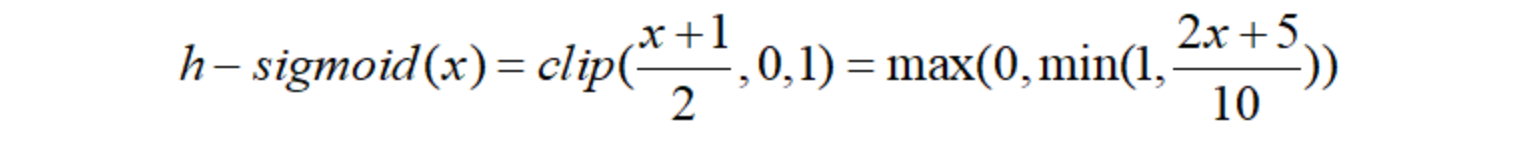
Sigmoid函数和hard-Sigmoid函数对比图：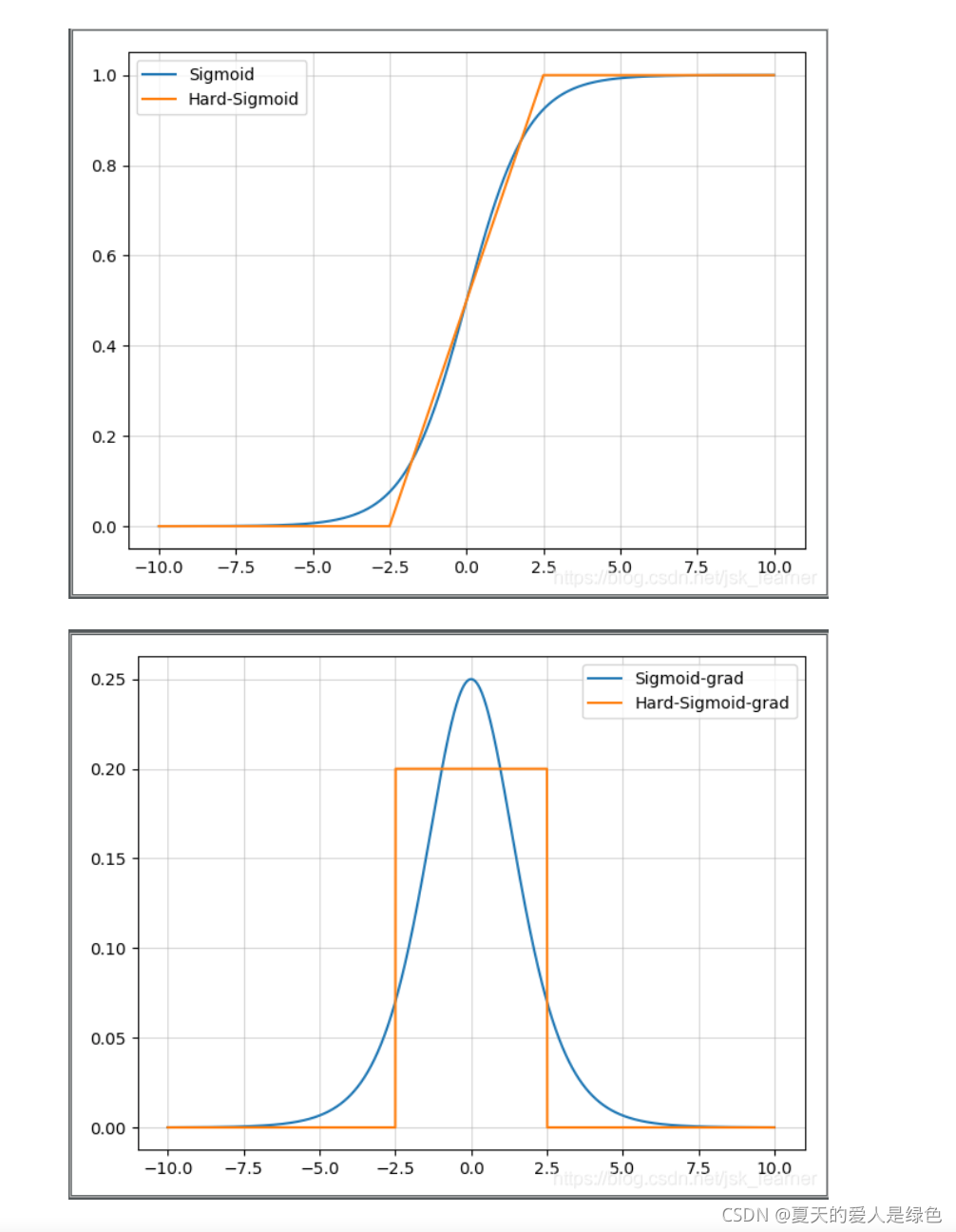
优点是没有幂运算，计算快，提高训练效率。缺点是就是首次派生值为零可能会导致神经元died或者过慢的学习率。

2、非饱和激活函数

而以Relu及其变体为代表的一类非饱和激活函数在防止梯度消失方面具有无可比拟的优势，即两者在输入值较大或较小的时候对输入值依然敏感，不会饱和，现如今基本很少在网络中使用Sigmod等饱和激活函数。

Relu（修正线性单元）

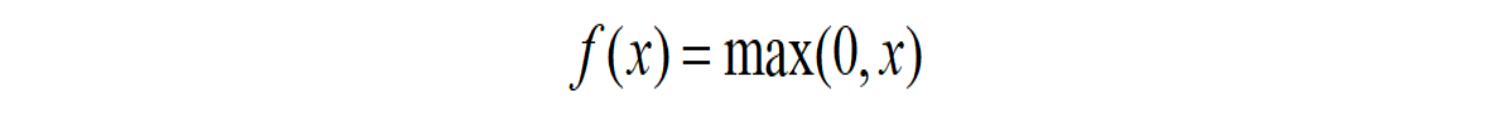
ReLU函数其实就是一个取最大值函数，注意这并不是全区间可导的，但是我们可以取sub-gradient，如上图所示。ReLU虽然简单，但却是近几年的重要成果，有以下几大优点：
1） 解决了gradient vanishing问题 (在正区间)
2）计算速度非常快，只需要判断输入是否大于0
3）收敛速度远快于sigmoid和tanh

ReLU也有几个需要特别注意的问题：
1）ReLU的输出不是zero-centered
2）Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。

有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。

解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

ELU（指数线性单元）

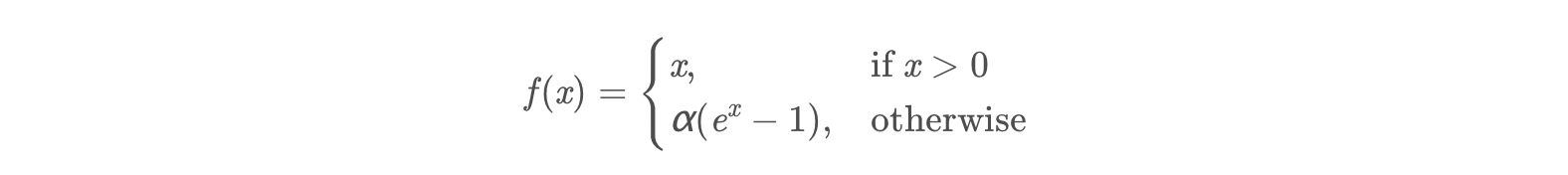
ELU也是为解决ReLU存在的问题而提出，显然，ELU有ReLU的基本所有优点，以及：

1. 不会有Dead ReLU问题
2. 输出的均值接近0，zero-centered

它的一个小问题在于计算量稍大。类似于Leaky ReLU，理论上虽然好于ReLU，但在实际使用中目前并没有好的证据ELU总是优于ReLU。

Leaky ReLU函数（PReLU）

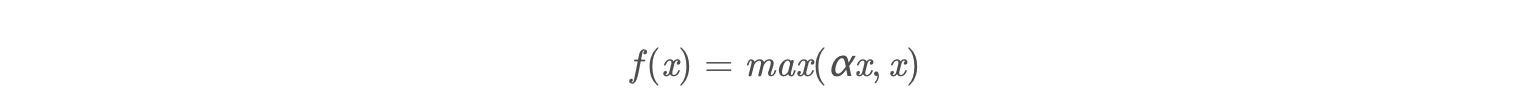
理论上来讲，Leaky ReLU有ReLU的所有优点，外加不会有Dead ReLU问题，但是在实际操作当中，并没有完全证明Leaky ReLU总是好于ReLU。

SELU

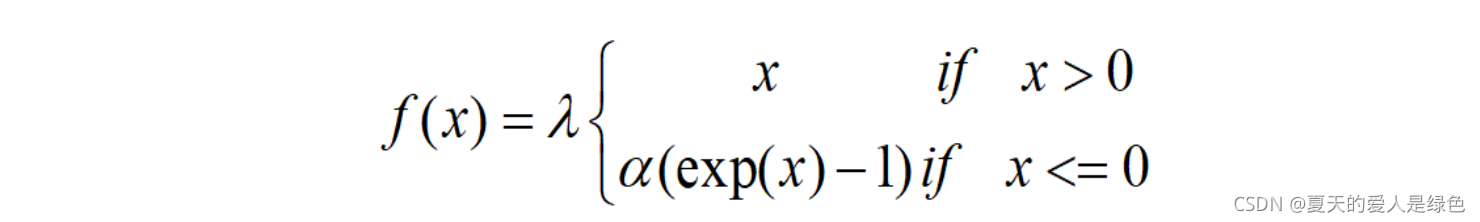
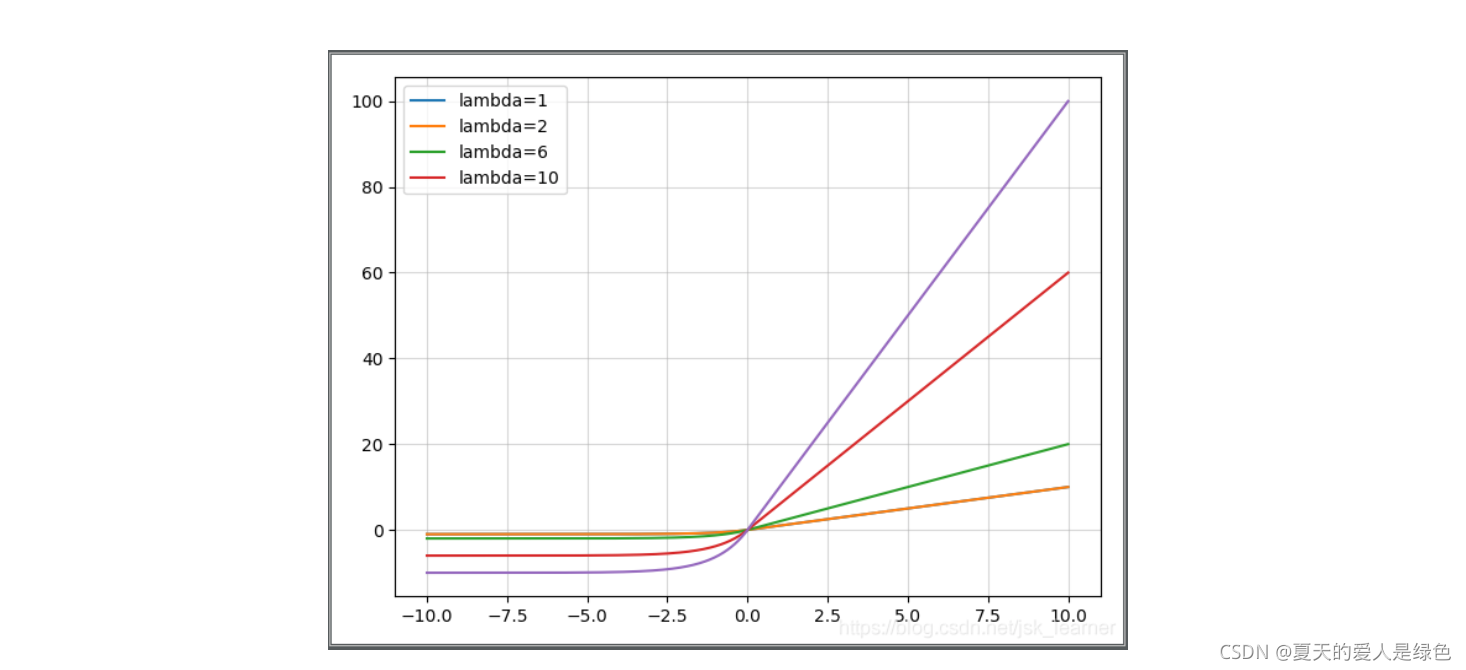
P-Relu（参数化修正线性单元）

R-Relu（随机纠正线性单元）

其他具体参考这篇文章：深度学习—激活函数详解

四、应用中如何选择合适的激活函数？

这个问题目前没有确定的方法。
1）深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。所以要尽量选择输出具有zero-centered特点的激活函数以加快模型的收敛速度。
2）如果使用 ReLU，那么一定要小心设置 learning rate，而且要注意不要让网络出现很多 “dead” 神经元，如果这个问题不好解决，那么可以试试 Leaky ReLU、PReLU 或者 Maxout.
3）最好不要用 sigmoid，你可以试试 tanh，不过可以预期它的效果会比不上 ReLU 和 Maxout.
4）除非在二分类问题中，否则请小心使用sigmoid函数。

代码实现

import matplotlib.pyplot as plt
import numpy as np

class ActivateFunc():
    def __init__(self, x, b=None, lamb=None, alpha=None, a=None):
        super(ActivateFunc, self).__init__()
        self.x = x
        self.b = b
        self.lamb = lamb
        self.alpha = alpha
        self.a = a

    def Sigmoid(self):
        y = np.exp(self.x) / (np.exp(self.x) + 1)
        y_grad = y*(1-y)
        return [y, y_grad]

    def Tanh(self):
        y = np.tanh(self.x)
        y_grad = 1 - y * y
        return [y, y_grad]

    def Swish(self): #b是一个常数，指定b
        y = self.x * (np.exp(self.b*self.x) / (np.exp(self.b*self.x) + 1))
        y_grad = np.exp(self.b*self.x)/(1+np.exp(self.b*self.x)) + self.x * (self.b*np.exp(self.b*self.x) / ((1+np.exp(self.b*self.x))*(1+np.exp(self.b*self.x))))
        return [y, y_grad]

    def ELU(self): # alpha是个常数，指定alpha
        y = np.where(self.x > 0, self.x, self.alpha * (np.exp(self.x) - 1))
        y_grad = np.where(self.x > 0, 1, self.alpha * np.exp(self.x))
        return [y, y_grad]

    def SELU(self):  # lamb大于1，指定lamb和alpha
        y = np.where(self.x > 0, self.lamb * self.x, self.lamb * self.alpha * (np.exp(self.x) - 1))
        y_grad = np.where(self.x > 0, self.lamb*1, self.lamb * self.alpha * np.exp(self.x))
        return [y, y_grad]

    def ReLU(self):
        y = np.where(self.x < 0, 0, self.x)
        y_grad = np.where(self.x < 0, 0, 1)
        return [y, y_grad]

    def PReLU(self):    # a大于1，指定a
        y = np.where(self.x < 0, self.x / self.a, self.x)
        y_grad = np.where(self.x < 0, 1 / self.a, 1)
        return [y, y_grad]

    def LeakyReLU(self):   # a大于1，指定a
        y = np.where(self.x < 0, self.x / self.a, self.x)
        y_grad = np.where(self.x < 0, 1 / self.a, 1)
        return [y, y_grad]

    def Mish(self):
        f = 1 + np.exp(x)
        y = self.x * ((f*f-1) / (f*f+1))
        y_grad = (f*f-1) / (f*f+1) + self.x*(4*f*(f-1)) / ((f*f+1)*(f*f+1))
        return [y, y_grad]

    def ReLU6(self):
        y = np.where(np.where(self.x < 0, 0, self.x) > 6, 6, np.where(self.x < 0, 0, self.x))
        y_grad = np.where(self.x > 6, 0, np.where(self.x < 0, 0, 1))
        return [y, y_grad]

    def Hard_Swish(self):
        f = self.x + 3
        relu6 = np.where(np.where(f < 0, 0, f) > 6, 6, np.where(f < 0, 0, f))
        relu6_grad = np.where(f > 6, 0, np.where(f < 0, 0, 1))
        y = self.x * relu6 / 6
        y_grad = relu6 / 6 + self.x * relu6_grad / 6
        return [y, y_grad]

    def Hard_Sigmoid(self):
        f = (2 * self.x + 5) / 10
        y = np.where(np.where(f > 1, 1, f) < 0, 0, np.where(f > 1, 1, f))
        y_grad = np.where(f > 0, np.where(f >= 1, 0, 1 / 5), 0)
        return [y, y_grad]


def PlotActiFunc(x, y, title):
    plt.grid(which='minor', alpha=0.2)
    plt.grid(which='major', alpha=0.5)
    plt.plot(x, y)
    plt.title(title)
    plt.show()

def PlotMultiFunc(x, y):
    plt.grid(which='minor', alpha=0.2)
    plt.grid(which='major', alpha=0.5)
    plt.plot(x, y)


if __name__ == '__main__':
    x = np.arange(-10, 10, 0.01)
    activateFunc = ActivateFunc(x)
    activateFunc.b = 1
    PlotActiFunc(x, activateFunc.Sigmoid()[0], title='Sigmoid')
    PlotActiFunc(x, activateFunc.Swish()[0], title='Swish')
    PlotActiFunc(x, activateFunc.ReLU()[0], title='ReLU')
    PlotActiFunc(x, activateFunc.Mish()[0], title='Mish')
    PlotActiFunc(x, activateFunc.Mish()[1], title='Mish-grad')
    PlotActiFunc(x, activateFunc.Swish()[1], title='Swish-grad')

    plt.figure(1)
    PlotMultiFunc(x, activateFunc.Mish()[1])
    PlotMultiFunc(x, activateFunc.Swish()[1])
    plt.legend(['Mish-grad', 'Swish-grad'])
    plt.figure(2)

    PlotMultiFunc(x, activateFunc.Swish()[0])
    PlotMultiFunc(x, activateFunc.Mish()[0])
    plt.legend(['Swish', 'Mish'])

    plt.figure(3)
    PlotMultiFunc(x, activateFunc.Swish()[0])
    PlotMultiFunc(x, activateFunc.Hard_Swish()[0])
    plt.legend(['Swish', 'Hard-Swish'])

    plt.figure(4)
    PlotMultiFunc(x, activateFunc.Sigmoid()[0])
    PlotMultiFunc(x, activateFunc.Hard_Sigmoid()[0])
    plt.legend(['Sigmoid', 'Hard-Sigmoid'])

    plt.figure(5)
    PlotMultiFunc(x, activateFunc.ReLU()[0])
    PlotMultiFunc(x, activateFunc.ReLU6()[0])
    plt.legend(['ReLU', 'ReLU6'])

    plt.figure(6)
    PlotMultiFunc(x, activateFunc.Swish()[1])
    PlotMultiFunc(x, activateFunc.Hard_Swish()[1])
    plt.legend(['Swish-grad', 'Hard-Swish-grad'])

    plt.figure(7)
    PlotMultiFunc(x, activateFunc.Sigmoid()[1])
    PlotMultiFunc(x, activateFunc.Hard_Sigmoid()[1])
    plt.legend(['Sigmoid-grad', 'Hard-Sigmoid-grad'])

    plt.figure(8)
    PlotMultiFunc(x, activateFunc.ReLU()[1])
    PlotMultiFunc(x, activateFunc.ReLU6()[1])
    plt.legend(['ReLU-grad', 'ReLU6-grad'])

    plt.show()

参考这篇文章：最全面：python绘制